论文笔记 ICNP 2016|MS-LSTM: a Multi-Scale LSTM Model for BGP Anomaly Detection
文章目录
-
- 1 简介
-
- 1.1 动机
- 1.2 创新
- 2 相关工作
- 3 方法
-
- 3.1 预处理
- 3.2 MS_LSTM
- 4 实验
- 5 总结
1 简介
论文题目:MS-LSTM: a Multi-Scale LSTM Model for BGP Anomaly Detection
论文来源:ICNP 2016
论文链接:https://ieeexplore.ieee.org/abstract/document/7785326
1.1 动机
- 无论流量数据的时间序列如何,目前的方法通常都选择当前的流量特征来做出决策,其中时间序列分析可以为识别状态变化带来额外的重要信息。
- 基于统计的方法假设数据集遵循一定的分布,并且需要领域知识,例如阈值参数。
1.2 创新
- 提出MS-LSTM(multi-scale LSTM)用于BGP异常检测。
- 通过实验证明,在现有的模型中最佳的时间尺度,可以在BGP异常检测上提升大约10%的表现。
2 相关工作
- 基于模式的方法:异常被识别为基础分布中发生的相关突然变化。
- 基于规则的方法:使用IRF(Internet Routing Forensics),缺点是需要先验知识和大量的计算。
- 基于机器学习的方法: 它们均独立地看待输入序列,没有考虑流量数据的序列性。而流量数据是多变量时间序列,异常形式随时间信息逐渐变化。
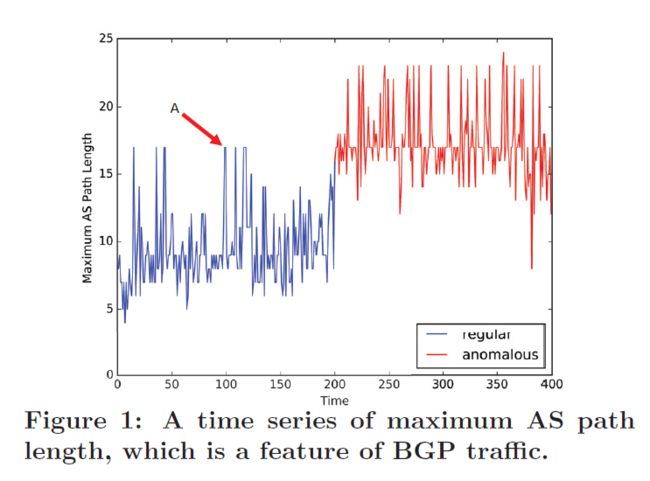
将历史信息整合到分类器中可以使决策更加谨慎和准确。与大多数其他时间序列一样,互联网流量具有多尺度属性。 意味着在不同的时间尺度上,序列可以表现出不同的模式。如下图,可以发现在更大的时间尺度上,时间序列的全局趋势更容易捕捉,但更难感知局部变化。
3 方法
3.1 预处理
设BGP流量数据是一个在一分钟的时间间隔中收集的n个时间点的时间序 x t 1 , x t 2 , . . . , x t n x_{t_1},x_{t_2},...,x_{t_n} xt1,xt2,...,xtn,为33维向量(抽取流量的33个特征)。设窗口的大小为e, x t n x_{t_n} xtn的状态与 S n = ( s t n − e − + 1 , s t n − e − + 2 , . . . , s t n ) S_n=(s_{t_{n-e-+1}},s_{t_{n-e-+2}},...,s_{t_{n}}) Sn=(stn−e−+1,stn−e−+2,...,stn)有关。每个子序列 S n S_n Sn被时间尺度d压缩(如 d 1 = 1 / p ( x t n − e + 1 + x t n − e + 2 + . . . x t n − e + p ) d_1=1/p(x_{t_{n-e+1}}+x_{t_{n-e+2}}+...x_{t_{n-e+p}}) d1=1/p(xtn−e+1+xtn−e+2+...xtn−e+p))。通过这种方式,可以从训练数据S中得到n-e+1个集合。每一个集合的标签与最后一个状态的向量相同, L ( S n ) = L ( x t n ) L(S_n)=L(x_{t_n}) L(Sn)=L(xtn)
3.2 MS_LSTM
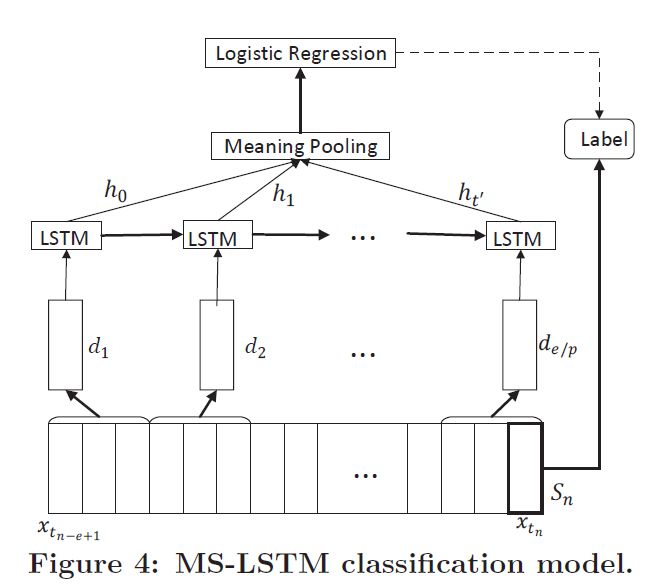
模型的整体结构如下,LSTM输出值 h 1 , h 2 , . . . , h t ′ h_1,h_2,...,h_t' h1,h2,...,ht′被平均池化层平均,得到h。逻辑回归层是一个二分类器,训练h和标签的损失。
4 实验
使用SVM、Naive Bayes Classifier和Boosting modules作为baseline,实验结果如下,可以发现通过增加序列窗口可以提高全部分类方法大约10%的准确率。
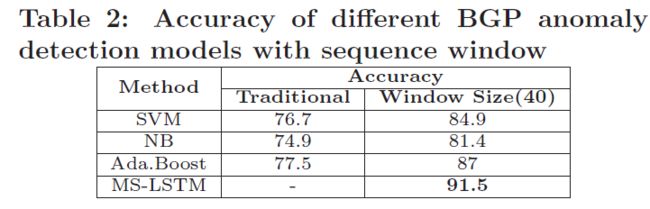
不同窗口大小的实验结果如下,可以发现随着窗口大小的增加,全部方法的准确率先增加再减小,最佳大小为40.
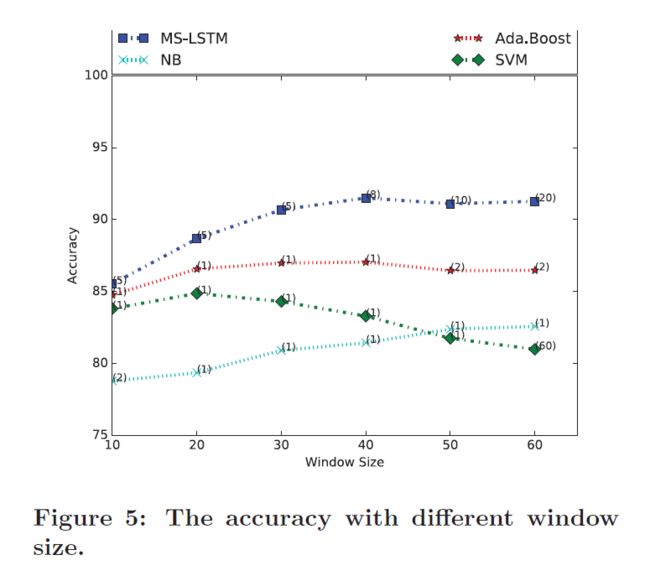
不同时间尺度的实验如下,可以发现MS-LSTM在时间尺度为8是达到最佳的效果。
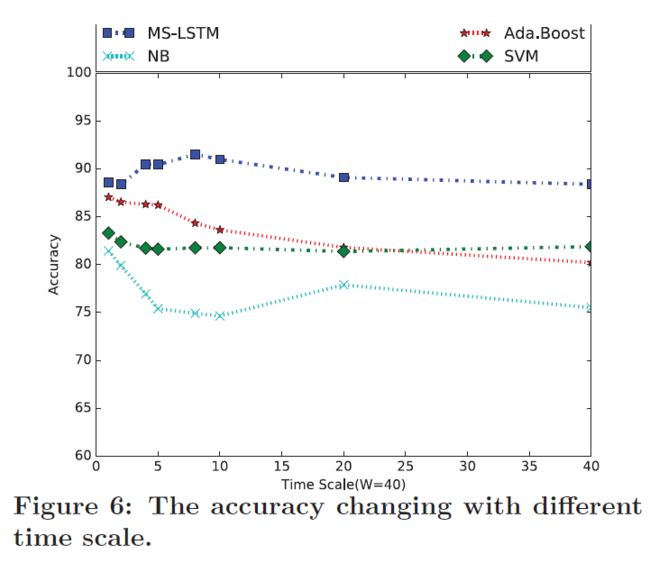
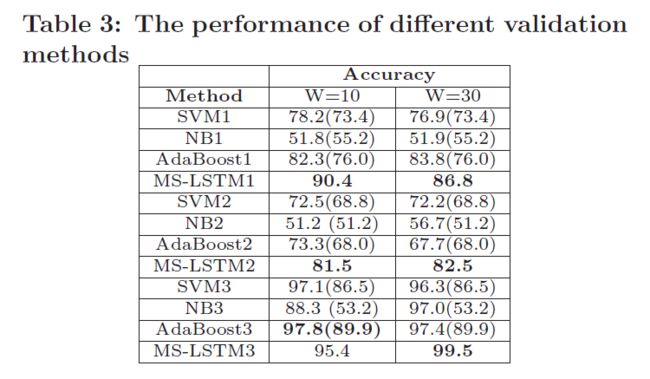
交叉验证的实验结果如下,使用三种数据,其中两种数据训练,其余一种数据测试,共三种方法。
通过下图比较预测结果与真实标签,与Naive Bayes Classifie和SVM相比,MS-LSTM模型没有误报,可以检测到大多数异常样本。
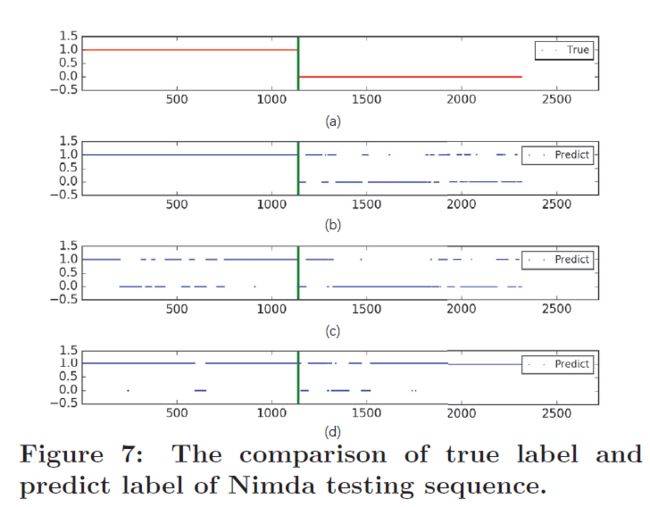
5 总结
- 提出多尺度LSTM模型(MS-LSTM),用于检测几个典型的现实世界事件的 BGP 异常,模型可以达到更高的准确率和更低的误报率。
- MS-LSTM 可以在具有最佳时间尺度的时间模式中学习长期依赖。同时发现时间尺度的选择影响大部分用于BGP异常检测的分类模型的表现。
h t = f ( x t , h t − 1 ; θ ) h_t=f(x_t,h_{t-1};\theta) ht=f(xt,ht−1;θ)
d h t d θ = ∂ h t ∂ h t − 1 d h t − 1 d θ + ∂ h t ∂ θ \frac {dh_t}{d_{\theta}}=\frac { {\partial}h_t}{ {\partial}h_{t-1}}\frac {dh_{t-1}}{d\theta}+\frac{ {\partial}h_t}{ {\partial}{\theta}} dθdht=∂ht−1∂htdθdht−1+∂θ∂ht
BGP流量数据: x t 1 , x t 2 , . . . , x t n x_{t_1},x_{t_2},...,x_{t_n} xt1,xt2,...,xtn
设置窗口大小为e,使用 x n − e + 1 x_{n-e+1} xn−e+1到 x t n x_{t_n} xtn数据的特征信息预测 x t n x_{t_n} xtn
S n = x t n − e + 1 , x t n − e + 2 , . . . , x t n S_n={x_{t_{n-e+1}},x_{t_{n-e+2}},...,x_{t_{n}}} Sn=xtn−e+1,xtn−e+2,...,xtn
S n = ( d 1 , d 2 , . . . , d e / p ) S_n=(d_1,d_2,...,d_{e/p}) Sn=(d1,d2,...,de/p)
d 1 = 1 / p ( x t n − e + 1 + x t n − e + 2 + . . . x t n − e + p ) d_1=1/p(x_{t_{n-e+1}}+x_{t_{n-e+2}}+...x_{t_{n-e+p}}) d1=1/p(xtn−e+1+xtn−e+2+...xtn−e+p)
h 0 , h 1 . . . h t ′ = L S T M ( d 1 , d 2 , . . . , d e / p ) {h_0,h_1...h_{t'}}=LSTM(d_1,d_2,...,d_{e/p}) h0,h1...ht′=LSTM(d1,d2,...,de/p)
h = p e ( h 0 , h 1 . . . h t ′ ) h = \frac pe (h_0,h_1...h_{t'}) h=ep(h0,h1...ht′)
p = f θ ( h ) p = f_{\theta}(h) p=fθ(h)