健浩

5 机器学习朴素贝叶斯算法高斯模型多项式模型伯努利模型拉普拉普平滑系数 TfidfVectorizer

机器学习

1 朴素贝叶斯算法

1.1 朴素贝叶斯算法介绍

朴素贝叶斯算法是一种衡量标签和特征之间概率关系的监督学习算法，是一种专注于分类的算法。“朴素”二字表示这个算法基于一个朴素的假设，即样本中所有的特征都相互独立。

朴素贝叶斯法（Naive Bayes）是基于贝叶斯定理与特征独立假设的分类方法。对于给定的训练数据集，首先基于特征独立假设建立输入/输出的联合概率分布模型，然后基于此模型，对于给定的输入x，利用贝叶斯定理计算出后验概率最大的输出y。

1.1.1 贝叶斯公式

贝叶斯公式是关于随机事件A和B的条件概率和边缘概率的公式。
$\over {P(A) }}$

1.1.2 基于贝叶斯算法构建分类模型

对公式进行修改
将事件A替换成“特征”，表示样本具有指定特征的事件；
将事件B替换成“标签”，表示样本被划分到指定标签的事件。

$\over P(特征) }$
$\begin{aligned} P(标签|特征1，特征2，特征3...) =& { { P(特征1，特征2，特征3...|标签) P(标签) } \over P(特征) } \\[5ex] P(标签|特征1，特征2，特征3...) =& { { [P(特征1|标签) P(特征2|标签) P(特征3|标签)...] P(标签) } \over P(特征) } \end{aligned}$

准备工作：
样本具有各个特征的概率 P(特征)；
样本被划分到不同标签类别中的概率 P(标签)；
被划分到指定标签下的样本身上具有各个特征的概率 P(特征|标签) ，也可以理解为一个样本被划分到指定标签的条件下，这个样本具有指定特征的概率 P(特征|标签)。

建立模型：
对于样本被划分到指定标签这一事件，分类结果是在样本所携带的多个特征共同作用下完成的，根据贝叶斯公式计算出样本在每个特征单独作用下被划分到不同标签类别中的后验概率 P(标签|特征)。

使用模型：
输入具有某些特征的未知样本，模型分别会计算出在特征作用下未知样本被划分到各个类别中的后验概率。
贝叶斯分类器的决策思想是选择最高概率对应的标签作为分类结果。

1.1.3 名词解释

先验概率
先验概率是指事件发生前的预判概率，多维随机变量中先验概率指的是各个变量的边缘概率，即上面的 P(特征) 和 P(标签)。
条件概率(似然)
一个事件已经发生的条件下另一个事件发生的概率，即上面的 P(标签|特征) 和 P(特征|标签)。
后验概率
在样本具有某些特征的条件下，样本被划分到指定标签这一事件发生的条件概率，即上面的 P(标签|特征)。

贝叶斯定理也可以理解为通过先验概率和条件概率计算后验概率的定理。

1.1.4 举例说明

某中学中男生占60%，女生占40%，所有男生都穿长裤，女生中一半穿长裤一半穿裙子，随机选取一名穿长裤的学生，推断这名学生的性别。

解决思路

通过问题确定特征和标签，穿长裤/穿裙子是特征，男生类别/女生类别是标签；
确定目标
随机找到一个具有穿长裤特征的学生，分别计算出这名学生被划分到男生标签/女生标签的概率 P(标签|特征)。
计算先验概率 P(特征)、P(标签) 和条件概率 P(特征|标签)。

计算先验概率 P(标签)
中学中男生占60%，女生占40%。

P(男生标签) = 60% = 0.6
P(女生标签) = 40% = 0.4

计算先验概率 P(特征)
假设有10个学生，按男女比例划分为6个男生，4个女生。

P(穿长裤特征) = (6 + 4/2) / 10 = 0.8
P(穿裙子特征) = (4/2) / 10 = 0.2

计算条件概率 P(特征|标签)

# 所有男生都穿长裤。
P(穿长裤特征|男生标签) = 1.0
P(穿裙子特征|男生标签) = 0.0

# 女生中一半穿长裤一半穿裙子。
P(穿长裤特征|女生标签) = 0.5
P(穿裙子特征|女生标签) = 0.5

最后利用贝叶斯定理计算后验概率 P(标签|特征)

# 随机选取一名穿长裤的学生，分别计算出这名学生是男生/女生的概率 
P(男生标签/女生标签|穿长裤特征)

$\begin{aligned} P(男生标签|穿长裤特征) =& { { P(穿长裤特征|男生标签) P(男生标签) } \over P(穿长裤特征)} \\[5ex] P(男生标签|穿长裤特征) =& {1.0 \times 0.6 \over 0.8} = 0.75 \\[5ex] P(女生标签|穿长裤特征) =& { { P(穿长裤特征|女生标签) P(女生标签) } \over P(穿长裤特征)} \\[5ex] P(女生标签|穿长裤特征) =& {0.5 \times 0.4 \over 0.8} = 0.25 \end{aligned}$

结论
模型会根据所有标签的后验概率中的最高值做出决策，将具有穿长裤特征的学生样本划分到男生标签中。

2 贝叶斯算法模型

贝叶斯定理将参数的先验概率与后验概率通过似然联系在一起。
贝叶斯算法模型将参数视为变量，服从一定的分布。构建贝叶斯算法模型本质上是使用极大似然法估算模型参数，即计算出后验概率最大时的模型参数。

sklearn中提供了三类贝叶斯算法模型，分别是高斯模型、多项式模型和伯努利模型。

2.1 高斯模型

2.1.1 高斯分布

高斯分布(Gaussian distribution)，也称为正态分布(Normal distribution)，是一种连续型随机变量的概率分布。
对于随机变量 $X$ ，若 $X$ 服从数学期望为 $μ$ 、方差为 $σ^2$ 的正态分布，记为 $\sim N(μ, σ^2)$ 。

一维随机变量 $\sim N(μ, σ^2)$ ，概率密度函数表示为
$\over {\sqrt {2\pi} σ}}e^{-{(x-μ)^2 \over 2σ^2}}$

中心极限定理指出，如果样本量足够大，则变量均值的采样分布将近似于高斯分布，与该变量在总体中的分布无关。

随机事件发生的概率在整体上服从高斯分布。
以连续抛硬币为例，硬币出现正面记1分，出现反面记-1分，以连续抛10次硬币为一组并记录得分，经过大量重复试验后得到的分数统计结果为：

2.1.2 高斯模型

高斯模型用于处理特征是连续型的分类问题。
使用高斯模型的前提是假设先验概率 P(特征|标签) 服从高斯分布：

$P(x_i|Y)=f(x_i; μ_y, σ_y) \varepsilon = {1 \over {\sqrt {2\pi} σ_y}}e^{-{(x_i-μ_y)^2 \over 2σ_y^2}}$

先验概率
对于类别的先验概率 $P(y_j)$ ，可以通过参数priors手动指定，不指定时默认值是 $P(y_j)={m_j \over m}$ ，其中 $m_j$ 表示标签 $y_j$ 的训练集样本数，m表示训练集样本总数。
构造高斯模型
基于训练集数据，利用属于每个标签 $y_j$ 的样本数据集 $X_{y_j}$ ，计算出属于这个标签的数据均值 $\mu_{y_j}$ 和标准差 $\sigma_{y_j}$ 。
对测试集进行分类
对于测试集数据，利用高斯模型计算出样本在每个特征 $x_i$ 作用下被划分到各个标签 $y_j$ 的概率 $P(x_i|y_j)$ 。
例如，判断一个人是美还是丑，则美还是丑就是分类标签，这里用于分类的特征包括身高、体重和三围。
对于每一组数据，高斯模型会分别计算出身高/体重/三围特征在美/丑标签中的条件概率，即 P(身高|美)、P(身高|丑)、P(体重|美)、P(体重|丑)、P(三围|美)、P(三围|丑)。
极大似然估计
将各个标签下每个特征的条件概率相乘得到这个标签的似然度。
用先验概率乘以指定标签的似然度再进行归一化处理，得到这个样本数据属于这个标签下的概率，其中概率最大值对应的标签就被视为输入样本所属的类别。

2.1.3 iris案例

import sklearn.datasets as datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
feature = iris.data
target = iris.target

x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2020)

g = GaussianNB()
g.fit(x_train, y_train)

查看iris分类结果

g.score(x_test, y_test)  # 0.8333333333333334

# 利用高斯模型对第一个测试样本进行分类，获得属于各个类别的概率。
g.predict(x_test[0].reshape((1, -1)))
'''
array([[7.21319207e-239, 3.44645792e-009, 9.99999997e-001]])
'''

# 对获得的概率进行了对数转换。
g.predict_log_proba(x_test[0].reshape((1, -1)))
'''
array([[-5.48341926e+02, -1.94859188e+01, -3.44645801e-09]])
'''

结论，这条样本数据x_test[0]的最大概率为9.99999997e-001(或者经过对数处理为-3.44645801e-09)，对应的标签是类别三。

2.1.4 手写数字识别案例

准备数据

import sklearn.datasets as datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

digist = datasets.load_digits()
feature = digist.data
target = digist.target
feature.shape  # (1797, 64)
# 64列说明图片是8*8像素。

x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.1, random_state=2020)

训练模型

g = GaussianNB()
g.fit(x_train, y_train)

评估模型

g.score(x_test, y_test)  # 0.8333333333333334

y_pred = g.predict(x_test)
print('模型分类结果:', y_pred[:10])
print('实际样本标签:', y_test[:10])
'''
模型分类结果: [4 3 6 4 8 7 2 8 1 1]
实际样本标签: [4 3 6 4 8 7 2 2 1 2]
'''

y_test[3]  # 4
g.predict_log_proba(x_test[3].reshape(1, -1))
'''
array([[-1.42975581e+03, -2.33112575e+01, -2.21201344e+02,
        -5.00236423e+02, -1.54472863e-05, -6.20715298e+01,
        -5.74683561e+02, -1.10780898e+01, -7.29616360e+01,
        -8.69033822e+01]])
'''

g.predict_log_proba(x_test[3].reshape(1, -1)).max()  # -1.5447286294545393e-05

对于指定样本x_test[3]，最大概率为-1.54472863e-05，对应的数字标签是4。

2.2 多项式模型

2.2.1 介绍

多项式模型主要用于离散型特征的概率计算，例如文章类型分类。如果需要处理连续型特征的问题，推荐使用高斯模型。
注意，sklearn的多项式模型不接受输入负值。

2.2.2 原理介绍

以文章类型分类为例，目标是通过文章词汇统计计算出一篇文章属于各个类别的概率，即计算条件概率 P(类别|文章词汇)。

P(体育|词1，词2，词3...) = 1/6
P(财经|词1，词2，词3...) = 1/3

此处的条件概率是多条件下的条件概率，计算多条件下的条件概率需要将其转化为各个单条件的条件概率。

利用贝叶斯公式
$\begin{aligned} P(C|W)=&{ {P(W|C)P(C)} \over {P(W)}} \\[5ex] P(C|F_1, F_2,...)=&{ {P(F_1, F_2,...|C)P(C)} \over {P(F_1, F_2,...)}} \end{aligned}$

其中， $W$ 为文档的特征，由不同的词汇特征 $F_1, F_2,...$ 组成， $C$ 为文档的标签类别。

接下来就是计算 $P (C)$ 和 $P(F_1, F_2,...|C)P(C)$

$P (C)$ 表示各个标签的边缘概率(先验概率)，等于训练集中指定标签类别的文章数量除以总文章数量；
$P(F_1|C)$ 表示指定类别的文章中指定词汇出现的条件概率，等于词汇 $F_1$ 在类别 $C$ 下所有文章中出现的次数除以类别 $C$ 下所有文章的词汇总数。

2.2.3 拉普拉普平滑系数

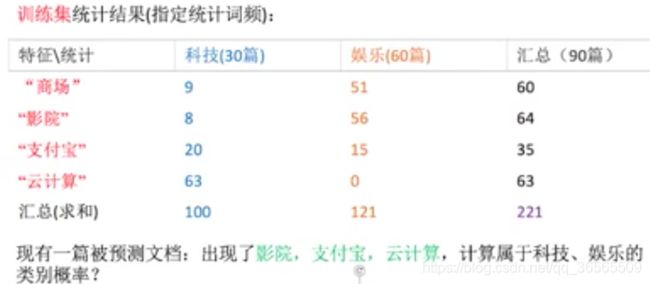
训练集中共有90篇文章，其中包括30篇科技文章和60篇娱乐文章。
特征词汇包括商场，影院，支付宝和云计算。

计算 $P(F_1, F_2,...|C)P(C)$

科技
$\over 100}\times{20 \over 100}\times{63 \over 100}\times{30 \over 90} = 0.00456109$

娱乐
$\over 121}\times{15 \over 121}\times{0 \over 121}\times{60 \over 90} = 0$

$P (影院, 支付宝, 云计算 ∣ 娱乐) = 0$ ，这是由于词汇云计算在娱乐类型的文章中出现的次数为0，显然不符合常理。

拉普拉普平滑系数
使用拉普拉普平滑系数可以处理由于某个特征词汇的统计量为0导致的整体概率为0的问题。

${N_i + \alpha} \over {N + \alpha m}}$
其中 $\alpha$ 表示系数，一般指定为1，m为训练文档中统计出的特征词数量。

2.2.4 文本特征抽取 - TfidfVectorizer

TF-IDF概念
在信息检索中，tf-idf (词频-逆文档频率)是一种统计方法，用以评估一个单词在一篇文档集合或语料库中的重要程度。

原理
TF-IDF实际上是TF * IDF，如果某个词汇或短语在一篇文章中出现的频率高(即TF高)，在其它文章中却很少出现(即IDF高)，那么认为这个词汇或短语具有很好的类别区分能力，适合用来作分类特征。

TF
TF表示某个给定的词汇t在一篇指定文档d中出现的频率。
如果TF越高，则表示词汇t对文档d的重要程度越高，如果TF越低，则表示词汇t对文档d的重要程度越低。
是否可以使用TF作为文本相似度的评价标准呢？
答案是不行的，举个例子，“我”、“了”、“是”等常用的中文词汇在每篇文档中都可能具有非常高的词频，如果使用TF作为文本相似度的评价标准，那么几乎每篇文档都能被命中。
$\begin{aligned} TF(w) =& {词汇w在文档中出现的次数 \over 文档词汇总数} \\[5ex] TF(w) =& P(F1|C) = {N_i \over N} \end{aligned}$
IDF
IDF是指逆向文章频率。某些词汇在文本中可能频繁地出现，但实际上并不重要，即信息量小，例如is、of、that等英文单词或者“我”、“了”、“是”等中文词汇，这些词汇在语料库中出现的频率非常大，可以利用这个特点降低其权重。

2.2.5 文档分类案例

20 newsgroups数据集包含约18000篇新闻文章，共涉及20种话题。

导入数据

import sklearn.datasets as datasets
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB

news = datasets.fetch_20newsgroups(data_home='./')

feature = news.data
# 返回列表，元素为每一篇文章。
len(feature)  # 11314

target = news.target
# 返回列表ndarray，元素为每一篇文章的类别。

特征抽取

t = TfidfVectorizer()
feature_t = t.fit_transform(feature)
# 返回Sparse矩阵，表示特征词汇位置以及TF。
'''
(0, 86580)	0.13157118714240987
(0, 128420)	0.04278499079283093
(0, 35983)	0.03770448563619875
(0, 35187)	0.09353930598317124
(0, 66098)	0.09785515708314481
...
'''

print(t.get_feature_names())  # 查看特征

拆分数据集

x_train, x_test, y_train, y_test = train_test_split(feature_t, target, test_size=0.01, random_state=2020)