河南省第十三届ICPC大学生程序设计竞赛 题解

河南省第十三届ICPC大学生程序设计竞赛 题解

难的题挺难，简单的也很简单。总体而言题目质量还可以，有许多很新奇的知识点插入。

A. 祝融传火

题目给定$n\ast m$矩阵以及长宽为$h,w$的矩形，问是否存在$A[x][y],A[x+H-1][y],A[x][y+W-1],A[x+H-1][y+W-1]$四个点相等的情况。

签到题，直接暴力判断。

#include 
using namespace std;

const int N = 1010;
int a[N][N];
int n, m;

inline bool judge(int x, int y){
     
    if(x < n && y < m) return true;
    else return false;
}

signed main(){
     
    cin >> n >> m;
    for(int i = 0; i < n; i++){
     
        for(int j = 0; j < m; j++) cin >> a[i][j];
    }
    int h, w; cin >> h >> w;
    for(int i = 0; i < n; i++){
     
        for(int j = 0; j < m; j++){
     
            if(judge(i + h - 1, j) && judge(i,j + w - 1)){
     
                if(a[i][j] == a[i + h - 1][j] && a[i][j] == a[i][j + w - 1] && a[i][j] == a[i + h - 1][j + w - 1]){
     
                    return cout << "YES" << endl, 0;
                }
            }
        }
    }
    cout << "NO" << endl;
    return 0;
}

B. Honrycomb

思维+构造+最短路

构造是指构造坐标系：以$1$为原点，$6,3$号格子为$x$轴方向，$4,7$号格子为$y$轴方向。

对于输入中的格子编号同样可以转化为坐标：不难发现格子的编号逐圈扩大，第$0$圈大小为$1$，第$i$圈的大小为$6i$；因此对于编号为$x$的格子，我们可以找到一个$k$使得$1+6\ast \frac{(k\ast (k-1))}{2}<x\le 1+6\ast \frac{(k\ast (k+1))}{2}$，则格子位于第$k$圈。

我们固定一个点用于追溯其他点的坐标:$(0,k)$，其编号必为$1+6\ast \frac{(k\ast (k+1))}{2}$，可根据这个格子推出其他格子的坐标。

但需要注意的是，此时合法的走法不仅仅是上下左右，还包括一个斜对角方向$(+1,+1)、(-1,-1)$

于是问题就是一个单纯的最短路问题了，$SPFA$或者$Dijkstra$跑一下即可出答案。

代码待补。。。

C. Alice and Bob

思路还不明确 待补。

目测是个二分。

D. Connie

期望DP+KMP匹配

求期望的方法：$\frac{总权值}{总方案数}$

构造方法还在思考，思路不太明确。

E. Dance with a stick

一点思路也没有，然后队友操作了一波，让我当场想转行学高数…

本题与风车问题几乎一致(IMO中某题)：

• 偶数点必无解
• 奇数个点时：所有点按$x$坐标从小到大排序(若$x$坐标相同则按$y$坐标从小到大排序)。选择排在中间的点，同时做向量$(-1，1000000000)$

如何证明正确性？

1. 这条直线只过一点
2. 这条直线左右两边的点数都相同
3. 在转动直线的过程中，直线左右两侧的点数量均不变(枚举数据发现)

向量旋转$180^{。}$后斜率不变，仍然满足直线两侧点数相同，必回到起始位置。

#include 
using namespace std;

struct node{
     
    int x, y;
    const bool operator<(const node u) const{
      return x < u.x || x == u.x && y < u.y; }
} point[100005];
signed main(){
     
    int n; cin >> n;
    for (int i = 0; i < n; i++) cin >> point[i].x >> point[i].y;
    sort(point, point + n);
    if (n & 1){
     
        cout << "Yes" << endl;
        cout << point[n / 2].x << " " << point[n / 2].y << " " << -1 << " " << 1000000000;
    }
    else{
     
        cout << "No";
    }
    return 0;
}

F.图像识别

找出$\#$和左边原点，签到题

#include 
using namespace std;

char s[1005][1005];

signed main(){
     
    ios_base::sync_with_stdio(false);
    int n, m; cin >> n >> m;
    int tarx, tary;
    for(int i = 1; i <= n; i++){
     
        for(int j = 1; j <= m; j++){
     
            char tmp; cin >> tmp;
            if(tmp == '#') tarx = i, tary = j;
            else s[i][j] = tmp;
        }
    }
    int sx, sy;
    for(int i = 1; i <= m; i++) s[0][i] = s[n+1][i] = '*';
    for(int i = 1; i <= n; i++) s[i][0] = s[i][m+1] = '*';
    for(int i = 1; i <= n; i++){
     
        for(int j=1;j<=m;j++){
     
            if(s[i - 1][j] == '*'&& s[i][j] == '*' &&s[i + 1][j] == '*' && s[i][j-1] == '*' && s[i][j + 1] == '*') sx = i, sy = j;
        }
    }
    cout << tary - sy << ' ' << tarx - sx << endl;
    return 0;
}

G. Elo mountains

AC自动机+构造

蒟蒻啥也不会，先学完再说吧。。。

H. 焦糖布丁

树上阶梯博弈，将根节点深度定位$0$，当且仅当深度为奇数的节点上的发票数量异或和为$0$，先手必败

构造树的方法：构造一棵两层树，第一层深度均为$1$，第二层深度均为$2$，则转化为$NIM$博弈若第一层节点异或和为$0$则先手必败。

需要用线性基构造一组异或和为$0$的子集。

代码待补。线性基学也罢了。

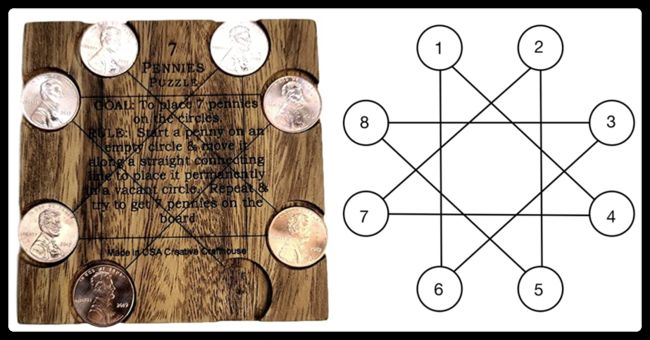
I. 七便士

按照上图的顺序给定每个点硬币的状态(残局)。

方盘上有八个圆坑，每个圆坑能正好放置一枚便士，每个圆坑与其他另外两个圆坑相连（图中黑线）；
• 每次操作分为两部分：（每次操作两部分缺一不可）

1. ​ 将一枚便士放置于一个尚未放置便士的圆坑中；
2. ​ 再将该便士沿着黑线移动至另一尚未放置便士的圆坑中；

问能否解出给定的七便士残局。

基本思路：观察上图具有鲜明的特征：每个点均具有两条边连接。那么可以指定一个遍历顺序$\{1,4,7,2,5,8,3,6\}$。

如果当前点能够被硬币塞上，那么当前点以及上一个点一定是空的；因此我们只需要统计原先$1$的个数，然后统计连续同时为零的元素的个数，如果这个Puzzle能够被解出来，那么总个数为$7$(因为每次比较的是两个相邻元素)。此时刚好剩下一个空位。

#include 
using namespace std;

const int ser[] = {
     0, 1, 4, 7, 2, 5, 8, 3, 6};
char a[9];

int main(){
     
    int t = 0; cin >> t;
    while(t--){
     
        int cnt = 0;
        for(int i = 1; i <= 8; i++) cin >> a[i];
        for(int i = 1; i <= 8; i++)
            if(a[i] == '1') cnt++;
        if(a[ser[8]] == '0' && a[ser[1]] == '0' && cnt != 0) cnt++;
        for(int i = 1; i < 8; i++){
     
            if(a[ser[i]] == '0' && a[ser[i + 1]] == '0') cnt++;
        }
        if(cnt == 7) cout << "Yes" << endl;
        else cout << "No" << endl;
    } 
    return 0;
}

J. 甜甜圈

每次找到权值最大的点并删点求距离，直接模拟在$1e5$的数据量下会爆，因此考虑使用高效的数据结构对移动进行维护。

我们采用两堆甜甜圈顶对顶的储存方式，这样在移动过程中的移动次数可以直接通过坐标相减求得。

首先对于每个点，我们需要保存 ①.甜度值 ②.原次序 ③.当前点之前还有多少个点

然后我们就可以根据甜度值对点进行排序。

我们模拟一个隔板，位于下标$i$时表示隔板位于$i$和$i+1$之间，其初始值为$n$，我们每次取出最大的数与隔板位置(除首次外，均为上次的最大点坐标)，查询两点之前还有多少个点并作差累加到答案上，同时删除当前最大点。遍历完后便可得出答案。

#include 
#define lowbit(x) ((x) & (-x))
using namespace std;

struct node{
      
    int x, y; 
    const int operator< (node a) const {
      return y > a.y; }
};

const int N = 100000 + 10;
node a[N];
int tree[N], len;

inline void add(int x, int k){
     
    while(x <= len){
     
        tree[x] = tree[x] + k;
        x = x + lowbit(x);
    }
}

inline int getsum(int x){
     
    int ans = 0;
    while(x >= 1){
     
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}

int main(){
     
    ios_base::sync_with_stdio(false);
    int n, m,ans = 0; cin >> n >> m; len = n + m;
    for(int i = n; i > 0; i--){
     
        add(i, 1);
        cin >> a[i].y;
        a[i].x = i;
    }
    for(int i = n + 1; i <= n + m; i++){
     
        add(i, 1);
        cin >> a[i].y;
        a[i].x = i;
    }
    a[0].x = n;
    sort(a + 1, a + n + m + 1);
    for(int i = 1; i <= n + m; i++){
     
        add(a[i].x, -1);
        ans += abs(getsum(a[i].x) - getsum(a[i - 1].x));
    }
    cout << ans << endl;
    return 0;
}

K.残局

听说 是对抗搜索？

没有任何思路。。。

L.手动计算

高数题，听说可以用格林公式和辛普森公式解，然而并不会_{又听说可以积分，懒得算} 遂采用非高等数学做法。

#include 
using namespace std;
const double pi = acos(-1.0);
double a1, b1, a2, b2;
double solve()
{
     
    double ans = 0.0;
    //第一象限交点坐标
    double x = sqrt((b1 * b1 - b2 * b2) * a1 * a1 * a2 * a2 / (b1 * b1 * a2 * a2 - b2 * b2 * a1 * a1));
    double y = sqrt((a1 * a1 - a2 * a2) * b1 * b1 * b2 * b2 / (a1 * a1 * b2 * b2 - b1 * b1 * a2 * a2));
    //计算相交部分的面积
    double theta1 = asin(y / b1), theta2 = asin(y / b2);
    ans = a1 * b1 * ((pi - 2 * theta1) + sin(2 * theta1)) + a2 * b2 * (2 * theta2 + sin(2 * theta2)) - 4 * x * y;
    return ans;
}
int main(){
     
    int n;
    scanf("%d", &n);
    while (n--){
     
        scanf("%lf%lf%lf%lf", &a1, &b1, &a2, &b2); 
        if(a1 <= a2) printf("%.1lf\n", pi * a2 * b2);
        else if(b1 >= b2) printf("%.1lf\n", pi * a1 * b1);
        else printf("%.1lf\n", pi * (a1 * b1 + a2 * b2) - solve()); 
    }
    return 0;
}

M.输入输出

这题考视力。

$m$个区间不重合，那直接区间长度求和即可，$k$个数据连读都不用读。

#include 
using namespace std;

int main(){
     
    int n, m, k, ans; cin >> n >> m >> k;
    for(int i = 0; i < m; i++){
     
        int x, y; cin >> x >> y;
        ans += (y - x);
    }
    cout << ans << endl;
    return 0;
}