滑动窗口算法总结及相关例题
文章目录
-
- 1. 算法思想
-
- 1.1 思想
- 1.2 套路代码
- 1.3例题精讲
-
- 1.3.1 最小覆盖子串
- 1.3.2 找到字符串中所有字母异位词
- 2. 相关例题
-
- 2.1. 重复的DNA序列
- 2.2. 存在重复元素 II
这里标注一下,本文参考于 《labuladong的算法小抄》
1. 算法思想
1.1 思想
滑动窗口,顾名思义:
滑动的窗口,其实就是使用双指针进行维护一个窗口。经过相关题目的练习,可以得出该窗口大小有固定大小的例题,也有不固定大小的例题。我们要根据相应的题目进行分析。而如果窗口是固定大小的,我们一般会根据窗口大小要超越固定大小而进行缩小窗口。而不是固定大小的窗口的就根据题目具体意思进行相应的窗口缩小。
1.2 套路代码
int l = 0, r = 0;
while(r < s.length()){
扩大窗口
c是要添加进去的字符
char c = s.charAt(r);
r ++;
这里进行相关的操作
while(窗口需要缩小时){
缩小窗口
d是要从窗口中出去的字符
char d = s.charAt(l);
l ++;
这里进行相关的操作
}
}
相关模板讲解:
- 在这里我们使用的是双指针算法技巧,初始化
l = 0 ,r = 0 - 我们这里维护的区间窗口为
[l,r)。 r作为右指针进行扩大窗口,c是放入窗口内部的字符l作为左指针进行缩小窗口,d是从窗口中去除的字符- 那么
其他需要加进来的代码就是题目要求我们维护的相应的数据结构,和维护该数据结构的相关操作了。看我博客的友友们要随机应变哦。
1.3例题精讲
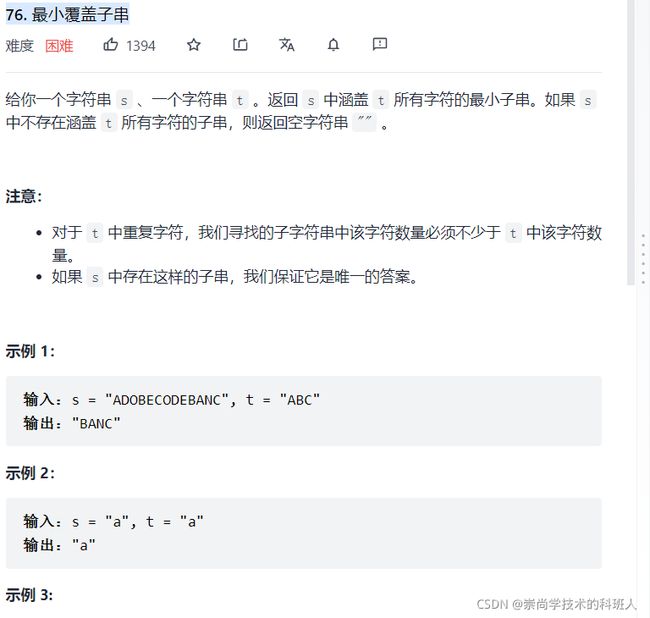
1.3.1 最小覆盖子串
- 在扩大窗口的同时,我们需要维护什么?
因为题目要我们求的是包含相应模板串中的所有字符,那么相应的字符可能是分散于我们求出来的答案中的,所以我们需要去维护
一个名为need的map集合存下模板串的所有字符及个数。还要一个名为win的map集合存下相应主串中滑动窗口中是上一个map集合中所包含的字符,还需要一个变量valid存下滑动窗口中和模板串中对应字符的个数相同的字符个数,因为是要求子串,所以还需要一个start记录相应的起始下标,len记录相应的长度。
- 什么时候缩小窗口?
当
valid等于need的大小时,就是相应的主串的滑动窗口包含模板串的所有字符了,此时需要缩小窗口。
3.在什么地方、什么时候更新start和len?
在
内层while中进行更新。当len小于r - l时。
AC代码:
public String minWindow(String s, String t) {
Map<Character,Integer> map = new HashMap<>();
Map<Character,Integer> map2 = new HashMap<>();
for(int i = 0; i < t.length(); i ++) map.put(t.charAt(i),map.getOrDefault(t.charAt(i),0) + 1);
int l = 0, r = 0;
int valid = 0;
int start = 0, len = Integer.MAX_VALUE;
while(r < s.length()){
char c = s.charAt(r);
r ++;
if(map.containsKey(c)){
map2.put(c,map2.getOrDefault(c,0) + 1);
if(map.get(c).equals(map2.get(c))){
valid ++;
}
}
while(valid == map.size()){
if(r - l < len){
start = l;
len = r - l;
}
char d = s.charAt(l);
l ++;
if(map.containsKey(d)){
if(map.get(d).equals(map2.get(d))){
valid --;
}
map2.put(d,map2.get(d) - 1);
}
}
}
return len == Integer.MAX_VALUE ? "" : s.substring(start,start + len);
}
特别提醒:
Byte,Short,Integer,Long 这 4 种包装类默认创建了数值 [-128,127] 的相应类型的缓存数据,Character 创建了数值在 [0,127] 范围的缓存数据,Boolean 直接返回 True Or False。 两种浮点数类型的包装类 Float,Double 并没有实现常量池技术。
所以如果是超出相应的范围,就不能使用
==判断数值大小,而必须使用equals方法
1.3.2 找到字符串中所有字母异位词
- 题目分析
这是
窗口大小固定的相关例题。上面那一道是窗口大小不是固定的。
- 所需要维护的数据结构?
因为模板串的字符顺序和主串的不一定相同,所以
维护的数据结构和上面的一样。这里不再过多讲解。
- 什么时候缩小窗口?
因为是固定大小的窗口,所以一般是
窗口大小等于相应的窗口大小时。先进行 是否符合要求判断,然后进行缩小窗口。
AC代码:
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> findAnagrams(String s, String p) {
Map<Character,Integer> need = new HashMap<>();
Map<Character,Integer> win = new HashMap<>();
// 初始化need
for(int i = 0; i < p.length(); i ++) need.put(p.charAt(i),need.getOrDefault(p.charAt(i),0) + 1);
int l = 0, r = 0;
int valid = 0;
while(r < s.length()){
char c = s.charAt(r);
r ++;
if(need.containsKey(c)){
win.put(c,win.getOrDefault(c,0) + 1);
if(need.get(c).equals(win.get(c))){
valid ++;
}
}
while(r - l >= p.length()){
// 相应的操作
if(valid == need.size()) list.add(l);
char d = s.charAt(l);
l ++;
if(need.containsKey(d)){
if(need.get(d).equals(win.get(d))){
valid --;
}
win.put(d,win.get(d) - 1);
}
}
}
return list;
}
}
可以练手的相关题目:
567. 字符串的排列
这里对前面的滑动窗口问题进行总结:
前面的三个问题是难度比较高的三个滑动窗口问题,因为
他们的对应的模板串的字符在主串中相应位置不是固定的,所以我们使用valid进行描述到达相应的标准,但是我们需要对我们所确定的区间进行字符记录,且记录的字符要是相应的模板串中含有的。
2. 相关例题
后面的问题就相对比较简单:
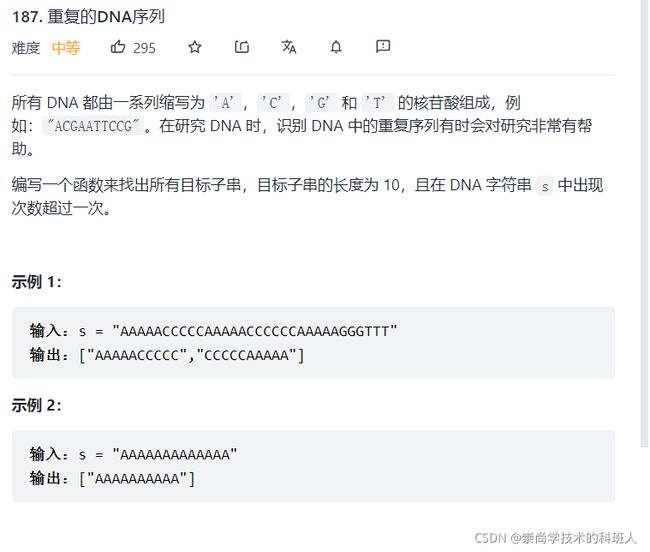
2.1. 重复的DNA序列
- 题目分析
其实
定长是10,而又是相应的字符串,并且不和前面相应的例题一样,他这相应的字符顺序截取的是什么就是什么,不需要改变。那么就可以直接根据相应的substirng。但是就是需要统计出现的次数。
- 维护的数据结构
map集合。截取后存入相应的map集合,边放边存。然后根据条件进行判断。
AC代码:
class Solution {
public List<String> findRepeatedDnaSequences(String s) {
int L = 10;
List<String> list = new ArrayList<>();
Map<String,Integer> map = new HashMap<>();
for(int i = 0; i <= s.length() - L; i ++){
String a = s.substring(i,i + L);
map.put(a,map.getOrDefault(a,0) + 1);
if(map.get(a) == 2){
// 为什么是== 2的时候,如果是大于2的话就会导致冗余情况
list.add(a);
}
}
return list;
}
}
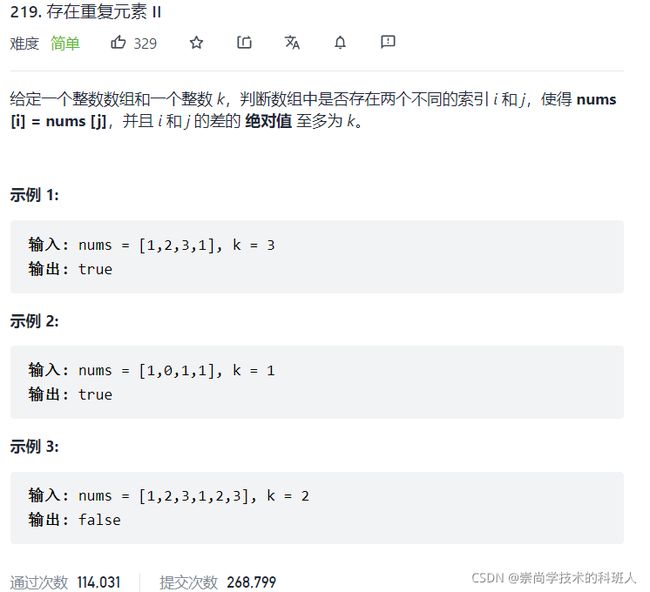
2.2. 存在重复元素 II
- 题目分析
这是
窗口大小固定的相关例题。上面那一道是窗口大小不是固定的。
- 维护的数据结构?
set集合,因为需要判断在前面的区间中是否出现过,所以使用set集合
- 缩小窗口的时机
因为这里维护的是
[i - k + 1,i]区间,所以当set.size() > k的时候缩小窗口。
AC代码:
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> set = new HashSet<>();
for(int i = 0; i < nums.length; i ++){
// 相当于一个数字在前面的一段区间内只能出现一次
// 每次遍历的时候加入set集合
// 该步骤简化了判断在区间距离小于k + 1的情况下是否存在相同元素
if(set.contains(nums[i])) return true;
// 在这里进行添加的原因是前面已经判断过了,set集合中不存在相应的重复元素
set.add(nums[i]);
if(set.size() > k){
// 但是set集合中的元素个数不能超过k + 1个
set.remove(nums[i - k]);
}
}
return false;
}
}
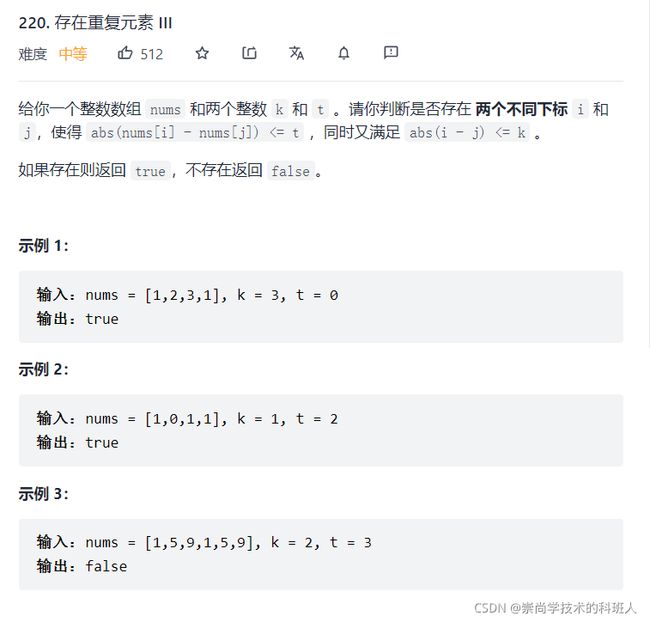
- 题目分析
这里的思路和前面的相似。
- 注意点
但是就是我们这里需要说明的是
添加操作的相应的位置改变。因为前面的那一道题是判断过集合不存在相应的元素,才进行添加。而我们这里没有。
if(ts.size() + 1 > k){
ts.remove(nums[i - k] * 1L);
}
ts.add(nums[i] * 1L);
AC代码:
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
if(k == 0) return false;
TreeSet<Long> ts = new TreeSet<>();
for(int i = 0; i < nums.length; i ++){
Long u = nums[i] * 1L;
// TreeSet 是一个可以提供找到大于相应值的最小值 和 一个可以找到小于相应值的最大值的方法
Long f = ts.floor(u);
Long r = ts.ceiling(u);
if(f != null && u - f <= t) return true;
if(r != null && r - u <= t) return true;
if(ts.size() + 1 > k){
ts.remove(nums[i - k] * 1L);
}
ts.add(nums[i] * 1L);
}
return false;
}
}
学到的新知识:
TreeSet: 一个可以提供大于相应元素的最小值和一个可以提供小于相应元素最大值的集合。