T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction 用于交通流预测的时序GCN
T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction
Abstract
准确、实时的交通预测是智能交通系统的重要组成部分,对城市交通规划、交通管理和交通控制具有重要意义。然而,由于受城市路网拓扑结构和动态随时间变化规律的制约,交通预测一直被认为是一个开放的科学问题。为了同时捕获网络的时空相关性,本文提出了一种基于神经网络的交通预测方法——时间图卷积网络(T-GCN)模型,该模型与图卷积网络(GCN)和门控递归单元(GRU)相结合。其中,GCN用于学习复杂拓扑结构,捕获空间相关性;门控递归单元(GRU)用于学习交通数据的动态变化,捕获时间相关性。然后,采用T-GCN模型进行基于城市道路网络的交通预测。实验表明,T-GCN模型能够从交通数据中获得时空相关性,其预测效果优于现实交通数据集的最新基线。
T-GCN tensorflow实现可以通过https://github.com/lehaifeng/T-GCN获得。
Introduction
从介绍可以看出,这篇文章和我们的一篇论文在方法论上很相似,我们解决的是从多特征角度出发预测区域级通讯强度的问题,而本文解决的是基于时空特征的区域交通流量问题;在论文撰写上也有很多相似的结构,这里直接摘要原文进行重点内容说明:
- 问题重要性阐述:
WITH the development of Intelligent Traffic Systems, traffic forecasting has received more and more attention. It is a key part of an advanced traffic management system and is an important part of realizing traffic planning, traffic management, and traffic control.
- 预测问题意义阐述:
Traffic forecasting can provide not only a scientific basis for traffic managers to sense traffic congestion and limit vehicles in advance but also security for urban travelers to choose appropriate travel routes and improve travel efficiency [1]-[3].
- 时空依赖性的挑战:
**Spatial dependence: **
城市路网的拓扑结构决定着交通量的变化。上游道路交通状况通过传递效应影响下游道路交通状况,下游道路交通状况通过反馈效应[4]影响上游道路交通状况。
Temporal dependence
相关工作简析:
时间要素提取模型:
Autoregressive Integrated Moving Average (ARIMA) model [5], [6], the Kalman filtering model [7], the support vector regression machine model [8], [9], the k-nearest neighbor model [10], the Bayesian model [11], and partial neural network model [12], [13].
缺点:
上述方法考虑了交通状况的动态变化而忽略了空间依赖性,使得交通状况的变化不受路网的限制,无法准确预测交通数据的状态。
空间要素提取模型:
To characterize the spatial features better, some studies [14]–[16] introduce a convolution neural network for spatial modeling;
缺点:
而卷积神经网络通常用于欧氏数据[17],如图像、规则网格等。这种模型无法在具有复杂拓扑结构的城市道路网络环境下工作,因此在本质上无法描述空间依赖性。
三点贡献:
- T-GCN模型集成了图卷积网络和门控递归单元,可分别捕获空间和时间特征。
- T-GCN模型在不同预测层次下的预测结果是稳定的,说明T-GCN模型不仅可以实现短期预测,还可以用于长期交通预测任务。
- 在两个真实数据集上的实验证明本方法比所有基准方法的预测误差降低了约1.5%-57.8%
Related Work
这里的相关工作从模型的角度进行划分,按照时间的顺序来说明:
Model-driven approach
- 基于先验知识,类似专家系统的方法:解释交通量、速度和密度之间的瞬时和稳态关系。
- 表示方法(representative medthods): 这些模型的构建需要强大的计算能力[22],并且容易受到交通干扰和采样点间距等的约束。
Data-driven approach
参数化模型以回归函数为前提,通过对原始数据的处理确定参数,进而实现基于回归函数的交通预测。
- time series model 时序模型 时间序列模型将观察到的时间序列拟合到参数模型中以预测未来数据。
- linear regression model 线性回归模型 线性回归模型根据历史交通数据建立回归函数来预测交通流量。
时间序列和回归分析的核心区别在于对数据的假设:回归分析假设每个样本数据点都是独立的;而时间序列则是利用数据之间的相关性进行预测。
传统的参数化模型算法简单,计算方便。然而,这些模型依赖于平稳假设,不能反映交通数据的非线性和不确定性特征,不能克服交通事故等随机事件的干扰。
However, these models depend on the assumption of stationary, cannot reflect the nonlinearity and uncertainty characteristics of traffic data, and cannot overcome the interference of random events such as traffic accidents.
常见的非线性模型包括the k-nearest neighbor model [10], the support vector regression model [8], [9], [35], the Fuzzy Logic model [36], the Bayesian network model [11], the neural network model.
[8]C. H. Wu, J. M. Ho, and D. T. Lee, “Travel-time prediction with support vector regression,” IEEE Transactions on Intelligent Transportation Systems
[9]Z. S. Yao, C. F. Shao, and Y. L. Gao, “Research on methods of short termtraffic forecasting based on support vector regression,” Journal of Beijing Jiaotong University
[35]A. J. Smola and B. Schlkopf, “A tutorial on support vector regression,” Statistics and Computing
[36]H. Yin, S. C. Wong, J. Xu, and C. K. Wong, “Urban traffic flow prediction using a fuzzy-neural approach
根据空间(spatial dependece 是否被考虑),可以将深度学习模型分为两类:
- 仅考虑时间依赖的模型:
Park et al. [40] used Feed Forward NN to implement traffic flow prediction tasks. Huang et al. [12] proposed a network architecture consisting of a deep belief network (DBN) and a regression model and verified that the network can capture random features from traffic data on multiple datasets and this model improved prediction accuracy in traffic forecasting. In addition, since the recurrent neural network (RNN) and its variants have long short-term memory (LSTM) and the gated recurrent unit (GRU) can effectively use the self-circulation mechanism, they can learn temporal dependence well and achieve better prediction results[13], [41]
- 结合时空特征的方法:(基于CNN,使用欧式数据)
SAE model、 ST-ResNet、 CNN+LSTM、 ITRCN(CNN+GRU)、 FCL-Net、 DCNN+LSTM(SRCN)
基于图神经网络的工作的兴起:
Li等人[46]提出了一种DCRNN模型,该模型通过对图的随机游走捕获空间特征,通过编解码器结构捕获时间特征。
[46]Y. Li, R. Yu, C. Shahabi, and Y. Liu, “Graph convolutional recurrent neural network: Data-driven traffic forecasting
METHODOLOGY
问题定义
与常见的时序网络预测任务类似,不再赘述。
![]()
G为urban road构建的网络,其中节点为roads,X为路网中节点的属性特征(traffic speed, traffic flow, and traffic density)
学习他的写法:(关于CNN与GNN之间的应用区别)
Acquiring the complex spatial dependence is a key problem in traffic forecasting. The traditional convolutional neural
network (CNN) can obtain local spatial features, but it can only be used in Euclidean space, such as images, a regular
grid, etc. An urban road network is in the form of graph rather than two-dimensional grid, which means the CNN
model cannot reflect the complex topological structure of the urban road network and thus cannot accurately capture
spatial dependence.
学习他的写法:(GRU的变量描述)
见论文
损失函数:

L R E G L_{REG} LREG为L2正则项,以防止过拟合。
Experiment
几种扩充实验的方法:
1、增加baseline
2、增加评价指标
3、预测的时段长度分开讨论
4、模型隐藏层规模分开讨论
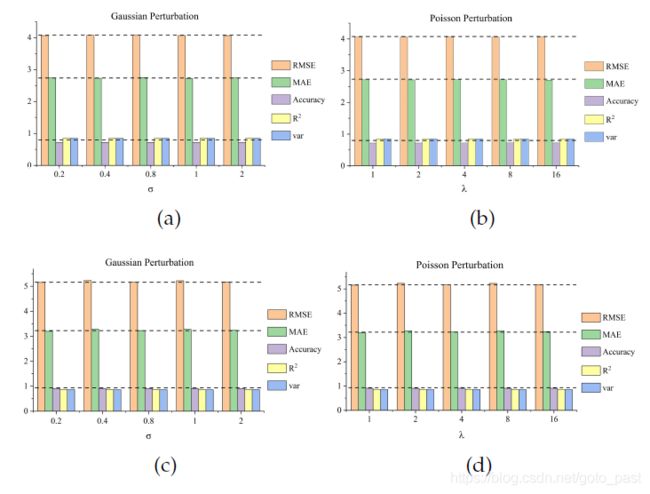
5、Perturbation Analysis and Robustness(扰动与鲁棒性分析)
在现实生活中,数据采集过程中不可避免地会产生噪声。为了测试TGCN模型的抗噪性,我们通过摄动分析实验测试模型的鲁棒性。