GCN在交通流预测方面的相关文章
文章目录
- GCN在交通流预测方面的相关文章
-
- (2018AAAI)Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting(STGCN)
- (2018ICLR)DIFFUSION CONVOLUTIONAL RECURRENT NEURAL NETWORK: DATA-DRIVEN TRAFFIC FORECASTING
- (2019IJCAI)STG2Seq: Spatial-Temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting
- (2019CIKM)Matrix Factorization for Spatio-Temporal Neural Networks with Applications to Urban Flow Prediction
- (2019IJ)Graph WaveNet for Deep Spatial-Temporal Graph Modeling
- (2020AAAI)Spatial-Temporal Synchronous Graph Convolutional Networks:A New Framework for Spatial-Temporal Network Data Forecasting(STSGCN)
- (2020AAAI)GMAN: A Graph Multi-Attention Network for Traffic Prediction
- (2020IJCAI)LSGCN: Long Short-Term Traffic Prediction with Graph Convolutional Networks
- (2020WWW)Traffic Flow Prediction via Spatial Temporal Graph Neural Network
- (2020NIPS)Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting
- (2020CIKM)Spatiotemporal Adaptive Gated Graph Convolution Networkfor Urban Traffic Flow Forecasting
GCN在交通流预测方面的相关文章
(2018AAAI)Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting(STGCN)
解决的问题
- 使用传统CNN将交通流考虑为网格结构(如图片,视频),而不是一般的域(如图)这样虽然能够学习到局部特征,但是不一定符合现实情况
- 使用RNN对时序进行建模,训练难度和参数量都很大
方法和创新:
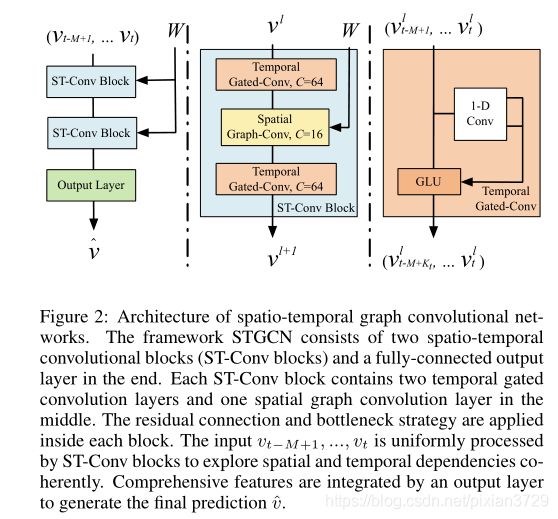
v l + 1 = Γ 1 l ∗ T ReLU ( Θ l ∗ G ( Γ 0 l ∗ T v l ) ) v^{l+1}=\Gamma_{1}^{l} * \mathcal{T} \operatorname{ReLU}\left(\Theta^{l} *_{\mathcal{G}}\left(\Gamma_{0}^{l} *_{\mathcal{T}} v^{l}\right)\right) vl+1=Γ1l∗TReLU(Θl∗G(Γ0l∗Tvl))
Critical Thinking:
- 使用卷积来代替LSTM类似的模式确实可以加快训练速度,但是是否也会导致缺失历史性数据信息,只能实现短期预测,无法实现长期预测
- 图卷积捕捉不同节点之间的信息来建模空间模型,似乎不能很好地利用不同区域之间的潜在关系
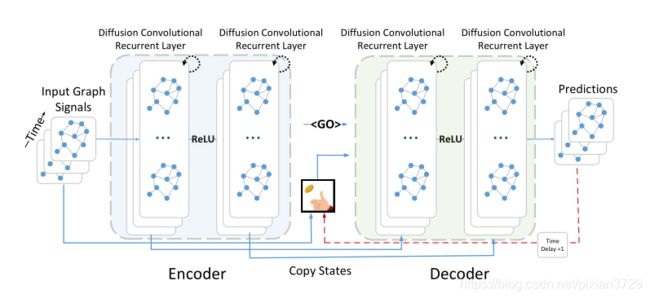
(2018ICLR)DIFFUSION CONVOLUTIONAL RECURRENT NEURAL NETWORK: DATA-DRIVEN TRAFFIC FORECASTING
解决的问题:
- 之间的交通问题都是在欧式空间进行计算,但是没有考虑到非欧空间的建模
- 由于空间复杂性和时间多边形,交通预测比较困难
方法和创新:
(2019IJCAI)STG2Seq: Spatial-Temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting
解决的问题:
- 基于CNN的方法将区域划分为网格进行,只能对近区或者远区之间的欧式关系进行建模,但是不能对非欧式距离进行建模
- 基于RNN的架构需要多次迭代,对长时间依赖进行建模会导致信息遗忘
- 不同时间步之间可能存在不同的影响
方法:使用分层图卷积来捕获时空相关性,多个分层卷积进行叠加后使用门控进行输出控制,对历史乘客数据进行长期编码,对单步预测数据进行短期编码,使用注意力进行输出
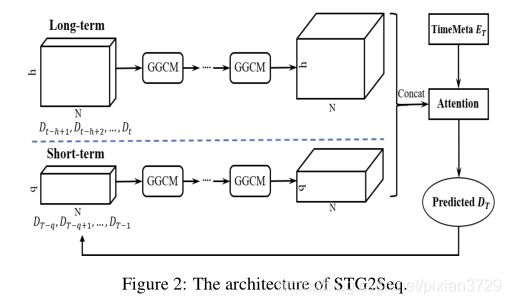

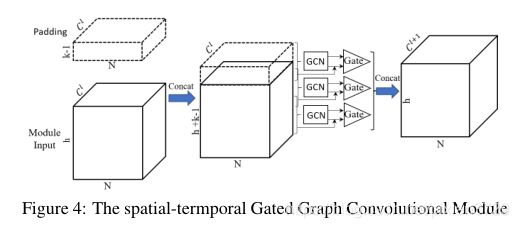
Critical Thinking:
- 所用图结构是通过判断两个区域之间的需求量分布来判断是否有相关性,虽然能够捕捉到一些兴趣区域的相似性,但是是否合理值得讨论,能否事先定义图结构或者通过学习的方式来学习图结构
(2019CIKM)Matrix Factorization for Spatio-Temporal Neural Networks with Applications to Urban Flow Prediction
解决的问题:
- 不同的区域存在潜在功能性,会影响模型预测,如果模型使用共享参数无法做出准确预测,如何在考虑潜在区域功能下建立模型来协同预测城市流量
- 如何使得框架能够适用和简单
方法/创新:使用个特定区域预测器,
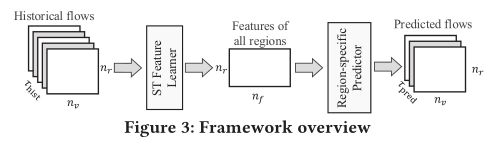
下图为特定区域预测器的结构,由非线性层和稠密矩阵分解层组成
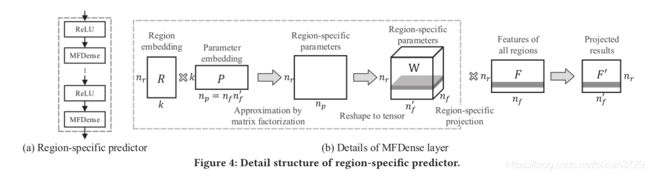
Y ^ = H ( m ) ( σ ( … H ( 1 ) ( σ ( F ) ) … ) ) \hat{\mathbf{Y}}=\mathcal{H}^{(m)}\left(\sigma\left(\ldots \mathcal{H}^{(1)}(\sigma(F)) \ldots\right)\right) Y^=H(m)(σ(…H(1)(σ(F))…))
其中 H ( m ) \mathcal{H}^{(m)} H(m)代表稠密矩阵分解层, F F F代表抽取出来的时空特征,作者想要为每个区域都特定一组参数,所以参数量为 W = [ W 1 , … , W n r ] ∈ R n r × n f ′ × n f , \mathrm{W}=\left[W_{1}, \ldots, W_{n_{r}}\right] \in\mathbb{R}^{n_{r} \times n_{f}^{\prime} \times n_{f}}, W=[W1,…,Wnr]∈Rnr×nf′×nf,where W i ∈ R n f ′ × n f W_{i} \in \mathbb{R}^{n_{f}^{\prime} \times n_{f}} Wi∈Rnf′×nf,将参数分解为区域embedding和参数embedding近似原始参数
(2019IJ)Graph WaveNet for Deep Spatial-Temporal Graph Modeling
解决的问题:
- 1)之前的研究假设图结构反应了节点间真正的依赖关系,但是当一个连接不需要两个节点间的关系,以及两个节点间的关系可以被忽略时;2)还有一种情况,存在一些节点虽然没有连接,但是却有相似的模式
- 基于RNN的模型存在迭代速度慢耗时的情况,基于一维卷积的CNN对于感受野的范围仅是线性增大,不能有效建模时间相关性
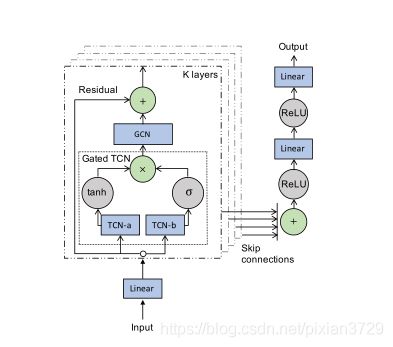
方法/创新:
Z = ∑ k = 0 K P f k X W k 1 + P b k X W k 2 + A ~ a p t k X W k 3 Z = \sum _ { k = 0 } ^ { K } P _ { f } ^ { k } X W _ { k 1 } + P _ { b } ^ { k } X W _ { k 2 } + \tilde { A } _ { a p t } ^ { k } X W _ { k 3 } Z=k=0∑KPfkXWk1+PbkXWk2+A~aptkXWk3
2. 时序卷积层
(2020AAAI)Spatial-Temporal Synchronous Graph Convolutional Networks:A New Framework for Spatial-Temporal Network Data Forecasting(STSGCN)
解决的问题:
- 当前的模型都是通过单独建立时空组件来分别捕获时间空间相关性,但是当前时刻同一个节点会在下一时刻影响自己也会影响下一时刻的邻居
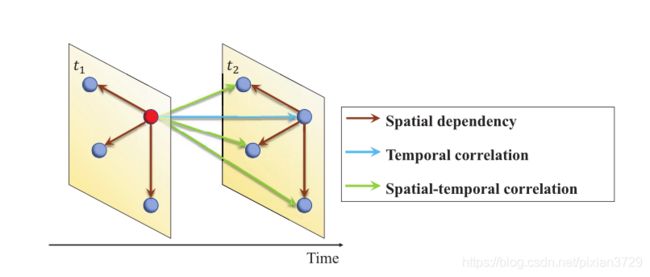
时空图中的每个节点都可以在同一时间步直接影响其相邻节点,并且这种影响是从实际的空间依赖性得出的。同时,由于时间序列中的时间相关性,每个节点也可以在下一时间步直接影响自己。此外,由于同步的时空相关性,每个节点都可以在下一时间步直接影响其邻居节点。 - 不同节点表现出时空异质性,即住宅区、商业区在不同时间段表现出不同的模式
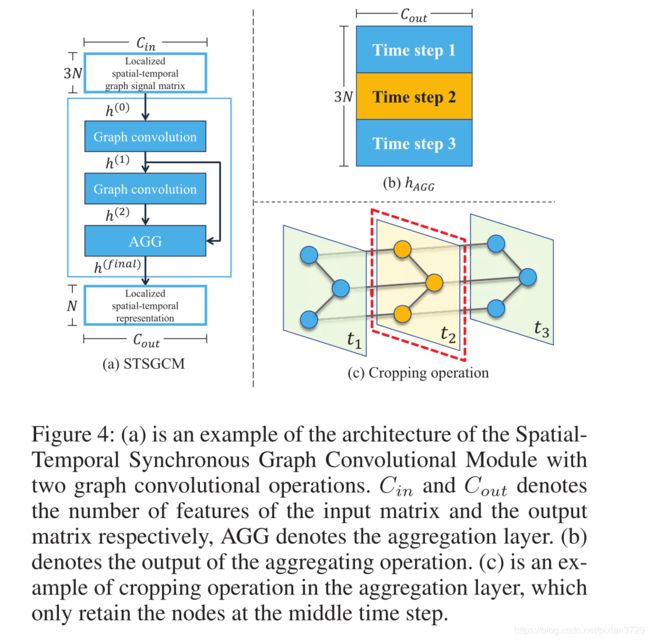
方法及创新:
- 构建了时空图卷积模块,直接可以同步地捕捉时空相关性
- 构造多模块层学习远程时空异质性,在每个时间段部署多个模块,从而能够每个模块专注于提取局部相关性
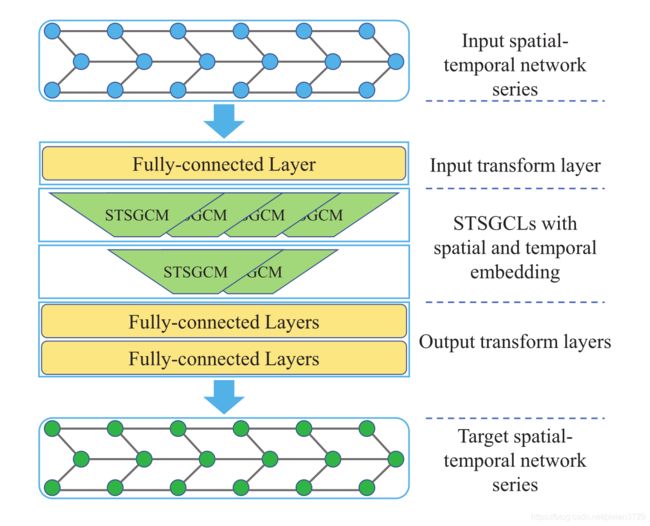
Figure 2: STSGCN architecture. Our STSGCN consists of multiple Spatial-Temporal Synchronous Graph Convolutional Layers (STSGCLs) with an input and an output layer. It uses an input layer to transform the input features into a higher dimensional space. Then stacked mulitple STSGCLs capture the localized spatial-temporal correlations and heterogeneities in spatial-temporal network series. Finally, it uses a multi-module output layer to map the final representations into the output space.
- 创新点:将时域空域进行连接,生成局部时空同步图来捕获节点间的时空关系和异质关系,
- 不同的局部时空图之间对于预测的权重没有考虑,因为不是每个局部时空图对于每个节点的预测权重都是相同的,通过直接concat是否错失了这种局部重要性关系,比如离预测时刻越近的局部时空对于决策的影响越大
(2020AAAI)GMAN: A Graph Multi-Attention Network for Traffic Prediction
解决的问题:看试验效果主要针对长期的交通流预测
- 时间和空间的复杂相关性,道路路网的不同节点间相互影响,各个节点对于自身的影响,以及动态的交通流之间的相互影响
- 对于长期预测问题,会有误差逐渐累积的过程
方法及创新:
- 使用时空注意机制分别对动态空间关系和非线性时间关系进行建模,同时使用门控机制来自适应融合时空注意力机制提取到的信息
- 使用转换注意力机制,将历史流量特征和未来时间直接进行建模,以减少误差传播
网络结构:
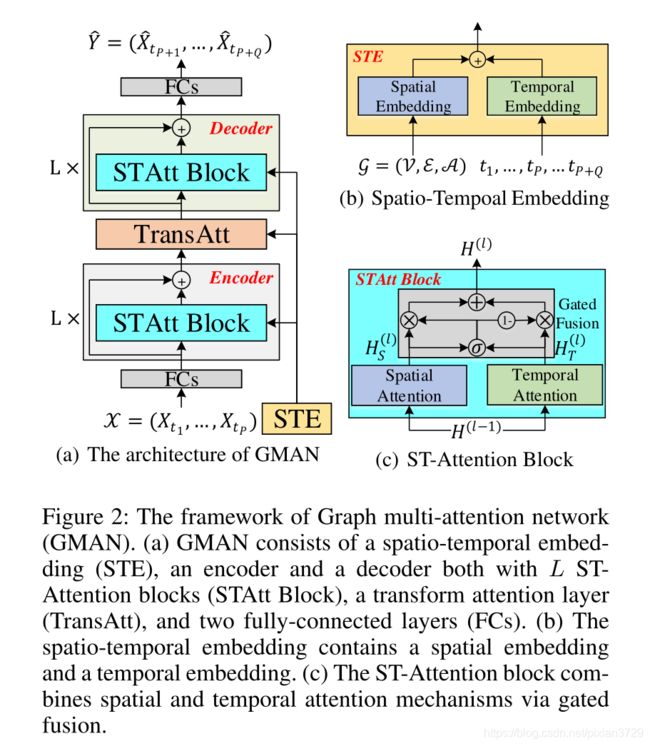
右上的spatial embedding通过node2vector得到,而temporal embedding由对一周,每个时刻的one-hot进行表示
时空注意力机制如下所示:
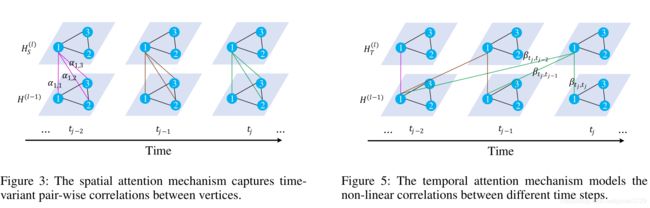
为了减少计算复杂度,通过分组注意力进行改进:
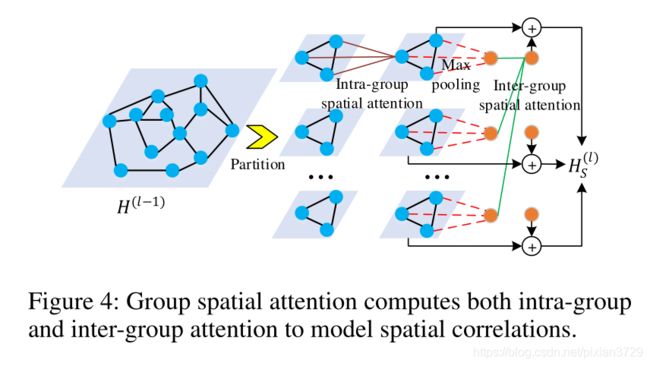
在编码器和解码器中间加入了转化注意力层,将历史数据和未来数据进行直接地注意力连接:
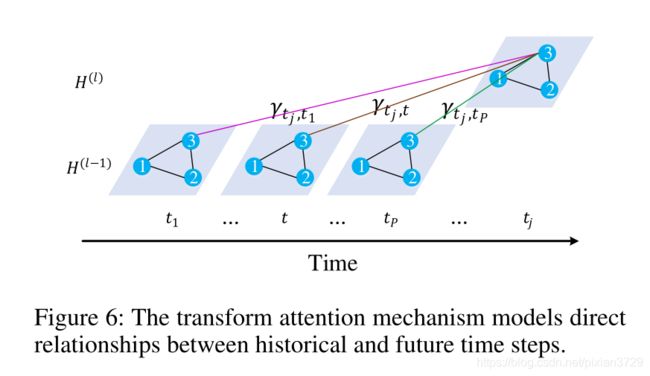
Critical Thinking:
- 和以往直接通过图卷积进行学习的方式不同,通过对整个网络进行表示学习,多处使用注意力机制来对时间空间的影响进行建模,通过分组注意力来减少计算复杂度,这样应该也是能够实现长期预测的关键因素。
- 如果对于小区域,每个节点都对相互影响是可以解释的,但是如果图很大的情况下,是否只有小区域内图节点相互影响,对于图卷积能否使用注意力机制来进行,比如不同节点和时间点对于邻居和自身的影响
(2020IJCAI)LSGCN: Long Short-Term Traffic Prediction with Graph Convolutional Networks
解决的问题:
- STGCN采用迭代机制,随着层次的加深,误差也不断增大,所以无法同时兼顾长短期交通预测,而ASTGCN和DCRNN采用非迭代机制,也无法同时兼顾长短期预测任务
- 迭代误差会随着时间逐渐增大
方法和创新:
针对长短期交通预测,提出LSGCN,采用空间门控块和门控线性单元卷积分别捕获时间和空间特征,同时提出了图注意网络cosAtt,将GCN和cosAtt集成到空间门控模块中
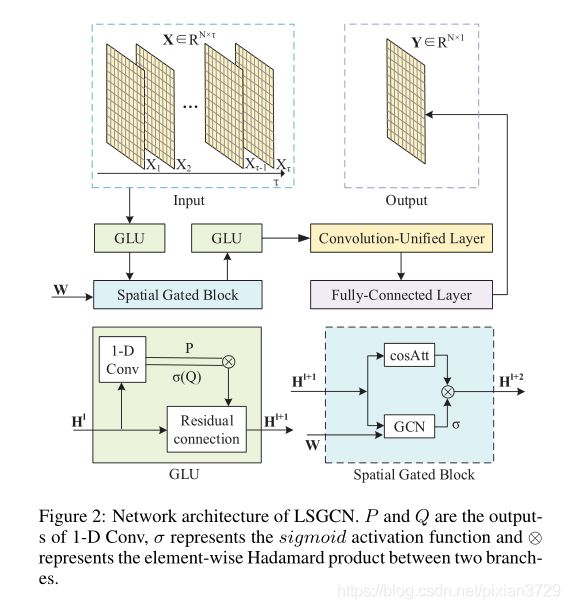
前半部分的GLU和STGCN是相同的,但是在对节点进行图卷积捕捉空间特征时,不是采用直接图卷积,同时还采用了一个图注意网络来捕获相似路况的情况,将GCN输出经过一个sigmod映射后决定输出cosAtt的哪些部分
关键公式如下,这里和GAT进行对比,可以看出GAT主要考虑的是邻居节点对于当前节点的影响,而cosAtt考虑的是全局注意力,下面是GAT和CosAtt的区别,
G A T e i j = A ( q i → w i , q j → w j ) , w i , w j ∈ F × F ′ a i j = softmax ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) q i ′ → = σ ( ∑ j ∈ N i a i j q j → w j ) ) GAT\\ e_{i j}=A\left(\overrightarrow{q_{i}} w_{i}, \overrightarrow{q_{j}} w_{j}\right), w_{i}, w_{j} \in F \times F^{\prime}\\ \begin{array}{c} a_{i j}=\operatorname{softmax}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)} \\ \left.\overrightarrow{q_{i}^{\prime}}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} a_{i j} \overrightarrow{q_{j}} w_{j}\right)\right) \end{array} GATeij=A(qiwi,qjwj),wi,wj∈F×F′aij=softmax(eij)=∑k∈Niexp(eik)exp(eij)qi′=σ(∑j∈Niaijqjwj))
c o s A t t e i j = cos ( h i , h j ) ⋅ w i j = h i × h j T ⋅ w i j ∥ h i ∥ × ∥ h j ∥ a i j = sigmoid ( e i j ) cos A t t i = ∑ j ∈ N ~ i a i j h j w i j cosAtt\\ \begin{array}{c} e_{i j}=\cos \left(h_{i}, h_{j}\right) \cdot w_{i j}=\frac{h_{i} \times h_{j}^{T} \cdot w_{i j}}{\left\|h_{i}\right\| \times\left\|h_{j}\right\|} \\ a_{i j}=\operatorname{sigmoid}\left(e_{i j}\right) \\ \cos A t t_{i}=\sum_{j \in \tilde{N}_{i}} a_{i j} h_{j} w_{i j} \end{array} cosAtteij=cos(hi,hj)⋅wij=∥hi∥×∥hj∥hi×hjT⋅wijaij=sigmoid(eij)cosAtti=∑j∈N~iaijhjwij
Critical Thinking:
- 这里主要考虑到了逐步预测导致的累计误差,作者提供的方法首先是简化网络结构,减少累计误差,使用了门控机制来捕获节点的空间关联
- 作者采用了全局注意机制,可以考虑到相似道路之间的关系从而捕获节点之间变化的相似性
(2020WWW)Traffic Flow Prediction via Spatial Temporal Graph Neural Network
解决的问题:
- 现有基于GNN和RNN的方法不能反应道路中的动态空间信息,简单的静态空间临近不能很好的建模
- RNN间接对时间依赖性建模,如果时间路径过长的话,很难学习到长期的依赖关系,全局时间信息也有重要影响
方法创新:
- 提出了一个新的图神经网络及位置注意机制,从而更好地从临近道路聚集交通信息
- 结合递归网络和转换网络来捕捉全局和局部特征
- 提出了新的STGNN建模复杂拓扑和时间相关性的数据
- 这里S-GNN与GCN不相同,作者认为空间空间节点间的联系是复杂的,不应该均匀聚集到给定中心节点,所以提出要学习一个每个节点的位置表示·
R [ i , j ] = exp ( ϕ ( Score ( p i , p j ) ) ) ∑ k = 1 N exp ( ϕ ( Score ( p i , p k ) ) ) \mathrm{R}[i, j]=\frac{\exp \left(\phi\left(\operatorname{Score}\left(\mathrm{p}_{i}, \mathrm{p}_{j}\right)\right)\right)}{\sum_{k=1}^{N} \exp \left(\phi\left(\operatorname{Score}\left(\mathrm{p}_{i}, \mathrm{p}_{k}\right)\right)\right)} R[i,j]=∑k=1Nexp(ϕ(Score(pi,pk)))exp(ϕ(Score(pi,pj)))
通过学习这种位置信息表示,构建了一个新的图,然后在新图上使用图卷积(思想是节点间的关系不仅仅是空间位置上的关系,需要网络自己去学习一个位置表示关系,很像让网络自己去学一个拓扑表示)
mask ( R ) = { R i j , if A ~ i j > 0 0 , otherwise X out = σ ( D ~ R − 1 / 2 R ~ D ~ R − 1 / 2 X i n W ( l ) ) \operatorname{mask}(\mathbf{R})=\left\{\begin{array}{ll} \mathbf{R}_{i j}, & \text { if } \tilde{\mathbf{A}}_{i j}>0 \\ 0, & \text { otherwise } \end{array}\right.\\ \mathrm{X}_{\text {out}}=\sigma\left(\tilde{\mathrm{D}}_{R}^{-1 / 2} \tilde{\mathrm{R}} \tilde{\mathrm{D}}_{R}^{-1 / 2} \mathrm{X}_{i n} \mathrm{W}^{(l)}\right) mask(R)={ Rij,0, if A~ij>0 otherwise Xout=σ(D~R−1/2R~D~R−1/2XinW(l))

这里就是使用transformer来捕获对每个节点的时间全局相关性
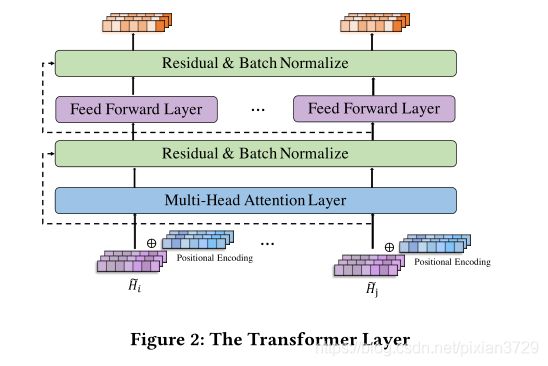
Q v i = H v i W Q , K v i = H v i W K , V = H v i W V Attention ( H v i ) = softmax ( ( H v i W Q ) ( H v i W K ) T d k H v i W V ) \mathrm{Q}^{v_{i}}=\mathrm{H}^{v_{i}} \mathrm{W}^{Q}, \mathrm{~K}^{v_{i}}=\mathrm{H}^{v_{i}} \mathrm{W}^{K}, \mathrm{V}=\mathrm{H}^{v_{i}} \mathrm{W}^{V}\\ \text { Attention }\left(\mathrm{H}^{v_{i}}\right)=\operatorname{softmax}\left(\frac{\left(\mathrm{H}^{v_{i}} \mathrm{W}^{Q}\right)\left(\mathrm{H}^{v_{i}} \mathrm{W}^{K}\right)^{T}}{\sqrt{d_{k}}} \mathrm{H}^{v_{i}} \mathrm{W}^{V}\right) Qvi=HviWQ, Kvi=HviWK,V=HviWV Attention (Hvi)=softmax(dk(HviWQ)(HviWK)THviWV)
(2020NIPS)Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting
解决的问题:
- 最近的方法都是在设计复杂的网络结构,在预定义的图中共享模式,预定义的图需要更多的专业知识且对图的结构敏感,以这种方式生成的图是直观的,但是不完整的,可能包含偏见
方法/创新:文章提出不适用预先定义的图结构使用共享的模式,而是学习每个节点特定的模式
- 节点自适应参数学习(NAPL)模块,学习每个流量序列的特定节点模式,分解传统GCN中的参数,根据节点嵌入从所有节点共享的权重池和偏差池生成特定节点参数
- 数据自适应图生成模块(DAGG),用于从数据中推断节点嵌入(属性),并在训练期间根据数据自适应生成图片生成图
具体实现(这里的思想值得学习):
-
节点自适应参数学习
常规的GCN可以表示为如下形式
Z = ( I N + D − 1 2 A D − 1 2 ) X Θ + b Z=\left(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) X \Theta+\mathbf{b} Z=(IN+D−21AD−21)XΘ+b
其中 A A A是邻接矩阵 ∈ R N × N \in R^{N×N} ∈RN×N, X 是 输 入 ∈ R N × C , θ 是 需 要 学 习 的 参 数 ∈ R C × F X是输入\in R^{N×C},\theta 是需要学习的参数 \in R^{C×F} X是输入∈RN×C,θ是需要学习的参数∈RC×F,这里从节点的角度来看相当于把从C维投影到F维(所有节点都共享参数 θ \theta θ),这里作者觉得虽然共享参数学到的是全部节点的最重要的特征,但是,由于交通问题的复杂性,不同的流量序列间存在不同的模式,所以建议为每个节点都学习一组参数,但是这里会出现另外一个问题,会导致参数 Θ ∈ R N × C × F \Theta \in R^{N×C×F} Θ∈RN×C×F,所以作者这里利用矩阵分解的思想,将参数分解为node-embedding E g ∈ R N × d E_g \in R^{N×d} Eg∈RN×d,以及权重池 W g ∈ R d × C × F W_g \in R^{d×C×F} Wg∈Rd×C×F,从解释上来说可以解释为节点i根据embedding从共享权重池中提取参数,所以图卷积可以表示为
Z = ( I N + D − 1 2 A D − 1 2 ) X E G W G + E G b G Z=\left(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) X E_{\mathcal{G}} W_{\mathcal{G}}+E_{\mathcal{G}} \mathrm{b}_{\mathcal{G}} Z=(IN+D−21AD−21)XEGWG+EGbG -
数据自适应图生成
这里作者不适用预先定于图结构,而是通过随机初始化的node embedding( E A E_A EA)来进行学习节点表示,直接代替归一化的拉普拉斯矩阵
D − 1 2 A D − 1 2 = softmax ( Re L U ( E A ⋅ E A T ) ) \boldsymbol{D}^{-\frac{1}{2}} A \boldsymbol{D}^{-\frac{1}{2}}=\operatorname{softmax}\left(\operatorname{Re} L U\left(\boldsymbol{E}_{\boldsymbol{A}} \cdot \boldsymbol{E}_{A}^{T}\right)\right) D−21AD−21=softmax(ReLU(EA⋅EAT))
所以GCN被改这个样子:
Z = ( I N + softmax ( Re L U ( E A ⋅ E A T ) ) ) X Θ \boldsymbol{Z}=\left(\boldsymbol{I}_{\boldsymbol{N}}+\operatorname{softmax}\left(\operatorname{Re} L U\left(\boldsymbol{E}_{\boldsymbol{A}} \cdot \boldsymbol{E}_{\boldsymbol{A}}^{T}\right)\right)\right) \boldsymbol{X} \Theta Z=(IN+softmax(ReLU(EA⋅EAT)))XΘ -
最后由上面两部分组成了自适应图卷积神经网络(AGCRN),具体就是将GRU中的多层感知机替换为节点自适应表示学习GCN,这里的节点embedding在各个AGCRN中
A ~ = softmax ( ReLU ( E E T ) ) z t = σ ( A ~ [ X : , t , h t − 1 ] E W z + E b z r t = σ ( A ∣ X : , t , h t − 1 ] E W r + E b r h ^ t = tanh ( A ~ [ X i , t , r ⊙ h t − 1 ] E W h ^ + E b h ^ h t = z ⊙ h t − 1 + ( 1 − z ) ⊙ h ^ t \begin{aligned} \widetilde{\boldsymbol{A}} &=\operatorname{softmax}\left(\operatorname{ReLU}\left(\boldsymbol{E} \boldsymbol{E}^{\boldsymbol{T}}\right)\right) \\ \boldsymbol{z}_{\boldsymbol{t}} &=\sigma\left(\widetilde{\boldsymbol{A}}\left[\boldsymbol{X}_{:, t}, \boldsymbol{h}_{\boldsymbol{t}-1}\right] \boldsymbol{E} \boldsymbol{W}_{\boldsymbol{z}}+\boldsymbol{E} \boldsymbol{b}_{\boldsymbol{z}}\right.\\ r_{t} &=\sigma\left(A \mid X_{:, t}, h_{t-1}\right] E W_{r}+E b_{r} \\ \hat{h}_{t} &=\tanh \left(\widetilde{A}\left[X_{i, t}, r \odot h_{t-1}\right] E W_{\hat{h}}+E b_{\hat{h}}\right.\\ h_{t} &=z \odot h_{t-1}+(1-z) \odot \hat{h}_{t} \end{aligned} A ztrth^tht=softmax(ReLU(EET))=σ(A [X:,t,ht−1]EWz+Ebz=σ(A∣X:,t,ht−1]EWr+Ebr=tanh(A [Xi,t,r⊙ht−1]EWh^+Ebh^=z⊙ht−1+(1−z)⊙h^t
这里网络的结构类似DCRNN,但是对GRU的改变又很像ConvLSTM的想法
Critical Thinking:
- 这里作者提出不要使用提前定义的邻接矩阵来进行图卷积,因为提前定义需要很多专业知识,通过节点自适应学习模块和数据自适应图生成模块来增强传统的图卷积网络,学习到了特定节点中不同的模式
- 但是从最后数据中可以看出,这样学习参数量还是比较大的,可能会导致内存溢出,特别当图的节点特别多的时候,作者的解决方法是图划分和子图训练(这里是否有可以改进的空间)
- 这里的适应性参数和图学习,相当于将预定义图转化为需要学习的embedding,然后通过矩阵分解来简化参数。
(2020CIKM)Spatiotemporal Adaptive Gated Graph Convolution Networkfor Urban Traffic Flow Forecasting
解决的问题:
- 之前的方法主要通过构建一个固定的图来建模空间依赖关系,但是道路之间的作用是相互的,是动态调整的
- 以前的方法使用GNN聚合邻居信息只考虑了局部临近性,但是没有考虑到全局上下文信息
方法/创新:
- 根据交通状况的空间相关性建模动态加权图,同时定义了道路节点的空间邻居和语义邻居分别表示道路的连通性和交通特征的上下文相似性
- 针对级联神经网络性能下降的问题,提出了一种自适应选通机制来选择性地更新和遗忘高维特征
定义了两个图:
一个空间相邻图,一个语义相邻图(及空间相连和使用DTW对齐后相邻,相当于多了一个捕获兴趣区域的图)
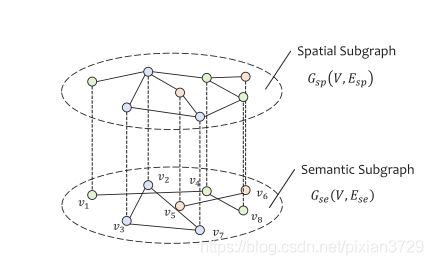
网络结构如下图:
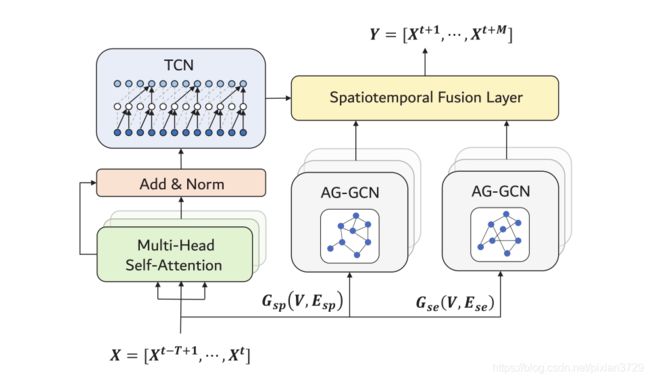
在时间维度上使用多头注意力自注意TCN提取每个节点的时间特征(相当于每个时间片分配一个权重)
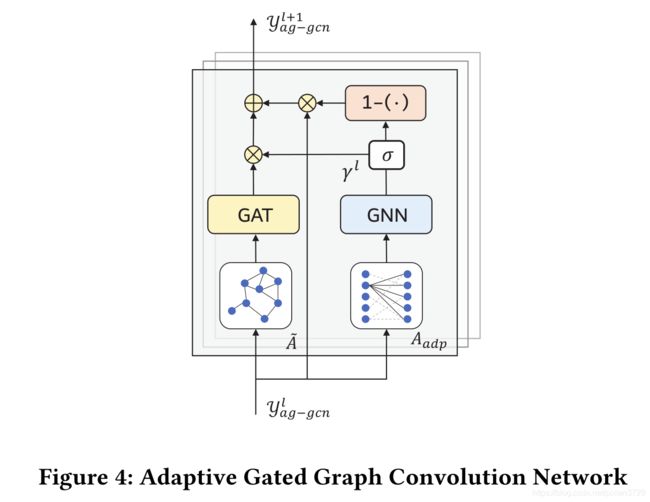
对于空间特征这里的图卷积分为两部分,左边是实际交通图(语义交通图),右边是自适应邻接矩阵,通过类似门控机制的图卷积通过自适应邻接矩阵来对图卷积后的结果进行门控,这里的图卷积使用了多头GAT,能够为聚合邻居信息时按照权重来聚合。
融合阶段
这里的融合方式有很多(文中直接采用直接concate),也可以使用maxpooling或者LSTM,为了避免多步预测造成的误差累积,这里直接采用一次预测多个时间步的方法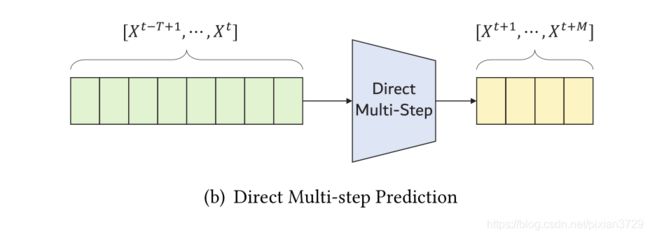
Critical Thinking:
- 提出的语义图按照DTW算法得到,这样得到的语义图是否能够真实反应节点间的信息(是否只需要自适应邻接矩阵就能够反应语义)
- 将TCN和GCN分开是否不能够很好利用空间和时间的特征