leetcode笔记总结——（8）三道题掌握 单调栈的使用(python和C++描述)

1、第一题：下一个更大元素I

1.1 题目描述：

1.2 方法一：暴力法

（1）思路：

题目中的关键信息：两个数组各自 没有重复元素。因此，可以对于每一个 nums1[i] 中的元素，先在 nums2 中找到它，然后向右遍历找到第 1 个大于 nums1[i] 的元素。

（2）python代码：

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        ret = []
        for num1 in nums1:
            index = nums2.index(num1) # 获取下标
            for i in range(index+1, len(nums2)):
                if nums2[i] > num1: # 找到了
                    ret.append(nums2[i])
                    break
            else: # 没找到
                ret.append(-1)
        return ret

（3）C++代码：

class Solution {
     
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
     
        vector<int> ret; //存放结果
        for(int i=0;i<nums1.size();++i)
        {
     
            bool found = false;
            vector<int>::iterator it = find(nums2.begin(), nums2.end(), nums1[i]); 
            int index = it - nums2.begin(); //寻找下标
            for(int j = index+1;j<nums2.size();++j)
            {
     
                if(nums2[j]>nums1[i])
                {
     
                    ret.push_back(nums2[j]);
                    found = true;
                    break;
                }
            }
            if(!found) ret.push_back(-1); //未找到
        }
        return ret;
    }
};

1.3 方法二：单调栈法

这道题使用暴力法很容易解决，但是这不是我们练习的目的，我们的目的是：通过这道题练习单调栈的使用。

因此，我们首先要知道单调栈是个什么玩意。栈（stack）是很简单的一种数据结构，先进后出的逻辑顺序，符合某些问题的特点，比如说函数调用栈。
单调栈实际上就是栈，只是利用了一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减）。
了解这个之后，我们接着看解题思路：

（1）思路：

根据题意，数组 nums1 视为询问。我们可以：
（1）先对 nums2 中的每一个元素，求出它的右边第一个更大的元素；
（2）将上一步的对应关系放入哈希表（HashMap）中；
（3）再遍历数组 nums1，根据哈希表找出答案。

因此，现在的关键在于怎么找出nums2中每一个元素，它的右边第一个更大的元素呢？（下面是力扣官方的解答）

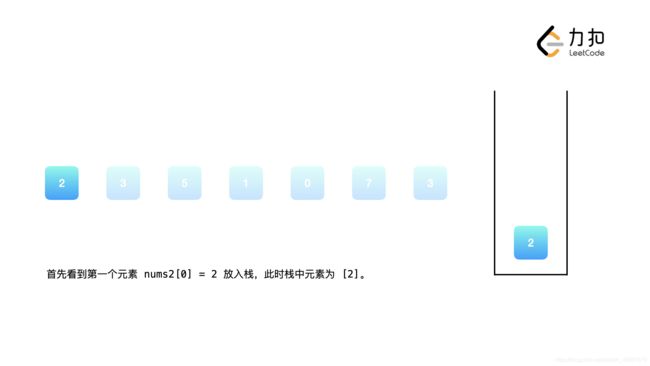
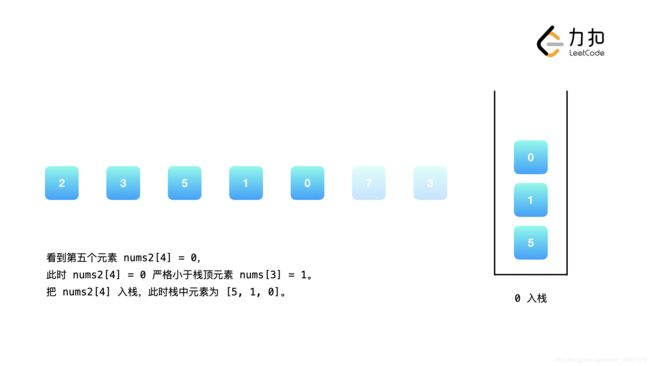
下面我们解释如何得到 nums2 的每个元素右边第 1 个比它大的元素，这里以 nums2 = [2, 3, 5, 1, 0, 7, 3] 为例进行说明，我们从左到右遍历数组 nums2 中的元素。









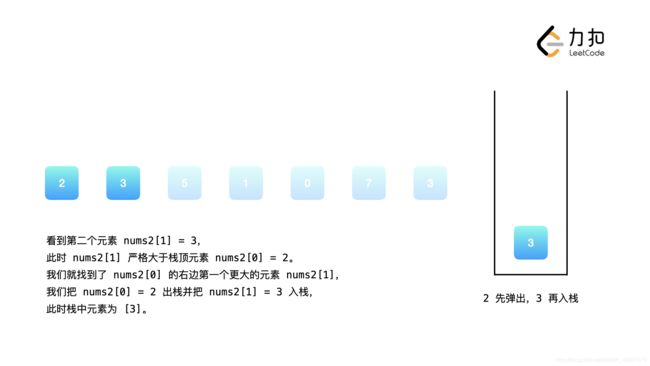
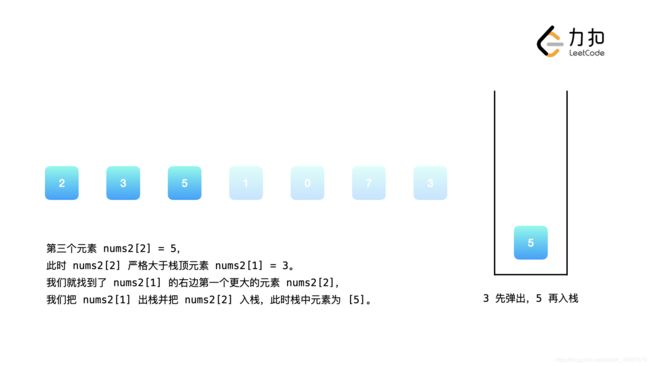
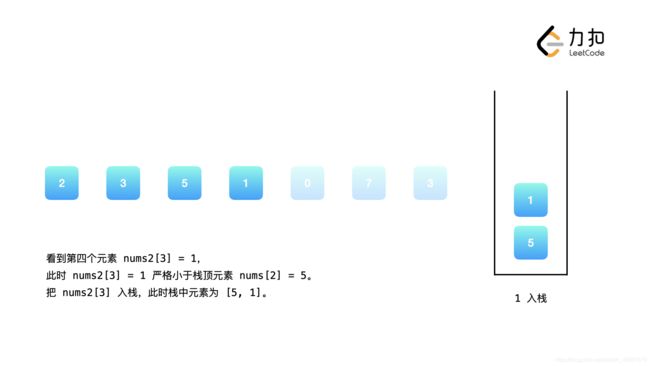
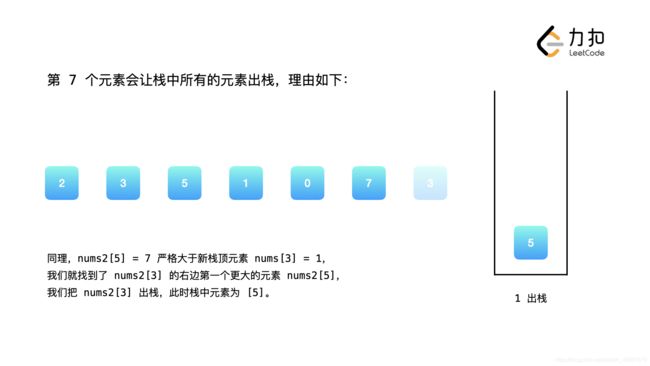
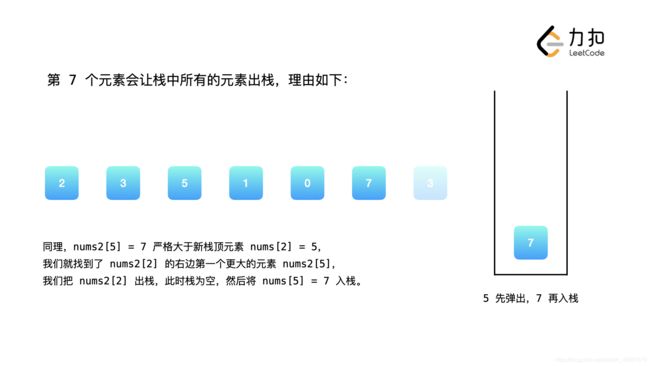
可以发现，我们维护的栈恰好保证了单调性：栈中的元素从栈顶到栈底是单调不降的。当我们遇到一个新的元素 nums2[i] 时，我们判断栈顶元素是否小于 nums2[i]，如果是，那么栈顶元素的下一个更大元素即为 nums2[i]，我们将栈顶元素出栈。重复这一操作，直到栈为空或者栈顶元素大于 nums2[i]。此时我们将 nums2[i] 入栈，保持栈的单调性，并对接下来的 nums2[i + 1], nums2[i + 2] ... 执行同样的操作。

这里我再解释一下：其实，就是让栈从大到小，因为我们要找下一个更大元素，那么遇到了比栈顶大的，不就说明当前栈顶的元素的下一个更大元素找到了么，同时，因为我们的栈，是从栈底到栈顶从大到小排列的，因此，要一直出栈到比当前这个对比的元素更大的元素才停止。这下明白了吧，还不明白，那就想想一下，人的身高：由于是单调的，因此，前面的这4个人的下一个更大元素，就是最后面的这个。

（2）python代码：

python代码因为在初始化字典（哈希表）的时候，能用字典生成式，所以直接赋值为-1了，因此最后就不用再遍历栈中的剩余元素了。

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        hash_table = {
     } # 存放nums2中找到的下一个最大值
        stack = []
        for i in range(len(nums2)):
            while stack and stack[-1] < nums2[i]:
                hash_table[stack.pop()] = nums2[i] # 出栈，并将当前元素作为栈顶的下一个更大值
            stack.append(nums2[i]) # 当前元素入栈
        res = [] # 结果列表
        for it in nums1: # 因为nums1是子集，所以遍历nums1找里面的下一个更大值
            res.append(hash_table.get(it, -1))
        return res

（3）C++代码：

class Solution {
     
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
     
        vector<int> res; //结果容器
        stack<int> s; //栈
        map<int, int> m; //哈希表
        
        // 先处理 nums2，把对应关系存入哈希表
        for(int i = 0;i<nums2.size();++i)
        {
     
            while(!s.empty() && s.top() < nums2[i])
            {
     
                auto temp = s.top(); //查看栈顶元素
                s.pop(); //出栈
                m[temp] = nums2[i]; //加入哈希表中
            }
            s.push(nums2[i]); //当前元素入栈
        }
        //因为此时栈中的元素肯定没有更大值看，因此将栈中的元素取出，并把对应的值设置为-1
        while(!s.empty())
        {
     
            m[s.top()] = -1;
            s.pop();
        }
        // // 遍历 nums1 得到结果集
        for(int i = 0;i<nums1.size();++i)
        {
     
            res.push_back(m[nums1[i]]);
        }
        return res;

    }
};

2、第二题：下一个更大元素II

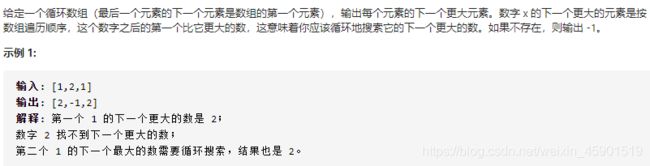
2.1 题目描述：

2.2 方法一：暴力法

（1）思路：

看完第一题，是不是觉得使用单调栈确实很巧妙，但是先别急，我们先使用暴力法解决这个问题，因为暴力法是我们先想到的方法。
思路：
因为要循环，所以我们把遍历过的数先放在一个数组中，这样的话，当我们当前的元素遍历完了一遍之后还是没找到下一个更大元素，那么就遍历数组中的元素，找到了则加入，没找到，则加入-1。

（2）python代码：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        ret = []
        queue = [] # 队列保存已经访问的元素
        for i in range(len(nums)):
            queue.append(nums[i])
            for j in range(i+1, len(nums)):
                if nums[j] > nums[i]:
                    ret.append(nums[j])
                    break
            else: # 没有大于的，那就遍历队列里的，也就是之前的元素
                for k in queue:
                    if k > nums[i]: # 之前的元素有大的，则加入
                        ret.append(k)
                        break
                else: # 之前的元素没有大的，则加入-1
                    ret.append(-1)
        return ret

（3）C++代码：

class Solution {
     
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
     
        vector<int> ret; //结果容器
        vector<int> save; // 存放访问过的元素,
        for(int i=0;i<nums.size();++i)
        {
     
            save.push_back(nums[i]); //将访问过的元素存入容器中
            bool found1 = false; //直接在数组的后面能找到的标志
            bool found2 = false; //找当前元素前面的元素是否有大的标志
            for(int j=i+1;j<nums.size();++j)
            {
     
                if(nums[i] < nums[j]) //找到了，则加入到ret中，并终止循环
                {
     
                    ret.push_back(nums[j]);
                    found1 = true;
                    break;
                }
            }if(!found1) //在后面没找到，找这个元素前面的
            {
     
                for(int k=0;k<save.size();++k)
                {
     
                    if(save[k] > nums[i])
                    {
     
                        ret.push_back(save[k]);
                        found2 = true;
                        break;
                    }
                }if(!found2){
      //没找到，则加入-1
                    ret.push_back(-1);
                }
            }
        }
        return ret;

    }
};

C++这个也太拉跨了，也可能是我的暴力法的代码不正确。

2.3 方法二：单调栈法

（1）思路：

我们可以使用单调栈解决本题。单调栈中保存的是下标，从栈底到栈顶的下标在数组nums 中对应的值是单调不升的。
每次我们移动到数组中的一个新的位置 i，我们就将当前单调栈中所有对应值小于nums[i] 的下标弹出单调栈，这些值的下一个更大元素即为nums[i]（证明很简单：如果有更靠前的更大元素，那么这些位置将被提前弹出栈）。随后我们将位置 i 入栈。
但是注意到只遍历一次序列是不够的，例如序列 [2,3,1]，最后单调栈中将剩余 [3,1]，其中元素 [1] 的下一个更大元素还是不知道的。
一个朴素的思想是，我们可以把这个循环数组「拉直」，即复制该序列的前 n−1 个元素拼接在原序列的后面。这样我们就可以将这个新序列当作普通序列，用上文的方法来处理。
而在本题中，我们不需要显性地将该循环数组「拉直」，而只需要在处理时对下标取模即可。

（2）python代码：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        stack = [] # 单调栈
        ret = [-1]*n # 初始化结果列表结果列表
        for i in range(n*2-1):
            while stack and nums[stack[-1]] < nums[i%n]: # 当栈不为空，并且栈顶元素小于当前访问元素
                ret[stack.pop()] = nums[i%n] # 将当前元素设置为栈顶元素的更大值
            stack.append(i%n) # 当前元素入栈
        return ret

（3）C++代码：

class Solution {
     
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
     
        int n = nums.size(); //长度
        vector<int>ret(n, -1); //结果容器初始化为-1
        stack<int> s; //单调栈
        for(int i=0;i<n*2-1;++i)
        {
     
            while(!s.empty() && nums[s.top()]<nums[i%n])//取余就相当于访问了两遍了
            {
     
                ret[s.top()] = nums[i%n]; //栈顶元素的下一个更大值为nums[i]
                s.pop(); //出栈
            }
            s.push(i%n); //将当前元素的下标入栈
        }
        return ret;
    }
};

2.4 总结：

做完了这两道题，我们会发现，其实1、2题都是：求一个数组中每个元素的下一个更大元素。
只不过第一题是：另外找了个子数组，因此我们在保存的时候使用了hash表来保存键值对，其目的是能在这个子数组中找到每一个对应的答案。
第二道题：就更简单了，其中要注意的是：为了保存方便保存在ret，单调栈中要保存对应的下标，如果不保存下标，那么在保存的时候就要找保存元素对应的下标。还有最重要的一个考点是：这个循环数组怎么访问？其实就是访问两遍，一个朴素的思想是，我们可以把这个循环数组「拉直」，即复制该序列的前 n−1 个元素拼接在原序列的后面。这样我们就可以将这个新序列当作普通序列，用上文的方法来处理。
而在本题中，我们不需要显性地将该循环数组「拉直」，而只需要在处理时对下标取模即可。

3、第三题：每日温度

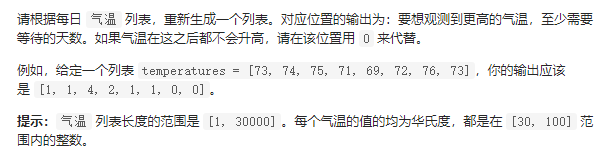
3.1 题目描述：

3.2 方法一：单调栈法

（1）思路：

看完这个题，这个不就是：求一个数组中每个元素的下一个更大值的变体么，区别在于存放的是每个元素到下一个更大元素的距离。
因此，我们还是使用前面的单调栈方法：
1、每个元素都进栈出栈一次，在进栈的时候，首先检查进栈的这个元素是不是比栈顶元素小，要是小，则直接入栈，要是大，那么一直出栈到栈顶元素不大于进栈的这个元素；
2、由于要求：每个元素到下一个更大元素的距离，那么我们在栈中保存每个元素的下标即可；
3、当每次找到下一个更大元素的时候，就使用下一个更大元素的下标 减 栈顶元素，得到的就是距离。
4、 在循环结束后，栈中有可能还剩部分元素。 但是这部分元素其实是递减的，也就是说后面没有哪天温度更高了。 因此，他们的结果为0。（我们在初始化的时候就初始化为0了）。

（2）python代码：

class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        n = len(T)
        ret = [0]*n # 初始化结果列表为0
        stack = [] # 单调栈
        for i in range(n):
            while stack and T[stack[-1]]<T[i]: # 当前元素比栈顶元素大
                pre_index = stack.pop() # 栈顶元素为我们要 求的 之前元素的下标
                ret[pre_index] = i - pre_index # 当前元素-栈顶元素
            stack.append(i) # 切记存放下标
        return ret

（3）C++代码：

class Solution {
     
public:
    vector<int> dailyTemperatures(vector<int>& T) {
     
        int n = T.size();
        vector<int> ret(n, 0); //初始化为0
        stack<int> s; //单调栈
        for(int i=0;i<n;++i)
        {
     
            while(!s.empty() && T[s.top()]<T[i])
            {
     
                int pre_index = s.top(); //栈顶元素为我们要 求的 之前元素的下标
                ret[pre_index] = i - pre_index; //计算距离
                s.pop();
            }
            s.push(i); //每个元素的下标入栈
        }
        return ret;
    }
};

4、总结：

一般来说，求一个数组的下一个更大元素，就使用 单调栈 来做，因此，要是遇到了类似的题目，可以直接上模板：

（1）for循环遍历这个数组；
（2）while循环遍历栈，要是栈顶元素对应的值小，则出栈，直到不小为止；
（3）遍历栈的时候，记得保存找到的值；
（4）入栈当前元素的下标。

一般来说栈中存放的都是下标，而不是值，这样泛化性更好！！！