机器学习(三)线性判别准则与线性分类编程实践
文章目录
-
- 1. 线性判别准则(LDA)
-
- 1.1 什么是LDA?
- 1.2 Sklearn实现LDA算法
- 2. 线性分类算法(SVM)
-
- 2.1 什么是SVM
- 2.2 Sklearn实现SVM线性分类算法
- 3. 总结
- 4. 参考文章
- 5. 代码下载
1. 线性判别准则(LDA)
1.1 什么是LDA?
不同于PCA方差最大化理论,线性判别分析(linear discriminant analysis,LDA)是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学,模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理,使得同一类数据尽可能的紧凑,不同类的数据尽可能分散。因此,LDA算法是一种有监督的机器学习算法。同时,LDA有如下两个假设:
(1) 原始数据根据样本均值进行分类。
(2) 不同类的数据拥有相同的协方差矩阵。
当然,在实际情况中,不可能满足以上两个假设。但是当数据主要是由均值来区分的时候,LDA一般都可以取得很好的效果。
基本思想: 将原始数据投影至低维空间,尽量使同一类的数据聚集,不同类的数据尽可能分散。
**计算步骤: **
- 计算数据集中不同类别数据的 d 维均值向量。
- 计算散布矩阵,包括类间、类内散布矩阵。
- 计算散布矩阵的特征向量 e1,e2,…,ed 和对应的特征值 λ1,λ2,…,λd。
- 将特征向量按特征值大小降序排列,然后选择前 k 个最大特征值对应的特征向量,组建一个 d×k 维矩阵——即每一列就是一个特征向量。
- 用这个 d×k-维特征向量矩阵将样本变换到新的子空间。这一步可以写作矩阵乘法 Y=X×W 。 X 是 n×d 维矩阵,表示 n 个样本; y 是变换到子空间后的 n×k 维样本。
1.2 Sklearn实现LDA算法
- 导入包
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 导入大量Sklearn库相关包
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
- 定义可视化函数
#可视化函数
def plot_decision_regions(x, y, classifier, resolution=0.02):
markers = ['s', 'x', 'o', '^', 'v']
colors = ['r', 'g', 'b', 'gray', 'cyan']
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1
x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
z = z.reshape(xx1.shape)
plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)
for idx, cc in enumerate(np.unique(y)):
plt.scatter(x=x[y == cc, 0],
y=x[y == cc, 1],
alpha=0.6,
c=cmap(idx),
edgecolor='black',
marker=markers[idx],
label=cc)
- 拟合数据
#数据集来源
data = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
#切割数据集
#x数据
#y标签
x, y = data.iloc[:, 1:].values, data.iloc[:, 0].values
#按照8:2比例划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)
#标准化单位方差
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.fit_transform(x_test)
lda = LDA(n_components=2)
lr = LogisticRegression()
#训练
x_train_lda = lda.fit_transform(x_train_std, y_train)
#测试
x_test_lda = lda.fit_transform(x_test_std, y_test)
#拟合
lr.fit(x_train_lda, y_train)
- 展示结果
# 画图高宽,像素
plt.figure(figsize=(6, 7), dpi=100)
plot_decision_regions(x_train_lda, y_train, classifier=lr)
plt.show()
2. 线性分类算法(SVM)
2.1 什么是SVM
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。
SVM使用铰链损失函数(hinge loss)计算经验风险(empirical risk)并在求解系统中加入了正则化项以优化结构风险(structural risk),是一个具有稀疏性和稳健性的分类器 [2] 。SVM可以通过核方法(kernel method)进行非线性分类,是常见的核学习(kernel learning)方法之一。
将实例的特征向量(以二维为例)映射为空间中的一些点,如下图的实心点和空心点,它们属于不同的两类。SVM 的目的就是想要画出一条线,以“最好地”区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。
2.2 Sklearn实现SVM线性分类算法
- 导入相关包
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
- 加载数据
#使用生成的数据
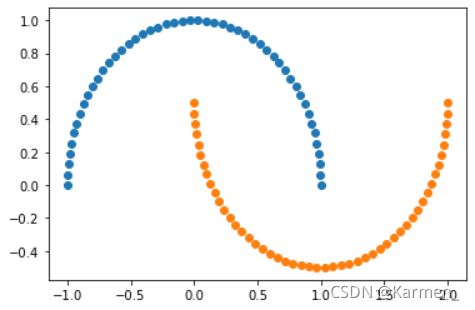
X, y = datasets.make_moons()
#展示数据
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
- 修改数据
#随机生成噪声点,random_state是随机种子,noise是方差
X, y = datasets.make_moons(noise=0.15,random_state=520)
#展示处理过后的数据
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
- 定义函数
#非线性SVM分类,当degree为0表示线性
def PolynomialSVC(degree,C=1.0):
return Pipeline([
("poly",PolynomialFeatures(degree=degree)),#生成多项式
("std_scaler",StandardScaler()),#标准化
("linearSVC",LinearSVC(C=C))#最后生成svm
])
#绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
#核函数
def PolynomialKernelSVC(degree,C=1.0):
return Pipeline([
("std_scaler",StandardScaler()),
("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
])
#高斯核函数
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
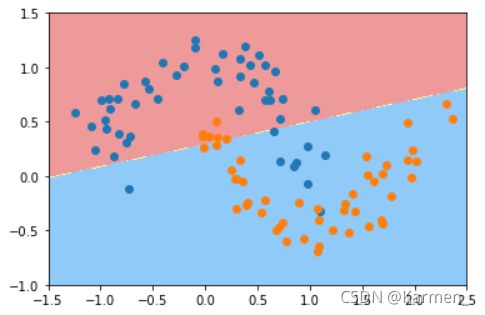
- 线性处理
#线性处理,c=1
poly_svc = PolynomialSVC(degree=1,C=1)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
#线性处理,c=500
poly_svc = PolynomialSVC(degree=1,C=500)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
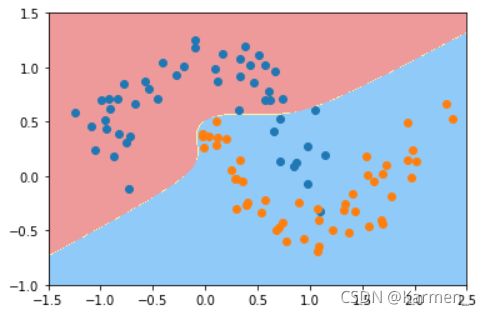
- 非线性处理
#非线性处理
poly_kernel_svc = PolynomialSVC(degree=10,C=1)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
#非线性处理
poly_kernel_svc = PolynomialSVC(degree=10,C=100)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
- 核函数处理
#核函数处理
poly_kernel_svc = PolynomialKernelSVC(degree=10)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
#核函数处理
poly_kernel_svc = PolynomialKernelSVC(degree=50)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
- 高斯核函数处理
#高斯核处理 参数为2
svc = RBFKernelSVC(2)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
#高斯核处理 参数为20
svc = RBFKernelSVC(20)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
#高斯核处理 参数为200
svc = RBFKernelSVC(100)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
3. 总结
LDA: 假设:数据是正态分布的。如果各组具有不同的协方差矩阵,则所有组的分布均相同,LDA变为二次判别分析。在实际满足所有假设的情况下,LDA是最好的判别器。顺便说一下,QDA是一个非线性分类器。
SVM: 概括最佳分离超平面(OSH)。OSH假定所有组都是完全可分离的,SVM利用“松弛变量”允许组之间有一定程度的重叠。SVM完全不假设数据,这意味着它是一种非常灵活的方法。另一方面,与LDA相比,灵活性通常使解释SVM分类器的结果更加困难。
SVM分类是一个优化问题,LDA具有解析解决方案。SVM的优化问题具有对偶和原始公式,使用户可以根据数据上最可行的方法在数据点数或变量数上进行优化。SVM还可以利用内核将SVM分类器从线性分类器转换为非线性分类器。使用您喜欢的搜索引擎搜索“ SVM内核技巧”,以了解SVM如何利用内核来转换参数空间。
LDA利用整个数据集来估计协方差矩阵,因此有些容易出现异常值。SVM在数据的一个子集上进行了优化,这些数据是位于分隔边距上的那些数据点。用于优化的数据点称为支持向量,因为它们确定SVM如何区分组,从而支持分类。
即LDA是可生成的,SVM是可区分的。
4. 参考文章
百度百科:线性判别分析
百度百科:支持向量机
知乎-超爱学习:机器学习-LDA(线性判别降维算法)
QAStack-SVM和LDA有什么区别?
醉意丶千层梦:基于Sklearn实现LDA算法
醉意丶千层梦:基于Sklearn实现SVM算法
陈一月的编程岁月: 基于jupyter notebook的python编程-----支持向量机学习二(SVM处理线性[鸢尾花数据集]和非线性数据集[月亮数据集])
5. 代码下载
点我提取码0000