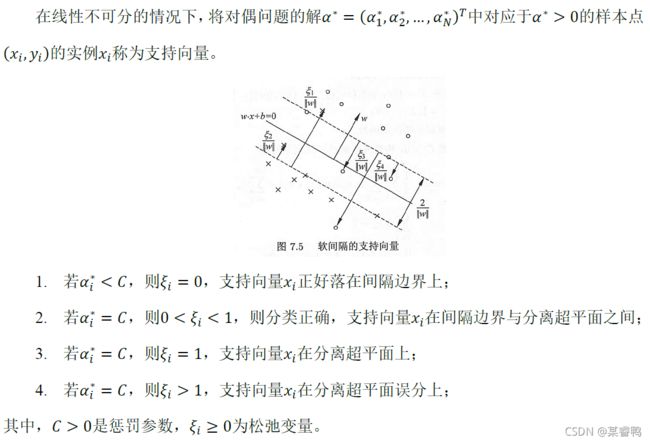
支持向量机SVM及python实现
支持向量机
SVM是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;核技巧使他成为实质上的非线性分类器。SVM是求解凸二次规划的问题最优化问题。
SVM可分为:
- 线性可分支持向量机:数据线性可分,通过硬间隔最大化,学习一个线性分类器。
- 线性支持向量机:数据近似线性可分,通过软间隔最大化,学习一个分类器。
- 非线性支持向量机:数据线性不可分,通过使用核技巧及软间隔最大化。
技术:
- SMO
- 核函数
- 序列最小最优化
输入空间为欧氏空间或这是离散集合、特征空间是希尔伯特空间(在一个实向量空间或复向量空间H上的给定的内积 < x , y > < x,y > <x,y>可以按照如下的方式导出一个范数(norm): ∣ x ∣ = < x , y > |x|=\sqrt{
一、线性可分支持向量机
1. 函数间隔和几何间隔

函数间隔可以表示分类预测的正确性及确信度。但是选择分离超平面时,只有函数间隔还不够。因为函数间隔改变时,超平面有可能没有改变。所以我们可以对分离超平面的法向量ω加些约束,如规范化, ∣ ∣ ω ∣ ∣ = 1 ||ω||=1 ∣∣ω∣∣=1,使得间隔是确定的。这时函数间隔变为几何间隔。

从函数间隔与几何间隔的定义可知,函数间隔和几何间隔有下面的关系:
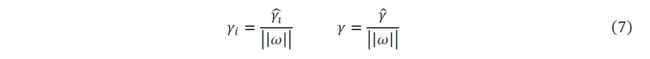
如果 ∣ ∣ ω ∣ ∣ = 1 ||ω||=1 ∣∣ω∣∣=1,那么函数间隔和几何间隔相等。如果超平面参数 ω ω ω和 b b b成比例的改变(超平面没有改变),函数间隔也按此比例改变,而几何间隔不变。
2. 间隔最大化
间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据集进行分类。也就是说,不仅将正负实例点分开,而且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开。这样的超平面应该对位置的新实例有很好的分类预测能力。




def _f(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
def _KKT(self, i):
y_f = self._f(i) * self.Y[i]
if not (self.alpha[i] >0):
return False
elif not(y_f>=0):
return False
elif not(self.alpha[0]*y_f == 0):
return False
return True
KKT条件详解【点击即可阅读】
二、 线性支持向量机
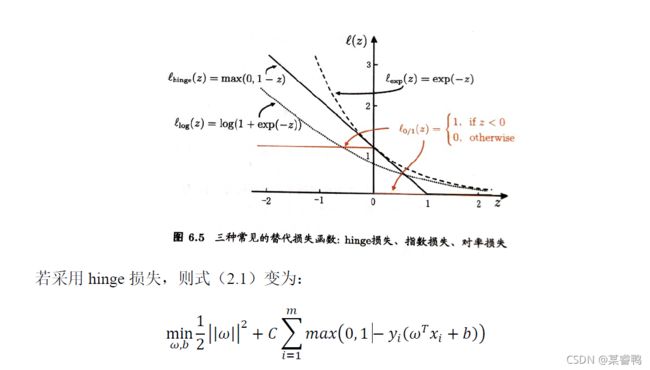
如何使用SVM处理线性不可分问题呢?这就需要修改硬间隔最大化,使其成为软间隔最大化。
软间隔的优化目标可写为:




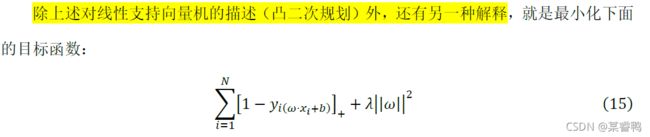


三、非线性支持向量机
1. 核技巧
用线性分类方法解决非线性分类问题分为两步:首先是用一个变换将原空间的数据映射到新空间;然后在新空间利用线性分类学习方法从训练数据中学习分类模型。



2. 正定核
不用构造映射函数 ϕ ( ) \phi() ϕ(x)能否直接判断一个给定的函数 K ( x , z ) K(x,z) K(x,z)是不是核函数? 通常所说的核函数指的是正定核函数。

3. 常用核函数
特征空间的好坏对支持向量机的性能至关重要。需要注意的是,在不知道特征映射空间的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式的定义了这个特征空间。于是,“核函数选择”成为支持向量机的最大变数。

def kernel_fuc(x, x2, kernel_Type):
"""
核函数
:param x: 支持向量的特征
:param x2: 某一例的特征
:param kernel_Type: 核函数类型和相应参数
:return:
"""
m, n = x.shape
K = np.mat(np.zeros((m, 1)))
if kernel_Type[0] == "line": # 线性核
K = x * x2.T
elif kernel_Type[0] == "radial": # 高斯核
for j in range(m):
deltaRow = x[j, :] - x2
# print(deltaRow.T)
try:
K[j] = deltaRow * deltaRow.T
except:
print(deltaRow)
K = np.exp(K / (-2 * kernel_Type[1] ** 2)) # 返回生成的结果
elif kernel_Type[0] == "Sigmoid": # Sigmoid核
K = np.tanh(kernel_Type[1] * x * x2.T + kernel_Type[2])
elif kernel_Type[0] == "Laplace": # 拉普拉斯核
for j in range(m):
deltaRow = x[j, :] - x2
K[j] = deltaRow * deltaRow.T
K = np.exp(K / (-1 * kernel_Type[1]))
elif kernel_Type[0] == "poly":
K = x * x2.T
K = K ** kernel_Type[1]
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
4. 非线性支持向量机
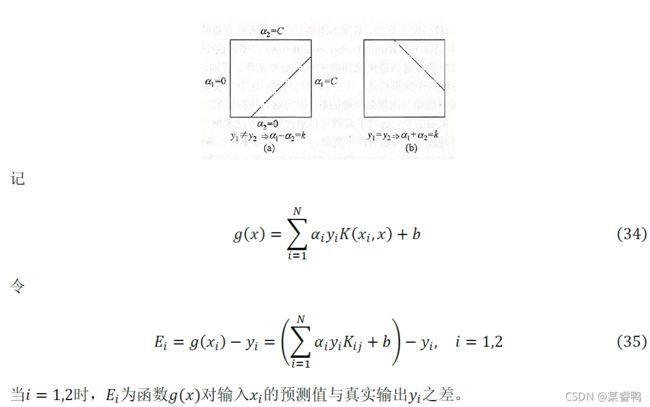
四、 序列最小最优化算法
当训练样本容量很大时,这些算法往往变得非常低效,以致无法使用。所以,如何高效地实现支持向量机学习成为一个重要的问题。本节讲述序列最小优化算法(SMO)。
SMO算法要解如下凸二次规划的对偶问题:
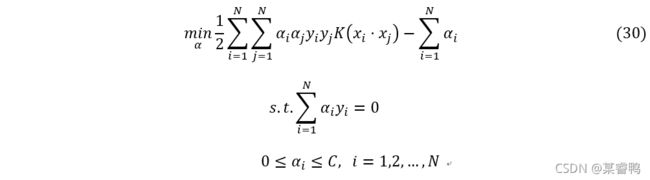

1. 两个变量二次规划的求解方法
def calcEk(self, i):
# 计算Ek(参考《统计学习方法(第二版)》p145公式7.105)
# print(self.alphas)
# print(self.y)
# print(np.shape(self.alphas))
# print(np.shape(self.y))
fXk = float(np.multiply(self.alphas, self.y).T * self.Kernel[:, i] + self.b)
Ek = fXk - float(self.y[i])
return Ek
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E1 - E2) / eta
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] *(self.alpha[i2] - alpha2_new)
def _compare(self, _alpha, L, H):
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha
2. 变量的选择方法
SMO算法在每个子问题中选择两个变量优化,其中至少一个变量是违反KKT条件的。



def inner(self, i):
"""
首先检验ai是否满足KKT条件,如果不满足,随机选择aj进行优化,更新ai,aj,b值
"""
Ei = self.calcEk(i)
if ((self.y[i] * Ei < -self.eps) and (self.alphas[i] < self.C)) or (
(self.y[i] * Ei > self.eps) and (self.alphas[i] > 0)):
# 检验这行数据是否符合KKT条件 参考《统计学习方法(第二版)》p145公式7.111-113
# 阿喂,这里方法是取了反的,就是不满足的话,才进来
j, Ej = self.selectJ(i, Ei)
alpha1old = self.alphas[i].copy()
alpha2old = self.alphas[j].copy()
# 以下参考《统计学习方法(第二版)》p144公式
if (self.y[i] != self.y[j]):
L = max(0, self.alphas[j] - self.alphas[i])
H = min(self.C, self.C + self.alphas[j] - self.alphas[i])
else:
L = max(0, self.alphas[j] - self.alphas[j] - self.C)
H = min(self.C, self.alphas[j] + self.alphas[i])
if L == H:
print("L==H")
return 0
# 参考《统计学习方法(第二版)》p145公式7.107
eta = 2.0 * self.Kernel[i, j] - self.Kernel[i, i] - self.Kernel[j, j]
if eta >= 0:
print("eta>=0")
return 0
# 参考《统计学习方法(第二版)》p145公式7.106
self.alphas[j] -= self.y[j] * (Ei - Ej) / eta
# 参考《统计学习方法(第二版)》p145公式7.108
self.alphas[j] = self.clipAlpha(self.alphas[j], H, L)
# 更新alphas[j]的缓存
self.updateEk(j)
# alpha变化大小阀值(自己设定)
if (abs(self.alphas[j] - alpha2old) < self.eps):
print("j not moving enough")
return 0
# 参考《统计学习方法(第二版)》p145公式7.109
self.alphas[i] += self.y[i] * self.y[j] * (alpha2old - self.alphas[j])
# 更新alphas[i]的缓存
self.updateEk(i)
# 求解b,参考《统计学习方法(第二版)》p148公式7.115
b1 = self.b - Ei - self.y[i] * (self.alphas[i] - alpha1old) * self.Kernel[i, i] - self.y[j] * (
self.alphas[j] - alpha2old) * self.Kernel[i, j]
# 求解b,参考《统计学习方法(第二版)》p148公式7.116
b2 = self.b - Ej - self.y[i] * (self.alphas[i] - alpha1old) * self.Kernel[i, j] - self.y[j] * (
self.alphas[j] - alpha2old) * self.Kernel[j, j]
if 0 < self.alphas[i] < self.C:
self.b = b1
elif 0 < self.alphas[j] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
return 1
else:
return 0
def SMO(self, X, y):
iter = 0 # 迭代次数
entireSet = True # 未知
alphaPairsChanged = 0 # alpha的改变量
while (iter < self.max_iter) and ((alphaPairsChanged > 0) or entireSet):
alphaPairsChanged = 0
if entireSet:
for i in range(self.m):
alphaPairsChanged += self.inner(i)
print("边界,迭代次数:%d 特征第%d行使得alpha改变,改变了%d" % (iter, i, alphaPairsChanged))
iter += 1
else:
# mat.A 将矩阵转换为数组类型(numpy 的narray)
nonBoundIs = np.nonzero((self.alphas.A > 0) * (self.alphas.A < self.C))[0]
for i in nonBoundIs:
# 遍历非边界的数值
alphaPairsChanged += self.inner(i)
print("非边界,迭代次数:%d 特征第%d行使得alpha改变,改变了%d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
print("当前迭代次数:%i" % iter)
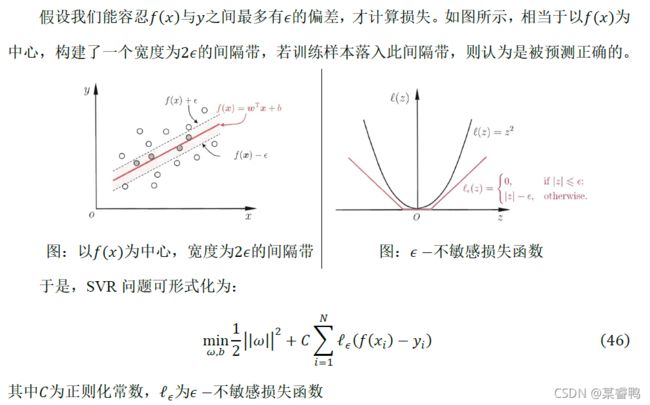
五、 支持向量回归
六、代码
代码1
本代码来自机器学习初学者(公众号)提供的代码。
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i, -1] == 0:
data[i, -1] = -1
# print(data)
return data[:, :2], data[:, -1]
class SVM:
def __init__(self, max_iter=100, kernel='linear'):
self.max_iter = max_iter
self._kernel = kernel
def init_args(self, features, labels):
self.m, self.n = features.shape
self.X = features
self.Y = labels
self.b = 0.0
# 将Ei保存在一个列表里
self.alpha = np.ones(self.m)
self.E = [self._E(i) for i in range(self.m)]
# 松弛变量
self.C = 1.0
def _KKT(self, i):
y_g = self._g(i) * self.Y[i]
if self.alpha[i] == 0:
return y_g >= 1
elif 0 < self.alpha[i] < self.C:
return y_g == 1
else:
return y_g <= 1
# g(x)预测值,输入xi(X[i])
def _g(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
# 核函数
def kernel(self, x1, x2):
if self._kernel == 'linear':
return sum([x1[k] * x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1) ** 2
return 0
# E(x)为g(x)对输入x的预测值和y的差
def _E(self, i):
return self._g(i) - self.Y[i]
def _init_alpha(self):
# 外层循环首先遍历所有满足0
index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
# 否则遍历整个训练集
non_satisfy_list = [i for i in range(self.m) if i not in index_list]
index_list.extend(non_satisfy_list)
for i in index_list:
if self._KKT(i):
continue
E1 = self.E[i]
# 如果E2是+,选择最小的;如果E2是负的,选择最大的
if E1 >= 0:
j = min(range(self.m), key=lambda x: self.E[x])
else:
j = max(range(self.m), key=lambda x: self.E[x])
return i, j
def _compare(self, _alpha, L, H):
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha
def fit(self, features, labels):
self.init_args(features, labels)
for t in range(self.max_iter):
# train
i1, i2 = self._init_alpha()
# 边界
if self.Y[i1] == self.Y[i2]:
L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
H = min(self.C, self.alpha[i1] + self.alpha[i2])
else:
L = max(0, self.alpha[i2] - self.alpha[i1])
H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])
E1 = self.E[i1]
E2 = self.E[i2]
# eta=K11+K22-2K12
eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
self.X[i2],
self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
if eta <= 0:
# print('eta <= 0')
continue
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
E1 - E2) / eta # 此处有修改,根据书上应该是E1 - E2,书上130-131页
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
self.alpha[i2] - alpha2_new)
b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b
if 0 < alpha1_new < self.C:
b_new = b1_new
elif 0 < alpha2_new < self.C:
b_new = b2_new
else:
# 选择中点
b_new = (b1_new + b2_new) / 2
# 更新参数
self.alpha[i1] = alpha1_new
self.alpha[i2] = alpha2_new
self.b = b_new
self.E[i1] = self._E(i1)
self.E[i2] = self._E(i2)
return 'train done!'
def predict(self, data):
r = self.b
for i in range(self.m):
r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
return 1 if r > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
result = self.predict(X_test[i])
if result == y_test[i]:
right_count += 1
return right_count / len(X_test)
def _weight(self):
# linear model
yx = self.Y.reshape(-1, 1) * self.X
self.w = np.dot(yx.T, self.alpha)
return self.w
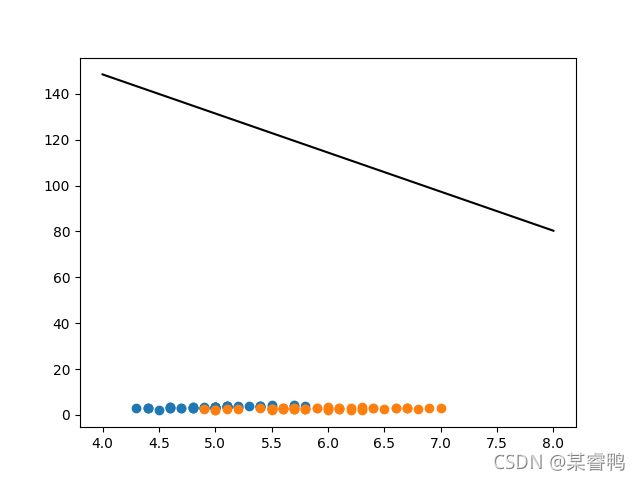
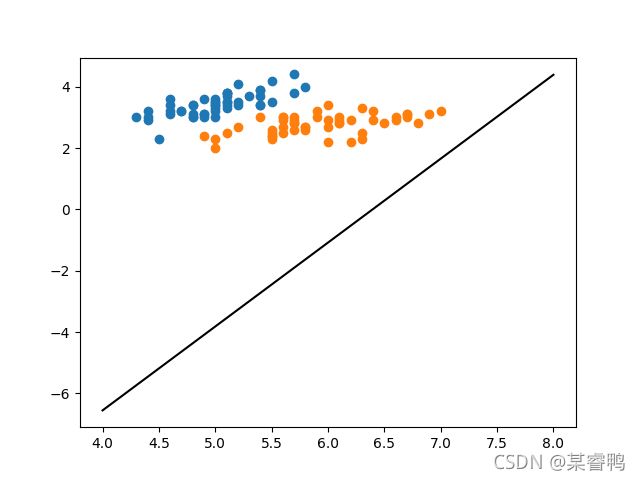
def PLT(self, X, y):
self.w = self._weight()
plt.scatter(X[:50, 0], X[:50, 1], label="0")
plt.scatter(X[50:, 0], X[50:, 1], label="1")
a = -self.w[0] / self.w[1]
xaxis = np.linspace(4, 8)
y_sep = a * xaxis - (self.b) / self.w[1]
plt.plot(xaxis, y_sep, 'k-')
plt.show()
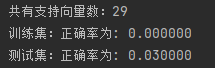
if __name__ == '__main__':
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
svm = SVM(max_iter=200)
svm.fit(X_train, y_train)
print(svm.score(X_test, y_test))
svm.PLT(X, y)
然后我就开始暴风哭泣,这是个什么人间疾苦,我的SVM怎么不是SVM,后来发下是选的核函数不太合适,修改完核函数就nice了,这里俺就不搞了,留给你们去搞
代码2
本代码是在我暴风哭泣之后,面向CSDN编程后得到的,原文链接:https://blog.csdn.net/NichChen/article/details/85329701
有自己加的一些注释,可视化有点不太会搞,如果有大佬会的话,可以教教俺,呜呜
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
def loadDataSet(filename):
"""
用于自建数据集,且标签为-1或1
:param filename:
:return:
"""
dataMat = []
labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat # 返回数据特征和数据类别
def create_data():
"""
用于已有数据集,且标签为0或1
"""
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
# print(df)
# print("----------------------------------------------")
data = np.array(df.iloc[:100, [0, 1, -1]])
# print(data)
# print("----------------------------------------------")
for i in range(len(data)):
if data[i, -1] == 0:
data[i, -1] = -1
# print(data)
return data[:, :2], data[:, -1]
class SVM():
def __init__(self, features, labels, eps=0.1, C=0.1, max_iter=100, kernel=['radial', 1.3]):
"""
模型参数初始化
:param features: 数据特征
:param labels: 标签
:param eps: 停止阀值
:param C: 惩罚因此,也称软间隔参数
:param max_iter: 最大迭代次数
:param kernel: 核函数
"""
self.X = features
self.y = labels
print(np.shape(self.y))
self.C = C
self.eps = eps
self.m = features.shape[0] # 数据行数
self.alphas = np.mat(np.zeros((self.m, 1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m, 2)))
self.max_iter = max_iter
self.kernel_Type = kernel
self.Kernel = np.mat(np.zeros((self.m, self.m)))
"""
如果这里使用:self.Kernel = np.zeros((self.m, self.m))
则会报错:
self.Kernel[:, i] = self.kernel_fuc(self.X, self.X[i, :], self.kernel_Type)
ValueError: could not broadcast input array from shape (100,1) into shape (100)
"""
for j in range(self.m):
"""
因为特征X在训练过程中是不会变化的,故可以提前算出
又因为SVM在计算时,每次都是\sum_{i=1}^N K(x_i,x_j) 所以可以直接输入全部的x与x_j进行求解
"""
self.Kernel[:, j] = self.kernel_fuc(self.X, self.X[j, :], self.kernel_Type)
@staticmethod
def kernel_fuc(x, x2, kernel_Type):
"""
核函数
:param x: 支持向量的特征
:param x2: 某一例的特征
:param kernel_Type: 核函数类型和相应参数
:return:
"""
m, n = x.shape
K = np.mat(np.zeros((m, 1)))
if kernel_Type[0] == "line": # 线性核
K = x * x2.T
elif kernel_Type[0] == "radial": # 高斯核
for j in range(m):
deltaRow = x[j, :] - x2
# print(deltaRow.T)
try:
K[j] = deltaRow * deltaRow.T
except:
print(deltaRow)
K = np.exp(K / (-2 * kernel_Type[1] ** 2)) # 返回生成的结果
elif kernel_Type[0] == "Sigmoid": # Sigmoid核
K = np.tanh(kernel_Type[1] * x * x2.T + kernel_Type[2])
elif kernel_Type[0] == "Laplace": # 拉普拉斯核
for j in range(m):
deltaRow = x[j, :] - x2
K[j] = deltaRow * deltaRow.T
K = np.exp(K / (-1 * kernel_Type[1]))
elif kernel_Type[0] == "poly":
K = x * x2.T
K = K ** kernel_Type[1]
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
def selectJrand(self, i):
j = i
while (j == i):
j = int(np.random.uniform(0, self.m))
return j
def selectJ(self, i, Ei):
# 随机选取aj,并返回其E值
maxK = -1
maxDeltaE = 0
Ej = 0
self.eCache[i] = [1, Ei]
validEcacheList = np.nonzero(self.eCache[:, 0].A)[0] # 返回矩阵中的非零位置的行数
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i:
continue
Ek = self.calcEk(k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK, maxDeltaE, Ej = k, deltaE, Ek
return maxK, Ej
else:
j = self.selectJrand(i)
Ej = self.calcEk(j)
return j, Ej
def calcEk(self, i):
# 计算Ek(参考《统计学习方法(第二版)》p145公式7.105)
# print(self.alphas)
# print(self.y)
# print(np.shape(self.alphas))
# print(np.shape(self.y))
fXk = float(np.multiply(self.alphas, self.y).T * self.Kernel[:, i] + self.b)
Ek = fXk - float(self.y[i])
return Ek
def clipAlpha(self, aj, H, L):
# 参考《统计学习方法(第二版)》p145公式7.108
if aj > H:
return H
if L > aj:
return L
return aj
def updateEk(self, k):
Ek = self.calcEk(k)
self.eCache[k] = [1, Ek]
def inner(self, i):
"""
首先检验ai是否满足KKT条件,如果不满足,随机选择aj进行优化,更新ai,aj,b值
"""
Ei = self.calcEk(i)
if ((self.y[i] * Ei < -self.eps) and (self.alphas[i] < self.C)) or (
(self.y[i] * Ei > self.eps) and (self.alphas[i] > 0)):
# 检验这行数据是否符合KKT条件 参考《统计学习方法(第二版)》p145公式7.111-113
# 阿喂,这里方法是取了反的,就是不满足的话,才进来
j, Ej = self.selectJ(i, Ei)
alpha1old = self.alphas[i].copy()
alpha2old = self.alphas[j].copy()
# 以下参考《统计学习方法(第二版)》p144公式
if (self.y[i] != self.y[j]):
L = max(0, self.alphas[j] - self.alphas[i])
H = min(self.C, self.C + self.alphas[j] - self.alphas[i])
else:
L = max(0, self.alphas[j] - self.alphas[j] - self.C)
H = min(self.C, self.alphas[j] + self.alphas[i])
if L == H:
print("L==H")
return 0
# 参考《统计学习方法(第二版)》p145公式7.107
eta = 2.0 * self.Kernel[i, j] - self.Kernel[i, i] - self.Kernel[j, j]
if eta >= 0:
print("eta>=0")
return 0
# 参考《统计学习方法(第二版)》p145公式7.106
self.alphas[j] -= self.y[j] * (Ei - Ej) / eta
# 参考《统计学习方法(第二版)》p145公式7.108
self.alphas[j] = self.clipAlpha(self.alphas[j], H, L)
# 更新alphas[j]的缓存
self.updateEk(j)
# alpha变化大小阀值(自己设定)
if (abs(self.alphas[j] - alpha2old) < self.eps):
print("j not moving enough")
return 0
# 参考《统计学习方法(第二版)》p145公式7.109
self.alphas[i] += self.y[i] * self.y[j] * (alpha2old - self.alphas[j])
# 更新alphas[i]的缓存
self.updateEk(i)
# 求解b,参考《统计学习方法(第二版)》p148公式7.115
b1 = self.b - Ei - self.y[i] * (self.alphas[i] - alpha1old) * self.Kernel[i, i] - self.y[j] * (
self.alphas[j] - alpha2old) * self.Kernel[i, j]
# 求解b,参考《统计学习方法(第二版)》p148公式7.116
b2 = self.b - Ej - self.y[i] * (self.alphas[i] - alpha1old) * self.Kernel[i, j] - self.y[j] * (
self.alphas[j] - alpha2old) * self.Kernel[j, j]
if 0 < self.alphas[i] < self.C:
self.b = b1
elif 0 < self.alphas[j] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
return 1
else:
return 0
def SMO(self, X, y):
iter = 0 # 迭代次数
entireSet = True # 未知
alphaPairsChanged = 0 # alpha的改变量
while (iter < self.max_iter) and ((alphaPairsChanged > 0) or entireSet):
alphaPairsChanged = 0
if entireSet:
for i in range(self.m):
alphaPairsChanged += self.inner(i)
print("边界,迭代次数:%d 特征第%d行使得alpha改变,改变了%d" % (iter, i, alphaPairsChanged))
iter += 1
else:
# mat.A 将矩阵转换为数组类型(numpy 的narray)
nonBoundIs = np.nonzero((self.alphas.A > 0) * (self.alphas.A < self.C))[0]
for i in nonBoundIs:
# 遍历非边界的数值
alphaPairsChanged += self.inner(i)
print("非边界,迭代次数:%d 特征第%d行使得alpha改变,改变了%d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
print("当前迭代次数:%i" % iter)
def fit(self, X, y):
self.SMO(X, y) # 通过SMO算法得到b和alpha
self.svInd = np.nonzero(self.alphas)[0] # 选取不为0数据的行数(也就是支持向量)
self.sVs = X[self.svInd] # 支持向量的特征数据
self.ySv = y[self.svInd] # 支持向量的类别(1或-1)
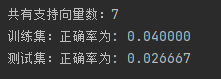
print("共有支持向量数:%d" % np.shape(self.sVs)[0]) # 打印出共有多少的支持向量
print("训练集:", end="")
self.score(X, y)
def score(self, X, y):
errcnt = 0
for i in range(len(X)):
# 将支持向量转化为核函数
try:
kernelEval = self.kernel_fuc(self.sVs, X[i, :], self.kernel_Type)
predict = kernelEval.T * np.multiply(self.ySv, self.alphas[self.svInd]) + self.b
if np.sign(predict) != np.sign(y[i]):
# sign函数 -1 if x < 0, 0 if x==0, 1 if x > 0
errcnt += 1
except:
print("self.sVs=", self.sVs)
print("i:=", i)
print("X.shape()=", X.shape)
print("self.kernerl_Type=", self.kernel_Type)
print("正确率为: %f" % (float(errcnt) / self.m)) # 打印出错误率
def _weight(self):
# linear model
print(self.y)
print(X)
yx = self.y.reshape(-1, 1) * self.X
self.w = np.dot(yx.T, self.alphas)
return self.w
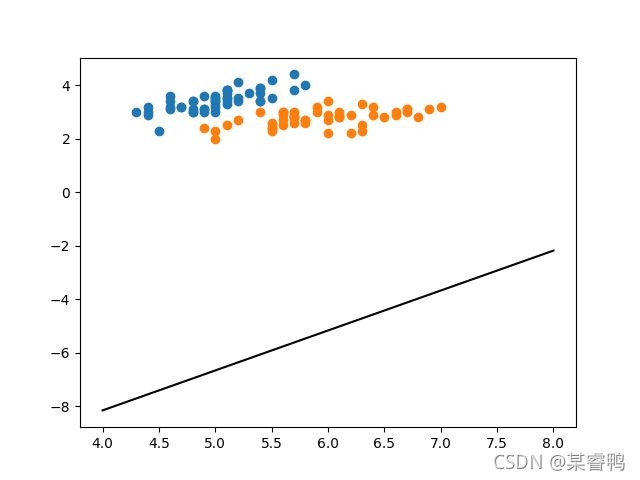
def PLT(self, X, y):
self.w = self._weight()
plt.scatter(X[:50, 0], X[:50, 1], label="0")
plt.scatter(X[50:, 0], X[50:, 1], label="1")
a = -self.w[0] / self.w[1]
xaxis = np.linspace(4, 8)
y_sep = a * xaxis - (self.b) / self.w[1]
plt.plot(xaxis, y_sep, 'k-')
plt.show()
if __name__ == '__main__':
filename_traindata = "D:/python/meaching learning/支持向量机/train.txt"
filename_testdata = "D:/python/meaching learning/支持向量机/test.txt"
X_train, y_train = loadDataSet(filename_traindata)
X_test, y_test = loadDataSet(filename_testdata)
# X, y = create_data()
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train = np.mat(X_train)
y_train = np.mat(y_train).transpose()
X_test = np.mat(X_test)
y_test = np.mat(y_test).transpose()
print(np.shape(y_train))
svm = SVM(features=X_train, labels=y_train, C=200, eps=0.0001, max_iter=10000, kernel=['radial', 1.3])
print(np.shape(svm.y))
svm.fit(X_train, y_train)
print("测试集:", end="")
svm.score(X_test, y_test)
X = np.array(np.vstack((X_train, X_test)))
y = np.array(np.vstack((y_train, y_test)))
# svm.PLT(X, y)
数据集:
train.txt
-0.214824 0.662756 -1.000000
-0.061569 -0.091875 1.000000
0.406933 0.648055 -1.000000
0.223650 0.130142 1.000000
0.231317 0.766906 -1.000000
-0.748800 -0.531637 -1.000000
-0.557789 0.375797 -1.000000
0.207123 -0.019463 1.000000
0.286462 0.719470 -1.000000
0.195300 -0.179039 1.000000
-0.152696 -0.153030 1.000000
0.384471 0.653336 -1.000000
-0.117280 -0.153217 1.000000
-0.238076 0.000583 1.000000
-0.413576 0.145681 1.000000
0.490767 -0.680029 -1.000000
0.199894 -0.199381 1.000000
-0.356048 0.537960 -1.000000
-0.392868 -0.125261 1.000000
0.353588 -0.070617 1.000000
0.020984 0.925720 -1.000000
-0.475167 -0.346247 -1.000000
0.074952 0.042783 1.000000
0.394164 -0.058217 1.000000
0.663418 0.436525 -1.000000
0.402158 0.577744 -1.000000
-0.449349 -0.038074 1.000000
0.619080 -0.088188 -1.000000
0.268066 -0.071621 1.000000
-0.015165 0.359326 1.000000
0.539368 -0.374972 -1.000000
-0.319153 0.629673 -1.000000
0.694424 0.641180 -1.000000
0.079522 0.193198 1.000000
0.253289 -0.285861 1.000000
-0.035558 -0.010086 1.000000
-0.403483 0.474466 -1.000000
-0.034312 0.995685 -1.000000
-0.590657 0.438051 -1.000000
-0.098871 -0.023953 1.000000
-0.250001 0.141621 1.000000
-0.012998 0.525985 -1.000000
0.153738 0.491531 -1.000000
0.388215 -0.656567 -1.000000
0.049008 0.013499 1.000000
0.068286 0.392741 1.000000
0.747800 -0.066630 -1.000000
0.004621 -0.042932 1.000000
-0.701600 0.190983 -1.000000
0.055413 -0.024380 1.000000
0.035398 -0.333682 1.000000
0.211795 0.024689 1.000000
-0.045677 0.172907 1.000000
0.595222 0.209570 -1.000000
0.229465 0.250409 1.000000
-0.089293 0.068198 1.000000
0.384300 -0.176570 1.000000
0.834912 -0.110321 -1.000000
-0.307768 0.503038 -1.000000
-0.777063 -0.348066 -1.000000
0.017390 0.152441 1.000000
-0.293382 -0.139778 1.000000
-0.203272 0.286855 1.000000
0.957812 -0.152444 -1.000000
0.004609 -0.070617 1.000000
-0.755431 0.096711 -1.000000
-0.526487 0.547282 -1.000000
-0.246873 0.833713 -1.000000
0.185639 -0.066162 1.000000
0.851934 0.456603 -1.000000
-0.827912 0.117122 -1.000000
0.233512 -0.106274 1.000000
0.583671 -0.709033 -1.000000
-0.487023 0.625140 -1.000000
-0.448939 0.176725 1.000000
0.155907 -0.166371 1.000000
0.334204 0.381237 -1.000000
0.081536 -0.106212 1.000000
0.227222 0.527437 -1.000000
0.759290 0.330720 -1.000000
0.204177 -0.023516 1.000000
0.577939 0.403784 -1.000000
-0.568534 0.442948 -1.000000
-0.011520 0.021165 1.000000
0.875720 0.422476 -1.000000
0.297885 -0.632874 -1.000000
-0.015821 0.031226 1.000000
0.541359 -0.205969 -1.000000
-0.689946 -0.508674 -1.000000
-0.343049 0.841653 -1.000000
0.523902 -0.436156 -1.000000
0.249281 -0.711840 -1.000000
0.193449 0.574598 -1.000000
-0.257542 -0.753885 -1.000000
-0.021605 0.158080 1.000000
0.601559 -0.727041 -1.000000
-0.791603 0.095651 -1.000000
-0.908298 -0.053376 -1.000000
0.122020 0.850966 -1.000000
-0.725568 -0.292022 -1.000000
test.txt
0.676771 -0.486687 -1.000000
0.008473 0.186070 1.000000
-0.727789 0.594062 -1.000000
0.112367 0.287852 1.000000
0.383633 -0.038068 1.000000
-0.927138 -0.032633 -1.000000
-0.842803 -0.423115 -1.000000
-0.003677 -0.367338 1.000000
0.443211 -0.698469 -1.000000
-0.473835 0.005233 1.000000
0.616741 0.590841 -1.000000
0.557463 -0.373461 -1.000000
-0.498535 -0.223231 -1.000000
-0.246744 0.276413 1.000000
-0.761980 -0.244188 -1.000000
0.641594 -0.479861 -1.000000
-0.659140 0.529830 -1.000000
-0.054873 -0.238900 1.000000
-0.089644 -0.244683 1.000000
-0.431576 -0.481538 -1.000000
-0.099535 0.728679 -1.000000
-0.188428 0.156443 1.000000
0.267051 0.318101 1.000000
0.222114 -0.528887 -1.000000
0.030369 0.113317 1.000000
0.392321 0.026089 1.000000
0.298871 -0.915427 -1.000000
-0.034581 -0.133887 1.000000
0.405956 0.206980 1.000000
0.144902 -0.605762 -1.000000
0.274362 -0.401338 1.000000
0.397998 -0.780144 -1.000000
0.037863 0.155137 1.000000
-0.010363 -0.004170 1.000000
0.506519 0.486619 -1.000000
0.000082 -0.020625 1.000000
0.057761 -0.155140 1.000000
0.027748 -0.553763 -1.000000
-0.413363 -0.746830 -1.000000
0.081500 -0.014264 1.000000
0.047137 -0.491271 1.000000
-0.267459 0.024770 1.000000
-0.148288 -0.532471 -1.000000
-0.225559 -0.201622 1.000000
0.772360 -0.518986 -1.000000
-0.440670 0.688739 -1.000000
0.329064 -0.095349 1.000000
0.970170 -0.010671 -1.000000
-0.689447 -0.318722 -1.000000
-0.465493 -0.227468 -1.000000
-0.049370 0.405711 1.000000
-0.166117 0.274807 1.000000
0.054483 0.012643 1.000000
0.021389 0.076125 1.000000
-0.104404 -0.914042 -1.000000
0.294487 0.440886 -1.000000
0.107915 -0.493703 -1.000000
0.076311 0.438860 1.000000
0.370593 -0.728737 -1.000000
0.409890 0.306851 -1.000000
0.285445 0.474399 -1.000000
-0.870134 -0.161685 -1.000000
-0.654144 -0.675129 -1.000000
0.285278 -0.767310 -1.000000
0.049548 -0.000907 1.000000
0.030014 -0.093265 1.000000
-0.128859 0.278865 1.000000
0.307463 0.085667 1.000000
0.023440 0.298638 1.000000
0.053920 0.235344 1.000000
0.059675 0.533339 -1.000000
0.817125 0.016536 -1.000000
-0.108771 0.477254 1.000000
-0.118106 0.017284 1.000000
0.288339 0.195457 1.000000
0.567309 -0.200203 -1.000000
-0.202446 0.409387 1.000000
-0.330769 -0.240797 1.000000
-0.422377 0.480683 -1.000000
-0.295269 0.326017 1.000000
0.261132 0.046478 1.000000
-0.492244 -0.319998 -1.000000
-0.384419 0.099170 1.000000
0.101882 -0.781145 -1.000000
0.234592 -0.383446 1.000000
-0.020478 -0.901833 -1.000000
0.328449 0.186633 1.000000
-0.150059 -0.409158 1.000000
-0.155876 -0.843413 -1.000000
-0.098134 -0.136786 1.000000
0.110575 -0.197205 1.000000
0.219021 0.054347 1.000000
0.030152 0.251682 1.000000
0.033447 -0.122824 1.000000
-0.686225 -0.020779 -1.000000
-0.911211 -0.262011 -1.000000
0.572557 0.377526 -1.000000
-0.073647 -0.519163 -1.000000
-0.281830 -0.797236 -1.000000
-0.555263 0.126232 -1.000000
Pdf版:
链接:https://pan.baidu.com/s/1dzNouQBkdRja9rgWWoQV0g
提取码:RRTX