对抗样本(一)以综述入门
文章目录
- 一、论文相关信息
-
- 1.论文题目
- 2.论文时间
- 3.论文文献
- 二、论文背景及简介
- 三、论文的主要内容
- 四、论文的安排
- 五、论文的主要内容
-
-
- Section Ⅱ 简介
- Section Ⅲ 术语介绍
- Section Ⅳ 对抗攻击方法
-
- [1、L-BFGS](https://arxiv.org/abs/1312.6199)
- **[2、Fast Gradient Sign Method (FGSM)](https://arxiv.org/abs/1412.6572)**
- [3、Basic Iterative Method (BIM)](https://arxiv.org/abs/1607.02533)
- 4、 Iterative Least-Likely Class Method (ILLC)
- 5、Jacobian-based Saliency Map Attack (JSMA)
- [6、DeepFool](https://arxiv.org/abs/1511.04599)
- 7、CPPN EA Fool
- 8、C&W’s Attack
- [9、Zeroth Order Optimization (ZOO)](https://arxiv.org/abs/1708.03999)
- 10、Universal Perturbation
- [11、One Pixel Attack](https://arxiv.org/abs/1710.08864)
- 12、Feature Adversary
- 13、Hot/Cold
- 14、Natural GAN
- 15、Model-based Ensembling Attack
- 16、Ground-Truth Attack
- Section Ⅴ 其他领域的对抗攻击示例
- Section Ⅵ 对抗防御方法
-
- 1、Network Distillation(网络蒸馏)
- 2、Adversarial (Re)training(对抗训练)
- 3、Adversarial Detecting(对抗识别)
- 4、Input Reconstruction(输入重建)
- 5、Classifier Robustifying(鲁棒的分类器)
- 6、Network Verificatio(网络验证)
- 7、Ensembling Defenses(集成防御)
- 8、对抗防御总结
- Section Ⅶ 挑战与讨论
-
- A、迁移性
- B、对抗样本的存在性
- C、鲁棒性评估
- Section Ⅷ 总结
-
一、论文相关信息
1.论文题目
Adversarial Examples: Attacks and Defenses for Deep Learning
2.论文时间
2017年
3.论文文献
https://arxiv.org/abs/1712.07107
二、论文背景及简介
随着深度学习的快速发展与巨大成功,深度学习被应用在许多对安全有严格要求的环境中。然而,深度神经网络近来被发现,对于精心设计好的输入样本,其是脆弱的,这种样本就被称为对抗样本。对抗样本对人类是很容易分辨的,但却能在测试或部署阶段,很容易的糊弄深度神经网络。当应用深度神经网络到对安全有严格要求的环境中时,处理对抗样本造成的脆弱性变成已成了一个重要的任务。因此对抗样本的攻击和防御吸引了很大的注意。
这是一篇17年的对抗样本的综述,用来对对抗样本领域的基本知识进行一定程度的了解。
注:篇幅较长。
三、论文的主要内容
1、系统的分析生成对抗样本的方法,在不同的维度对攻击方法进行分类,并用易懂的直观的方式展现出来
2、观察近来的一些生成对抗样本的方法以及他们的变量,使用已经提供的分类法来比较它们。同时,展示了强化学习、生成建模、人脸识别、目标检测、语义分割、自然语言处理和恶意软件检测等领域的应用实例
3、基于对抗性实例的可转移性、对抗性实例的存在性和深度神经网络的健壮性评价,概述了对抗性实例的主要挑战和潜在的未来研究方向。
PS:对抗样本的迁移性的含义:能够迷惑一个模型的对抗样本通常也能够迷惑另外一种结构的模型,即便那个模型用不同的训练集训练,甚至用不同的训练方法(CNN的对抗样本也能迷惑决策树)。
对抗样本的迁移效应使得黑箱对抗攻击成为可能。
四、论文的安排
Section Ⅱ:介绍了深度学习的技术、模型、数据集的背景,讨论了传统的机器学习中的对抗样本例子
Section Ⅲ:阐述了对抗样本的分类方法(对抗样本术语介绍)
Section Ⅳ:详尽阐述了这些生成对抗样本的方法(对抗攻击方法)
Section Ⅴ:讨论了对抗样本例子的应用(一些其他领域的对抗样本例子)
Section Ⅵ:相应的对抗样本例子的对策被讨论(对抗防御)
Section Ⅶ:讨论了目前的挑战和潜在的解决方案
Section Ⅷ:总结了工作
五、论文的主要内容
Section Ⅱ 简介
A. 简要的介绍了深度学习,包括深度学习的概念、结构、数据集
B. 简要的陈述了ML中的对抗样本及解决方案
Section Ⅲ 术语介绍
将生成对抗样本的方法按三个维度进行分类,威胁模型(threat model), 扰动(perturbation), 基准( benchmark)
A.Threat model
对其又分成四个方面adversarial falsification, adversary’s knowledge, adversarial specificity, and attack frequency
1、Adversarial Falsification
分成假正例攻击(False positive attacks)和假反例攻击(False negative attacks)
假正例攻击是生成一个反例,让模型误认为正例
假反例攻击是生成一个正例,让模型误认为反例
2、Adversary’s Knowledge
分成白盒攻击(White-box attacks)和黑盒攻击(Black-box attacks)
白盒攻击假定攻击者可以完全访问他们正在攻击的神经网络模型的结构和参数,包括训练数据,模型结构,超参数情况,层的数目,激活函数,模型权重等。
黑盒攻击假定攻击者不能访问他们正在攻击的神经网络模型的结构和参数,只知道模型的输出(label or condidnece)。白盒攻击样本可以通过一些方法转换成黑盒攻击的方式。
3、Adversarial Specificity
分成有目标攻击(Targeted attacks)和无目标攻击(Non-targeted attacks)
目标攻击是神经网络将生成的对抗样本分类成一个特定的类。目标攻击通常最大化目标类的可能性。
无目标攻击,只要神经网络判定的label与原label不同即认为攻击成功。无目标攻击中的对抗样本生成方式大致有两种,一为运行几个目标攻击,取最小的扰动的那一个为对抗样本;二为最小化正确的类的分类可能性。
4、Attack Frequency
分成有单步攻击(One-time attacks)和迭代攻击(Iterative attacks)
单步攻击,只需优化一次即可生成对抗样本
迭代攻击,迭代的进行优化来生成对抗样本。比单步攻击效果更好,但花费更多的计算时间。
B.Perturbation
分析了扰动的三个方面perturbation scope, perturbation limitation, and perturbation measurement
1、Perturbation scope
分成个体攻击(Individual attacks)和普适性攻击(Universal attacks)
个体攻击对于每一个不同的原始输入应用不同的扰动
普适性攻击对整个数据集应用一个通用的扰动
现在大多数的攻击策略都是个体攻击,但是普适性攻击会让部署到现实世界更加容易。
2、Perturbation limitation
分成优化扰动(Optimized Perturbation)和普适性攻击(Constraint Perturbation)
优化扰动是把扰动作为优化问题的目标。为了最小化扰动来让人类无法辨别出扰动
普适性攻击是将扰动作为优化问题的约束条件。只要求扰动足够小。
3、Perturbation measurement
分成lp measure和Psychometric perceptual adversarial similarity score (PASS)
l0 l2 l∞,是三种常用的评价标准。l0计算对抗样本中改变的像素的数目。l2测量对抗样本与原始样本的欧氏距离。l∞表示对抗样本中所有像素的最大改变值
PASS是一种新的评价标准,符合人类的感知
C.Perturbation
1、Datasets
MNIST, CIFAR-10, and ImageNet是3中最常用的数据集。MNIST, CIFAR-10因为简单且数目少,所以比较容易去攻击和防御。ImageNet是至今最好的数据集去评价对抗攻击。
1、Victim Models
LeNet, VGG, AlexNet, GoogLeNet, CaffeNet, and ResNet. 比较常用。
Section Ⅳ 对抗攻击方法
本节阐述了几个典型的生成对抗样本方法。通过这些方法来说明对抗攻击如何被提升,以及当时的SOTA的对抗攻击能达到什么程度。
在 以 下 的 公 式 中 , x 代 表 原 始 图 像 。 x ′ 代 表 对 抗 样 本 。 l 代 表 原 始 标 签 , l ’ 代 表 对 抗 样 本 的 标 签 。 η 代 表 扰 动 在以下的公式中,x代表原始图像。x'代表对抗样本。\\ l代表原始标签,l’代表对抗样本的标签。\\ \eta代表扰动 在以下的公式中,x代表原始图像。x′代表对抗样本。l代表原始标签,l’代表对抗样本的标签。η代表扰动
1、L-BFGS
Szegedy 等人在2014年首次提出了使用对抗样本攻击深度神经网络。他们通过L-BFGS 方法产生对抗样本,方法如下:
m i n x ′ c ∣ ∣ η ∣ ∣ + J θ ( x ′ , l ′ ) s . t . x ′ ∈ [ 0 , 1 ] min\ x'\ \ c||\eta||+J_\theta(x',l') \\ s.t. \ \ \ \ \ x' \in[0,1] min x′ c∣∣η∣∣+Jθ(x′,l′)s.t. x′∈[0,1]
为了找到适合的常量C,L-BFGS算法通过线性搜索C > 0的所有情况,找到C 的近似值。实验表明,生成的对抗样本也可以推广到不同的模型和不同的训练数据集中。
2、Fast Gradient Sign Method (FGSM)
L-BFGS方法中使用的线性搜索方法代价很高并且是不切实际的。Goodfellow等人提出了一种快速的方法,叫做FGSM。他们在每一个像素上仅仅执行了一步沿着梯度符号方向上的梯度更新。他们的扰动形式为
η = ϵ s i g n ( ▽ x J θ ( x , l ) ) ϵ 代 表 扰 动 的 大 小 \eta = \epsilon sign(\bigtriangledown_xJ_\theta(x,l)) \ \ \ \epsilon代表扰动的大小\\ η=ϵsign(▽xJθ(x,l)) ϵ代表扰动的大小
最后 x ′ = x + η \ \ x' = x + \eta x′=x+η 。这个扰动,是通过反向传播过程来计算的
作者发现,高维神经网络的线性部分无法抵抗对抗样本。因此,一些正则化可以被用于深度神经网络。且,预训练不能够增加网络的鲁棒性。FGSM是一种无目标攻击。
1、FGSM的改进方法之Fast Gradient Value method
在该改进方法中用 η = ▽ x J ( θ , x , l ) \ \eta=\bigtriangledown_x J(\theta,x,l) η=▽xJ(θ,x,l) 替换原来的扰动。由于该方法没有常量,所以会生成具有较大差异的图像。
2、FGSM的改进方法之One-step Target Class Method (OTCM)
在该方法中,作者认为单步攻击是很容易迁移但是也很容易防御。所以将动量的思想放入FGSM中,来迭代的生成对抗样本。每次迭代的梯度计算公式为:
g t + 1 = μ g t + ▽ x J θ ( x t ′ , l ) ∣ ∣ ▽ x J θ ( x t ′ , l ) ∣ ∣ g_{t+1} = \mu g_t + \frac{\bigtriangledown_xJ_\theta(x'_t,l)}{||\bigtriangledown_xJ_\theta(x'_t,l)||} gt+1=μgt+∣∣▽xJθ(xt′,l)∣∣▽xJθ(xt′,l)
然后,对抗样本通过公式 x t + 1 ′ = x t ′ + ϵ s i g n ( g t + 1 ) \ x'_{t+1} = x'_t + \epsilon sign(g_{t+1}) xt+1′=xt′+ϵsign(gt+1) 获得。该方法通过引入动量提高了攻击的有效性,通过使用单步攻击和压缩方法提高了其迁移性。
同时,该方法将FGSM拓展到了目标攻击,其公式如下:
x ′ = x − ϵ s i g n ( ▽ x J θ ( θ , x , l ′ ) ) x' = x - \epsilon sign(\bigtriangledown_xJ_\theta(\theta,x,l')) x′=x−ϵsign(▽xJθ(θ,x,l′))
3、FGSM的改进方法之RAND-FGSM
作者发现,因为gradient masking,FGSM对白盒攻击的鲁棒性更好。所以,作者提出了随机FGSM,在更新对抗样本时,对样本增加随机值来进行对抗样本的防御。公式如下:
x t m p = x + α ⋅ s i g n ( N ( 0 d , I d ) ) , x ′ = x t m p + ( ϵ − α ) ⋅ s i g n ( ▽ x t m p J ( x t m p , l ) ) 在 这 里 α , ϵ 时 变 量 , 并 且 α < ϵ x_{tmp} = x + \alpha·sign(N(0^d,I^d)),\\ x' = x_{tmp} + (\epsilon - \alpha)·sign(\bigtriangledown_{x_{tmp}}J(x_{tmp},l))\\ 在这里\alpha,\epsilon时变量,并且\alpha<\epsilon xtmp=x+α⋅sign(N(0d,Id)),x′=xtmp+(ϵ−α)⋅sign(▽xtmpJ(xtmp,l))在这里α,ϵ时变量,并且α<ϵ
3、Basic Iterative Method (BIM)
之前的方法是假定数据能够直接被送入神经网络中。然而,在很多情况下,人们只能依靠一些设备例如照相机、传感器来传送数据。Kurakin等人将对抗样本应用到现实世界中。他们对FGSM做了一点点小的改变,使用了一个更好的优化方式(多次迭代)。在每次迭代过程中,他们会限制像素值来避免过大。
C l i p x , ξ { x ′ } = m i n { 255 , x + ξ , m a x { 0 , x − ϵ , x ′ } } Clip_{x,\xi} \{x'\} = min\{255,x+\xi,max\{0,x-\epsilon,x'\}\} Clipx,ξ{ x′}=min{ 255,x+ξ,max{ 0,x−ϵ,x′}}
在这里 C l i p x , ξ { x ′ } \ Clip_{x,\xi} \{x'\} Clipx,ξ{ x′} 函数限制了在每次迭代过程中的对抗样本的改变的大小。对抗样本通过多次迭代产生:
x 0 = x , x n + 1 = C l i p x , ξ { x n + ϵ s i g n ( ▽ x J ( x n , y ) ) } x_0 = x,\\ x_{n+1} =Clip_{x,\xi} \{x_n + \epsilon sign(\bigtriangledown _xJ(x_n,y))\} x0=x,xn+1=Clipx,ξ{ xn+ϵsign(▽xJ(xn,y))}
4、 Iterative Least-Likely Class Method (ILLC)
该方法时BIM的拓展,将BIM拓展到了目标攻击,使用与原始标签最不像的类作为目标,通过最大化交叉熵损失函数的方法来实现。
x 0 = x , y L L = a r g m i n y { p ( y ∣ x ) } x n + 1 = C l i p x , ξ { x n + ϵ s i g n ( ▽ x J ( x n , y L L ) ) } x_0 = x,\\ y_{LL} = argmin_y\{p(y|x)\}\\ x_{n+1} =Clip_{x,\xi} \{x_n + \epsilon sign(\bigtriangledown _xJ(x_n,y_{LL}))\} x0=x,yLL=argminy{ p(y∣x)}xn+1=Clipx,ξ{ xn+ϵsign(▽xJ(xn,yLL))}
他们成功的用一张手机拍摄的精心制作的图片欺骗了神经网络。他们也发现FGSM对光转化的鲁棒性更好,而迭代性方法不能够抵挡光转化。
5、Jacobian-based Saliency Map Attack (JSMA)
Papernot等人计算了原始样本x的Jacobian矩阵,计算方法如下:
J F ( x ) = ∂ F ( x ) ∂ x = [ ∂ F j ( x ) ∂ x i ] i ∗ j J_F(x) = \frac{\partial F(x)}{\partial x} = [\frac{\partial F_j(x)}{\partial x_i}]_{i*j} JF(x)=∂x∂F(x)=[∂xi∂Fj(x)]i∗j
F \ F F表示第2层到最后一层神经网络(刚开始最后一层使用的logit,之后被修改成softmax)。
通过这种方法,他们发现样本x的输入特征会对输出有着最显著的影响。那么,一个被设计好的小的扰动就能够引起输出的较大改变,这样,一个小的特征的改变就能够欺骗神经网络。
然后,作者定义了两个对抗性的saliency maps来选择在每次迭代过程中被创建的特征\像素。他们实现了97%的攻击成功率,每个样本却只改变了4.02%的的输入特征。但是,由于计算Jacobian矩阵很慢,因此这个方法运行的太慢了。
6、DeepFool
Moosavi-Dezfooli等人提出了DeppFool来寻找从原始输入到对抗样本决策边界最近的距离。为了克服高维中的非线性,他们用线性估计执行迭代攻击。从仿射分类器开始,他们发现,一个仿射分类器的最小扰动是到分类超平面 F = { x : w T x + b = 0 } \ F = \{x:w^T x +b =0\} F={ x:wTx+b=0}的距离。一个仿射分类器 f \ f f 的扰动可能是 η ∗ ( x ) = − f ( x ) ∣ ∣ w ∣ ∣ 2 w \ \eta^*(x) = -\frac{f(x)}{||w||^2}w η∗(x)=−∣∣w∣∣2f(x)w
如果分类器 f \ f f是一个二分类器,他们使用一种迭代的方法来估计扰动,并考虑在每次迭代过程中 f \ f f 是关于 x i \ x_i xi 是线性的。最小的扰动的计算方法如下:
a r g m i n η i ∣ ∣ η i ∣ ∣ 2 s . t . f ( x i ) + ▽ f ( x i ) T η i = 0 argmin_{\eta_i} \ \ \ ||\eta_i||_2\\ s.t.\ \ f(x_i)+\bigtriangledown f(x_i)^T \eta_i = 0 argminηi ∣∣ηi∣∣2s.t. f(xi)+▽f(xi)Tηi=0
这个结果可以通过找到最近的超平面的方法拓展到多分类任务。这也可以拓展到更普遍的$\ l_p $ 正则化。相比于FGSM和JSMA,DeepFool提供了更少的扰动。相比于JSMA,DeepFool降低了扰动的强度而不是选中的特征的数目。
7、CPPN EA Fool
Nguyen等人发现了一个新的攻击类型,compositional pattern-producing network-encoded EA (CPPN EA),在该方法中,一个不能够被人类识别是什么种类的对抗样本可以被深度神经网络以很高的置信度分成一个类。我们把这种方法分类为假正例攻击。
他们使用进化算法(EA)来生成对抗样本。为了解决使用EA算法的多分类任务,使用了multi- dimensional archive of phenotypic elites MAP-Elites(目前博主不清楚是啥)。作者首次用两种不同的方法编码图片,直接编码(灰度或HSV值)和间接编码(合成模式生成网络,CPPN)。在每次迭代过程中MAP-Elites就像普通的进化算法一样,选择一个随机的有机体,随机的变换他们,如果新的这个更健壮(有着更高的关于某类的可能性),就取代旧的那个有机体。通过这种方式,MAP-Elites可以在每个类中找到最好的个体。对许多对抗样本来说,CPPN就像JSMA一样,可以找到关键特征来改变深度神经网络的输出。同一进化过程中的许多图像在密切相关的类别上都是相似的。
8、C&W’s Attack
Carlini and Wagner为了攻击防御蒸馏(Defensive distillation)网络,提出了几种方法。他们研究发现,C&W’s Attack对大多数现存的防御方法都是有效的。
第一、他们首先定义了一个新的目标函数g,同时满足
m i n η ∣ ∣ η ∣ ∣ p + c ⋅ g ( x + η ) s . t . x + η ∈ [ 0 , 1 ] n min_\eta \ \ \ \ ||\eta||_p + c · g(x+\eta) \\ s.t. \ \ \ x + \eta \in [0,1]^n minη ∣∣η∣∣p+c⋅g(x+η)s.t. x+η∈[0,1]n
并且, 当 且 仅 当 f ( x ′ ) = l ′ 时 g ( x ′ ) ≥ 0 \ 当且仅当f(x')=l'时g(x') \ge 0 当且仅当f(x′)=l′时g(x′)≥0。用这种方式,距离和惩罚条件可以得到更好的优化。作呕这列举了7个目标函数g,通过实验凭据,有效的函数之一是:
g ( x ′ ) = m a x ( m a x i ≠ l ′ ( Z ( x ′ ) i ) − Z ( x ′ ) t , − k ) g(x') = max(max_{i\neq l'}(Z(x')_i) - Z(x')_t,-k) g(x′)=max(maxi=l′(Z(x′)i)−Z(x′)t,−k)
Z \ Z Z 表示Softmax, k \ k k 是一个常数,用来控制置信度,在论文中 k \ k k 置0。
第二,相比于使用box约束来寻找最小扰动的L-BFGS攻击方法,作者引入了一个新的变量 w \ w w 来避免box约束,其中 w 满 足 η = 1 2 ( t a n h ( w ) + 1 ) − x \ w\ 满足 \ \eta =\frac{1}{2}(tanh(w)+1) - x w 满足 η=21(tanh(w)+1)−x 。在深度学习中通用的优化器,像Adam和SGD,被用来生成对抗样本,执行了20个迭代,通过二值搜索找到最优值c。但是,他们发现,如果 ∣ ∣ η ∣ ∣ 和 g ( x + η ) \ ||\eta|| \ 和\ g(x+\eta) ∣∣η∣∣ 和 g(x+η) 的梯度不在同一范围,那么在梯度迭代搜索过程中找到一个合适的常量c是很困难的。因为这个原因,他们提出的目标函数g中的两个,就找不到优化方案。
第三,三种扰动的距离测量方法在论文中被讨论, l 0 , l 2 , l ∞ \ l_0,l_2,l_\infty l0,l2,l∞ 。作者基于距离测量方法提出了三种攻击方式, l 0 攻 击 , l 2 攻 击 , l ∞ 攻 击 \ l_0攻击,l_2攻击,l_\infty攻击 l0攻击,l2攻击,l∞攻击 。
l 2 攻 击 \ l_2 攻击 l2攻击 可以将上文中描述的目标函数描述为:
m i n w ∣ ∣ 1 2 ( t a n h ( w ) + 1 ) ∣ ∣ 2 + c ⋅ g ( 1 2 ( t a n h ( w ) + 1 ) ) min_w \ ||\frac{1}{2}(tanh(w) + 1)||_2 + c·g(\frac{1}{2}(tanh(w) + 1)) minw ∣∣21(tanh(w)+1)∣∣2+c⋅g(21(tanh(w)+1))
作者表示,蒸馏网络不能抵御 l 2 攻 击 \ l_2攻击 l2攻击
l 0 攻 击 \ l_0攻击 l0攻击 是迭代进行的,因为 l 0 \ l_0 l0 是不可微的。在每次迭代过程中,一些像素被认为是不重要的,然后被移除。像素的重要性取决于 l 2 \ l_2 l2 距离的梯度。如果剩下的像素不能够生成一个对抗样本的时候,迭代停止。
l ∞ 攻 击 \ l_\infty攻击 l∞攻击 也是一个迭代的攻击方式,在每次迭代的过程中用一个新的惩罚方式取代 l 2 \ l_2 l2 条件:
m i n c ⋅ g ( x + η ) + ∑ i [ ( η i − τ ) + ] min \ \ \ c·g(x+\eta) + \sum_i [(\eta_i - \tau)^+] min c⋅g(x+η)+i∑[(ηi−τ)+]
在每次迭代过程中, 会以0.9的因子,减少 τ \ \tau τ ,如果所有的 η i < τ \ \eta_i < \tau ηi<τ , l ∞ \ l_\infty l∞ 攻击把 τ \ \tau τ 认为 l ∞ \ l_\infty l∞ 的评估方式。
9、Zeroth Order Optimization (ZOO)
Chen等人提出了Zeroth Order Optimization (ZOO),这种攻击方法不需要梯度,所以它可以直接的部署到黑盒攻击中,而不需要模型迁移。作者修改g函数为一种像hinge loss的损失函数:
g ( x ′ ) = m a x ( m a x i ≠ l ′ ( l o g [ f ( x ) ] i ) − l o g [ f ( x ) ] l ′ , − k ) g(x') = max(max_{i\neq l'}(log[f(x)]_i) - log[f(x)]_{l'},-k) g(x′)=max(maxi=l′(log[f(x)]i)−log[f(x)]l′,−k)
并且使用对称差商估计梯度和Hessian:
∂ f ( x ) ∂ x i ≈ f ( x + h e i ) − f ( x − h e i ) 2 h ∂ 2 f ( x ) ∂ 2 x i ≈ f ( x + h e i ) − 2 f ( x ) + f ( x − h e i ) h 2 \frac{\partial f(x)}{\partial x_i} \approx \frac{f(x + he_i) − f(x − he_i)}{2h} \\ \frac{\partial ^2 f(x)}{\partial ^2 x_i}\approx \frac{f(x + he_i) − 2f(x) + f(x − he_i)}{h^2} ∂xi∂f(x)≈2hf(x+hei)−f(x−hei)∂2xi∂2f(x)≈h2f(x+hei)−2f(x)+f(x−hei)
在这里 e i \ e_i ei 表示第i个分量的标准基向量,h是一个小常数。
通过运用梯度估计和Hessian,ZOO不需要接触要被攻击的深度学习模型。但是,它需要昂贵的代价来查询和估计梯度。作者提出了ZOO-ADAM来随机的选择一个变量并且更新对抗样本。实验显示,ZOO取得了与C&W’s Attack 相当的性能。
10、Universal Perturbation
Dezfooli等人提出了一种普适性攻击方法。他们的构想是找到一个普适性的扰动向量满足:
∣ ∣ η ∣ ∣ p ≤ ϵ , P ( x ′ ≠ f ( x ) ) ≥ 1 − δ ||\eta||_p \leq \epsilon, \\ P(x' \neq f(x)) \geq 1 - \delta ∣∣η∣∣p≤ϵ,P(x′=f(x))≥1−δ
ϵ \ \epsilon ϵ 限制了普适性扰动的大小, δ \ \delta δ 控制了所有对抗样本的攻击失败率。
在每次迭代中,使用DeepFool方法为每一个输入数据获得一个最小的样本扰动,并且更新该扰动到总扰动 η \ \eta η 中去。直到大多数的样本攻击成功($\ P < 1 - \delta $),迭代才停止。实验发现,普适性扰动可以通过使用一小部分的数据集即可生成。
11、One Pixel Attack
为了避免感知测量的问题,Su等人通过仅仅修改了一个像素,生成了对抗样本。优化问题变成了:
m i n x ′ J ( f ( x ′ ) , l ′ ) s . t . ∣ ∣ η ∣ ∣ 0 ≤ ϵ 0 min_{x'} \ \ \ J(f(x'),l') \\ s.t. \ \ \ ||\eta||_0 \leq \epsilon_0 minx′ J(f(x′),l′)s.t. ∣∣η∣∣0≤ϵ0
当 ϵ 0 = 1 \ \epsilon_0 = 1 ϵ0=1 时,该方法仅仅修改了一个像素。这个新的常数也让优变得很困难。
Su等人应用了微分进化(differential evolution (DE),进化算法之一) 来找到优化解。DE不需要知道神经网络的梯度,也可以用在不可微的目标函数上。他们在CIFAR-10数据集上用三个神经网络评价了提出的方法(全卷积网络(All convolution network (AllConv)),Network in Network(NiN)和VGG16)。结果表明,70.97%的图像成功地欺骗了深层神经网络至少有一个目标类的平均置信度为97.47%。
12、Feature Adversary
Sabour等人通过最小化内部神经网络层而不是输出层的表示距离来执行了一次目标攻击。该问题可以描述为:
m i n x ′ ∣ ∣ Φ k ( x ) − Φ k ( x ′ ) ∣ ∣ s . t . ∣ ∣ x − x ′ ∣ ∣ ∞ < δ min_{x'} \ \ \ ||\varPhi_k(x) - \varPhi_k(x')|| \\ s.t. \ \ \ ||x - x'||_{\infty} < \delta minx′ ∣∣Φk(x)−Φk(x′)∣∣s.t. ∣∣x−x′∣∣∞<δ
其中, Φ k \ \Phi_k Φk 表示从图片输入到第k层输出的映射。这种方法并不是要去找到最小的扰动, δ \ \delta δ 用作扰动的约束。作者表示,一个固定的 δ \ \delta δ 值对人类的感知来说已经足够了。他们使用了L-BFGS-B来解决优化问题。对抗性图像更自然,更接近内部层的目标图像。
13、Hot/Cold
Rozsa等人提出了该方法为每个输入图片寻找多个对抗样本。他们认为只要人类感知不到,进行一些小的转换和旋转是可以的。
他们定义了一个新的标准,Psychometric Perceptual Adversarial Similarity Score (PASS),衡量与人类的明显相似性。Hot/Cold,忽略了像素上的不明显的差别,并用带有PASS的 l p \ l_p lp 距离取代(目前这个说的啥,博主也不理解,待我看完论文回来解释)。PASS包括两个步骤,首先,将修改后的图片与原图片对齐,之后,测量两个图片的的相似度。
Φ ( x ′ , x ) \ \varPhi(x',x) Φ(x′,x) 是从对抗样本到原始样本的一个单对应性的函数, H \ H H是一个单对应性的3x3的矩阵。通过最大化 x ′ 和 x \ x' 和 x x′和x 之间的enhanced correlation coefficient (ECC) 获得 H \ H H 。优化函数如下:
a r g m i n H ∣ ∣ x ‾ ∣ ∣ x ‾ ∣ ∣ − Φ ( x ′ , x ) ‾ ∣ ∣ Φ ( x ′ , x ) ‾ ∣ ∣ ∣ ∣ ⋅ ‾ 表 示 图 片 的 归 一 化 argmin_H ||\frac{\overline{x}}{||\overline{x}||} - \frac{\overline{\varPhi(x',x)}}{||\overline{\varPhi(x',x)}||}|| \\ \overline{·} 表示图片的归一化 argminH∣∣∣∣x∣∣x−∣∣Φ(x′,x)∣∣Φ(x′,x)∣∣⋅表示图片的归一化
Structural SIMilarity (SSIM)仅仅用来测量图片的显著差别度。在论中,利用SSIM,定义了一个新的测量标准,regional SSIM(RSSIM):
R S S I M ( x i , j , x i , j ′ ) = L ( x i , j , x i , j ′ ) α C ( x i , j , x i , j ′ ) β S ( x i , j , x i , j ′ ) γ α , β , γ 分 别 是 亮 度 函 数 L ( ⋅ ) , 对 比 度 函 数 C ( ⋅ ) , 结 构 函 数 S ( ⋅ ) 的 权 重 RSSIM(x_{i,j},x_{i,j}') = L(x_{i,j},x_{i,j}')^{\alpha}C(x_{i,j},x_{i,j}')^{\beta}S(x_{i,j},x_{i,j}')^{\gamma} \\ \alpha,\beta,\gamma 分别是 亮度函数L(·),对比度函数C(·),结构函数S(·)的权重 RSSIM(xi,j,xi,j′)=L(xi,j,xi,j′)αC(xi,j,xi,j′)βS(xi,j,xi,j′)γα,β,γ分别是亮度函数L(⋅),对比度函数C(⋅),结构函数S(⋅)的权重
而且,SSIM可以通过平均RSSIM的方式来计算
S S I M ( x i , j , x i , j ′ ) = 1 n ∗ m ∑ i , j R S S I M ( x i , j , x i , j ′ ) SSIM(x_{i,j},x_{i,j}') = \frac{1}{n*m}\sum_{i,j}RSSIM(x_{i,j},x_{i,j}') SSIM(xi,j,xi,j′)=n∗m1i,j∑RSSIM(xi,j,xi,j′)
PASS由对齐和相似性度量的组合定义
P A S S ( x ′ , x ) = S S I M ( Φ ∗ ( x ′ , x ) , x ) PASS(x',x) = SSIM(\varPhi^*(x',x),x) PASS(x′,x)=SSIM(Φ∗(x′,x),x)
有了新的距离后,对抗问题可以描述为:
m i n D ( x , x ′ ) s . t . f ( x ′ ) = y ′ P A S S ( x , x ′ ) ≥ γ min \ \ \ D(x,x') \\ s.t. \ \ \ f(x') = y' \\ PASS(x,x') \geq \gamma min D(x,x′)s.t. f(x′)=y′PASS(x,x′)≥γ
D ( x , x ′ ) \ D(x,x') D(x,x′)表示距离的测量函数(比如 1 − P A S S ( x , x ′ ) 或 者 ∣ ∣ x − x ′ ∣ ∣ p \ 1-PASS(x,x') 或者||x - x'||_p 1−PASS(x,x′)或者∣∣x−x′∣∣p
为了生成各种各样的对抗样本,作者定义了目标标签 l ′ \ l' l′ 为hot 类,原始标签 l \ l l 为cold类。在每次迭代中,它们都会移向目标(热)类,同时远离原始(冷)类。他们的结果表明,生成的对抗性例子与FGSM相似,并且具有更多的多样性。
14、Natural GAN
Zhao等人利用GAN作为他们方法的一部分来生成图片和文本的对抗样本,这种方法使对对抗样本对人类来说更自然。作者首先训练了一个WGAN模型,生成器G将随机噪声映射到输入域。他们还训练了一个“反相器”L将输入数据映射到密集的内部表示。因此,通过最小化内在表示距离,像Feature Adversary那样,来生成对抗性噪声。使用生成器来生成对抗样本。
m i n z ∣ ∣ z − L ( x ) ∣ ∣ s . t . f ( G ( z ) ) ≠ f ( x ) min_z \ \ \ ||z - L(x)|| \\ s.t. \ \ \ f(G(z))\neq f(x) minz ∣∣z−L(x)∣∣s.t. f(G(z))=f(x)
生成器和反相器都是用来让对抗样本变得自然的东西。Natural GAN是许多深度学习领域的通用框架。作者使用Natural GAN来进行图像分类、文本蕴含(textual entailment)和机器翻译。因为Natural GAN不需要原始神经网络的梯度,所以它也可以用到黑盒攻击中。
15、Model-based Ensembling Attack
Liu等人,在ImageNet上对深度神经网络的可迁移性进行了一项研究,然后提出了Model-based Ensembling Attack用来目标攻击。作者称,相比于无目标攻击,目标攻击在深度模型上迁移是更加困难的。使用Model-based Ensembling Attack,他们可以生成可转移的对抗样本来攻击一个黑盒模型。
作者现在大量的深度神经网络上进行白盒攻击,生成对抗样本,然后在一个黑盒模型上测试他们。Model-based Ensembling Attack通过下面的优化问题来得到
a r g m i n x ′ − l o g ( ∑ i = 1 k α i J i ( x ′ , l ′ ) ) + λ ∣ ∣ x ′ − x ∣ ∣ argmin_{x'} \ \ \ -log(\sum_{i=1}^k \alpha_i J_i(x',l'))+\lambda||x' - x|| argminx′ −log(i=1∑kαiJi(x′,l′))+λ∣∣x′−x∣∣
k \ k k是深度神经网络的个数, f i \ f_i fi是每个网络的函数, α i \ \alpha_i αi是ensemble权重( ∑ i k α i = 1 \ \sum_i^k \alpha_i = 1 ∑ikαi=1)。结果表明,Model-based Ensembling Attack 可以生成可转移性的目标对抗样本,同时增强了对抗样本对黑盒攻击的能力。 他们也证明了这个方法在生成无目标的对抗样本时,比之前的方法表现得更好。
16、Ground-Truth Attack
形式化验证技术旨在评估神经网络对zero-day 攻击的鲁棒性。Carlini等人提出了Ground-Truth攻击,该方法生成了具有最小扰动( l 1 和 l ∞ \ l_1 和l_\infty l1和l∞)的对抗样本.网络验证(Network Verificatio)总是检查对抗样本是否违反深度神经网络的属性,以及是否存在示例在一定距离内改变标签。Ground-Truth Attack执行了一个二值搜索,并且迭代的调用Reluplex来找到一个最小扰动的对抗样本。最初的对抗性例子是使用C&W’s Attack来提高性能。
Section Ⅴ 其他领域的对抗攻击示例
该节主要简要的介绍了对抗样本在强化学习、生成式网络、人脸识别、目标检测、语义分割、自然语言处理、恶意软件检测等领域的应用。
Section Ⅵ 对抗防御方法
对抗防御主要有两种方式,reactive和proactive。reactive:是在深度神经网络被构建之后检测对抗样本。proactive:在攻击者生成对抗样本前,让深度网络更鲁棒。在这一节,主要讨论了三种reactive的方法(Adversarial Detecting, Input Reconstruction, and Network Verificatio),三种proactive的方式(Network Distillation, Adversarial (Re)training, and Classifier Robustifying),以及一种emsembling method(集成方法)。
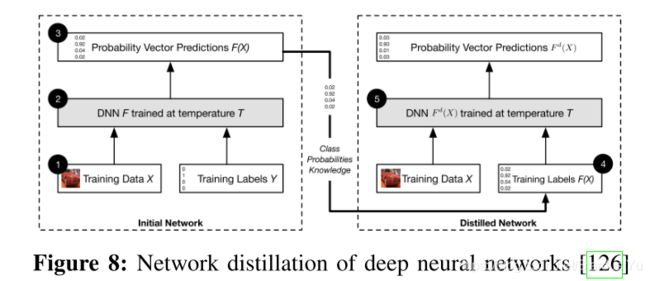
1、Network Distillation(网络蒸馏)
蒸馏网络最初是被用于减小深度网络的尺寸,通过将大网络的知识转移到小网络中。
由第一个DNN生成的类的概率被用来当作第二个DNN的输入。类的概率提取了第一个DNN学到的知识。Softmax通常是用来归一化DNN的最后一层,然后生成类的概率。第一个DNN的softmax输出是第二个DNN的输入,可以描述为:
q i = e x p ( z i / T ) ∑ j e x p ( z i / T ) q_i = \frac{exp(z_i/T)}{\sum_j exp(z_i/T)} qi=∑jexp(zi/T)exp(zi/T)
T是一个控制知识蒸馏等级的临时变量。在深度网络中,临时变量T设为1。当T变大时,Softmax的输出会变模糊。当T趋近于正无穷时,所有类的概率趋近于1/m,当T变小时,只有一个类是1,剩下的都是0。这种网络蒸馏的模式可以重复多次,可以连接多个深度网络。
在论文中,作者提到,网络蒸馏可以提取深度网络的知识,并能够提高鲁棒性。作者发现攻击主要针对网络的敏感性,接着证明了使用high-temperature softmax可以降低模型的敏感度。网络蒸馏防御在MNIST和CIFAR-10上进行了测试,降低了JSMA攻击0.5%和5%的成功率。同时,蒸馏网络也提高了神经网络的泛化能力。
2、Adversarial (Re)training(对抗训练)
带有对抗样本的训练是一个可以让神经网络更加鲁棒的一个方法。Goodfellow等人和Huang等人在训练阶段引入了对抗样本。他们在训练的每一步生成对抗样本,然后把他们加入到训练集中。对抗训练可以为神经网络提供正则化,并且提高了其准确率。
实验表明,对抗训练可以抵御单步攻击,但不能抵御迭代攻击。对抗训练只是被用来充当正则化手段来降低了过拟合。 而且,对抗训练对白盒攻击更加鲁棒。为了对付黑盒攻击,之后提出了Ensembling Adversarial Training method
3、Adversarial Detecting(对抗识别)
该方法是在测试阶段来检测对抗样本。
一些论文,训练了一个二分类网络作为检测器来辨别输入数据是合理的数据还是对抗样本。SafetyNet提取每个ReLU层输出的二值阈值作为对抗检测器的特征,并通过RBF-SVM分类器检测对抗图像。作者认为,即使对手知道检测器,他们的方法也很难被对手打败,因为对手很难找到一个最优值,无论是对对抗样本还是对SafetyNet检测器的新特征。还有一种方法是增添了一个新的类别到原始模型中,模型能够将对抗样本分类成该类。他们发现,最大平均差(MMD)和能量距离(ED)的测量可以区分是对抗样本数据集还是干净的数据集。
还有一种方法,提供了检测对抗样本的贝叶斯视野。其表示,对抗样本的不确定性比干净的数据更高。因此,他们使用一个贝叶斯神经网络来平局输入数据的不确定性来区分对抗样本和干净的数据。
同样的,还有一种方法,是使用了概率差(詹森-香农散度)作为检测器之一。另一篇论文表明,在PCA后,对抗样本在低级别组件中有着不同的系数。
PixelCNN。对抗样本的分布与干净数据的分布是不同的。他们基于PixelCNN计算了p值,然后使用p值来检测对抗样本。结果表明,该方法可以检测FGSM,BIM,DeepFool,和C&W‘s attack。
之后,有一篇论文,训练了一个具有"reverse cross-entropy"的神经网络,发现它能够更好的从干净数据中辨别出对抗样本,然后使用一种叫做Kernel density的方法检测对抗样本。“reverse cross-entropy”可以让深度网络以比较高置信度预测出正确的类,在其他类上由统一的分布。通过这种方式,深层神经网络被训练来将干净的输入映射到softmax之前的层中的低维流形。这为进一步检测对抗样本提供了极大的便利。
在强化学习领域,有一篇论文,利用了大量的先前输入的图片来预测未来的输入并检测对抗样本。
但是这些方法在损失函数稍有变化的情况下,无法抵抗C&W’s Attack
4、Input Reconstruction(输入重建)
对抗样本可以通过重建的方式变换成干净数据。在转变后,对抗样本并不会影响深度模型的预测。Gu和Rigazio提出了一种带有惩罚的自动编码器网络变体,称为深度压缩自动编码器(deep contractive autoencoder),以提高神经网络的鲁棒性。一个去噪的自动编码网络被训练用来压缩对抗样本成原始样本来消除对抗性扰动。通过两种方法来重建对抗样本,添加高斯噪声和用自动编码器压缩他们即MagNet的plan B。
PixelDefend重建对抗样本,使其回到了使用PixelCNN时的训练分布。PixelDefend改变了每一个通道的所有像素来最大化分布概率:
m a x x ′ P t ( x ′ ) s . t . ∣ ∣ x ′ − x ∣ ∣ ∞ ≤ ϵ d e f e n d max_{x'} \ \ \ P_t(x') \\ s.t. \ \ \ ||x' -x||_\infty \leq \epsilon_{defend} maxx′ Pt(x′)s.t. ∣∣x′−x∣∣∞≤ϵdefend
P t \ P_t Pt表示训练时的分布, ϵ d e f e n d \ \epsilon_{defend} ϵdefend控制对抗样本中的新的更改。PixelDefend也使用了对抗检测,为了当对抗样本没有被检测出来时,对抗样本不会有任何改变,即 ϵ d e f e n d = 0 \ \epsilon_{defend} = 0 ϵdefend=0
5、Classifier Robustifying(鲁棒的分类器)
由于对抗样本的不确定性,Bradshaw等人利用了贝叶斯分类来建立了一个更加鲁棒的神经网络。高斯变换(RBF核)也被用来提供不确定检测。提出来的神经网络叫做Gaussian Process Hybrid Deep Neural Networks (GPDNNs)。高斯变换将潜变量表示为均值和协方差函数参数化的高斯分布,并用RBF核对其进行编码。
有研究表明GPDNNs比普通的神经网络表现更好,对对抗样本更加鲁棒。作者称,GPDNNs知道他们不知道的东西。
有一篇论文观察到对抗性的例子通常是不正确类的一小部分。将类分成子类,并通过投票将所有子类的结果集合起来,以防止对抗性示例被错误分类。
6、Network Verificatio(网络验证)
验证深度网络的属性是一个对抗防御的不错的方式,因为它可以检测出新的不可见的攻击。网络验证会检查一个神经网络的属性,输入是否违反或是否满足属性。
Katz等人提出了一个使用ReLU激活函数的验证方法,叫做Reluplex。他们使用Satisfiability Modulo Theory (SMT 可满足性模理论)来验证神经网络,即,在一个小扰动下,没有现有的对抗样本可以让神经网络进行错误分类。他们也证明了网络验证问题是一个NP难问题。Carlini等人提出的$\ max(x,y) = ReLU(x-y) + y $和 $ ||x|| = ReLU(2x) - x$拓展了ReLU函数的假设。但是Reluplex由于巨大的计算量,运行的十分慢,只能针对那些由几百个节点的神经网络。之后,提出了两种解决方法,一、按重要性排序那些要检查的节点,而、共享验证信息。
Gopinath等人放弃了单独检查每个节点的方法,提出了了DeepSafe,使用Reluplex提供深层神经网络的安全区域。他们还引入了目标鲁棒性(targeted robustness),一个只针对目标类的安全域。
7、Ensembling Defenses(集成防御)
由于对抗样本的多样性,因此可以使用多种防御策略一起运行来进行防御。
之前提及的PixelDefend时由一个对抗样本检测器和一个输入重建器组合成的防御策略。
MagNet包含一个或多个检测器以及一个重建器,分别为Plan A和Plan B。检测器用来找到离分类边界比较远的对抗样本。在一篇论文中,测量了在输入和编码输入的距离,以及(输入和编码输入的)softmax输出概率散度。对抗样本具有大的距离和概率散度。为了解决距离边界比较近的对抗样本,MagNet使用了一个基于自动编码器的重建器,重建器会将对抗样本映射到合理的样本。
8、对抗防御总结
基本上所有的防御策略都只对部分攻击策略有效,甚至对一些比较强的、不可见的攻击毫无办法。而且目前大多数的对抗防御是针对CV中的对抗样本。
Section Ⅶ 挑战与讨论
在这一节,我们主要来讨论目前(及论文发布时,2017年)在对抗样本领域的挑战以及潜在的问题。尽管近年来许多方法和理论被提出,但是大量的基本的问题需要一个很好的解释,许多挑战需要被解决。对攻击者和防御者来说,对抗样本的存在的原因是一个有趣的和最基本的问题。在这一节主要讨论一下几个问题
- 为什么对抗样本会有迁移性
- 如何阻止对抗样本的迁移性
- 为什么一些对抗防御方法有效还其他的无效
- 如何去测量一个攻击和防御的健壮性
- 如何去评价一个深度网络对抗可见与不可见的对抗样本的鲁棒性
A、迁移性
迁移性是对抗样本的基本属性。Szegedy等人首次发现,生成的对抗样本可以欺骗在不同数据集上训练的神经网络。Papernot等人发现,生成的对抗样本可以欺骗不同结构的神经网络。迁移性对黑盒攻击是极其重要的。当攻击者想要攻击受害模型时,他可以先训练一个替代的神经网络,然后为替代的神经网络生成对抗样本,那么,由于迁移性,受害模型将容易受到这些对抗性例子的攻击。从防御者视角来看,如果我们组织了对抗样本的迁移性,那么我们就可以抵御所有的需要接近模型和要求迁移性的白盒攻击者。
我们从易到难的三个层次定义了对抗样本的迁移性,一、不同数据训练的同一神经网络结构间的迁移;二、为同一任务训练的不同神经网络结构间的迁移;三、为不同任务训练的神经网络的迁移
Papernot等人研究了在机器学习与深度学习网络之间的迁移性。他们发现,对抗样本可以在不同的参数、机器学习模型的训练数据集之间进行,甚至可以跨不同的机器学习技术进行。
Liu等人观察了在复杂模型和大数据集上的目标攻击和无目标攻击的迁移性。他们发现,无目标攻击的对抗样本更具有迁移性。他们观察到,不同模型的决策边界彼此吻合得很好。因此,他们提出了Model-Based Ensembling Attack,以创建可迁移的目标攻击的对抗样本。
Tramèr等人。发现到模型决策边界的距离平均大于同一方向上两个模型边界之间的距离。这可以解释对抗样本的迁移性存在的原因。Tramèr等人,通过一个反例,声称迁移性可不能并不是深度网络的内在属性
B、对抗样本的存在性
对抗样本存在的原因仍然是一个悬而未决的问题。对抗样本是深层神经网络的固有特性吗?对抗样本是高性能深层神经网络的““Achilles’ heel”吗?已经提出了许多假说来解释存在性。
**一、数据不完整。**一个假设是,对抗样本是测试数据集中的角落案例,具有低概率性和低覆盖性。通过训练一个PixelCNN,发现对抗性例子的分布不同于干净的数据。即使对于简单的高斯模型,鲁棒的模型也可能比“标准”模型更复杂,需要更多的训练数据。
二、模型容量。对抗样本不仅仅是深度网络的一种现象,而且是所有分类器的一种现象。有篇论文表明对抗样本是模型在高维流行(high dimensional manifolds)中太线性的结果。还有一篇论文结果表明,在线性情况下,当决策边界接近训练数据的流形时,存在对抗实例。当然,也有不同的意见,有篇论文认为,对抗样本是因为分类器对特定任务的低灵活性,线性并不是一个合理的解释。还有论文表示,是因为稀疏不连续性导致分类器不稳定而产生的对抗样本。
三、没有鲁棒的模型。有论文表示深层神经网络的决策边界本质上是不正确的,不能检测出语义对象。另有论文表明,如果数据集是由一个具有较大潜在空间的光滑生成模型生成的,则对对抗样本来说没有鲁棒的分类器。同样的,还有一篇论文证明如果一个模型是有一个球状的数据集训练出来的,而且该模型误分类了数据集中的一小部分,那么就会存在具有小的扰动的对抗样本。
除了用于图像分类的对抗样本之外任务,如第五节所述,在各种应用中产生了对抗样本。他们中的许多人采用了完全不同的方法。一些应用程序可以使用与图像分类任务相同的方法。然而,有些人需要提出一种新的方法。目前对对抗样本的研究主要集中在图像分类任务上。现有的论文没有解释不同应用之间的关系,以及存在一种适用于所有应用的通用攻击/防御方法。
C、鲁棒性评估
攻防对抗就是一场军备竞赛一样,一种被提出用来防止现有攻击的防御方法后来被证明容易受到一些新攻击的攻击,反之亦然。一些防御措施表明他们可以防御一次特定的攻击,但后来由于攻击的轻微变化而失败。因此,一个深度网络的鲁棒性评估是很有必要的。例如,有篇论文为线性分类器和二分类器提供了鲁棒性的上界。深部神经网络的鲁棒性评估需要进一步的探索。
一、一种评价深层神经网络鲁棒性的方法。许多深层神经网络计划部署在安全关键环境中。仅防御现有攻击是不够的。Zero-day攻击(新的攻击方法)对深层神经网络的危害更大。需要一种评估深层神经网络鲁棒性的方法,特别是对于Zero-day攻击,这有助于人们理解模型预测的可信度以及在现实世界中我们可以依赖它们的程度。有篇论文对评估进行了初步研究。此外,这个问题不仅在于深层神经网络模型的性能,还在于其保密性和保密性。
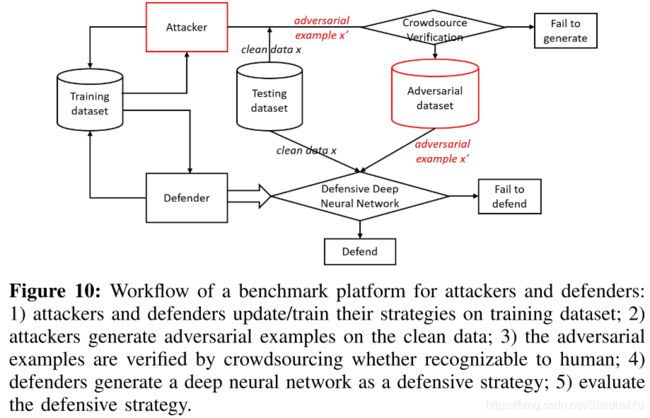
二、一个攻击和防御的基准平台。 大多数攻击和防御在没有公开代码的情况下描述了它们的方法,也没有说方法中使用的参数。这给其他研究人员复制他们的解决方案并提供相应的攻击/防御带来了困难。例如,Carlini尽力“找到最好的防守参数+随机初始化”。一些研究人员甚至因为实验环境的不同而得出了不同的结论。如果存在任何基准,即敌方和防御者以统一的方式进行实验(例如,相同的威胁模型、数据集、分类器、攻击/防御方法),则可以对不同的攻击和防御技术进行更精确的比较。 Cleverhans[144]和Foolbox[145]是开放源码的库,用于基准测试深层神经网络在对抗图像方面的脆弱性。他们建立了评估攻击的框架。然而,这两种工具都缺少防御策略。提供由不同方法生成的对抗实例数据集,将有助于发现深层神经网络的盲点,开发新的防御策略。这个问题也出现在深度学习的其他领域。 Google Brain在NIPS 2017竞赛赛道上组织了三场比赛,包括目标对抗攻击、无目标对抗攻击和对抗防御。比赛中的数据集由一组以前从未使用过的图像组成,这些图像由人工标记,1000个图像用于开发,5000个图像用于最终测试。提交的攻击和比赛被用作自我评估的基准。对手的攻击和防御是按欺骗防御的次数/正确分类图像来评分的。 我们提出了workflow这个平台来进行攻击和防御。
三、稳健性评估的各种应用。类似于各种应用的对抗实例的存在,广泛的应用使得很难评估深度神经网络体系结构的鲁棒性。如何比较不同威胁模型下生成对抗样本的方法?我们是否有一个通用的方法来评估所有场景下的健壮性?解决这些未解决的问题是未来的一个方向。
Section Ⅷ 总结
本文综述了近年来深部神经网络中对抗样本的发现。我们研究了现有的生成对抗实例的方法。提出了对抗性例子的分类。探讨了对抗实例的应用及对策。本文试图涵盖深度学习领域中对抗性例子的最新研究。与最近关于对抗性例子的研究相比,我们分析了和讨论了现在面临的挑战和潜在的问题。