机器学习——线性回归
线性回归
- 线性回归定义
- 一般线性算法
-
- 学习参数
- 代码实现
- Ridge Regression 岭回归
-
- Ridge介绍
- 代码实现
- Lasso回归
-
- 学习参数
- 代码实现
- 参考
线性回归定义
线性回归(Liner Regession,LR),简单的来说就将输入空间的变量映射到输出空间的一种模型。LR形式简单,易于实现,具有较好的解释性,一般用于连续性变量的回归问题,如:预测身高,房价等。同时,LR也是一种判别学习模型。
一般线性算法
按照机器学习的一般套路:寻找假设函数,写出损失函数,使损失函数最小。假设训练样本集如下:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\} D={ (x1,y1),(x2,y2),...,(xm,ym)}
其中, x i x_i xi表示第i个样本,共有m个样本, x i j x_{ij} xij表示第i个样本第j个位置的值, x i ∈ R d x_i \in R^d xi∈Rd。
假设函数:
h θ ( x i ) = θ 0 + θ 1 x i 1 + θ 2 x i 2 + . . . + θ d x i d h_{\theta}(x_i)= \theta_0+\theta_1x_{i1}+\theta_2x_{i2}+...+\theta_dx_{id} hθ(xi)=θ0+θ1xi1+θ2xi2+...+θdxid
θ = ( θ 0 , θ 1 , θ 2 , . . . θ d ) T \theta=(\theta_0,\theta_1,\theta_2,...\theta_d)^T θ=(θ0,θ1,θ2,...θd)T是需要学习的参数,令每个样本的 x 0 = 1 x_0=1 x0=1,可以写成下面的向量化形式:
h θ ( x i ) = θ T x i h_\theta(x_i)=\theta^Tx_i hθ(xi)=θTxi
损失函数:
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 = 1 2 ( X θ − Y ) T ( X θ − Y ) J(\theta)=\frac12\sum_{i=1}^m(h_\theta(x_i)-y_i)^2=\frac12(X\theta-Y)^T(X\theta-Y) J(θ)=21i=1∑m(hθ(xi)−yi)2=21(Xθ−Y)T(Xθ−Y)
目标:
θ = arg min θ = J ( θ ) \theta=\arg\min_{\theta} = J(\theta) θ=argθmin=J(θ)
学习参数
要使损失函数最小,我们可以使用著名的梯度下降法,对 J ( θ ) J(\theta) J(θ)求偏导数。
∂ J ( θ ) ∂ θ j = ∂ 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 ∂ θ j = 1 2 ∑ i = 1 m 2 ∗ ( h θ ( x i ) − y i ) ∂ h θ ( x i ) ∂ θ j = 1 2 ∑ i = 1 m 2 ∗ ( h θ ( x i ) − y i ) ∂ θ T x i ∂ θ j = 1 2 ∑ i = 1 m 2 ∗ ( h θ ( x i ) − y i ) ∂ ( θ 0 + θ 1 x i 1 + θ 2 x i 2 + . . . + θ d x i d ) ∂ θ j = ∑ i = 1 m ( h θ ( x i ) − y i ) x i j \frac{\partial J(\theta)}{\partial \theta_j}=\frac{\partial \frac12\sum_{i=1}^m(h_\theta(x_i)-y_i)^2}{\partial \theta_j} = \frac12\sum_{i=1}^m2*(h_\theta(x_i)-y_i) \frac{\partial h_\theta(x_i)}{\partial \theta_j} \\= \frac12\sum_{i=1}^m2*(h_\theta(x_i)-y_i) \frac{\partial \theta^Tx_i}{\partial \theta_j} \qquad \qquad \qquad \qquad \qquad \qquad \\ = \frac12\sum_{i=1}^m2*(h_\theta(x_i)-y_i) \frac{\partial (\theta_0+\theta_1x_{i1}+\theta_2x_{i2}+...+\theta_dx_{id})}{\partial \theta_j} \\=\sum_{i=1}^m(h_\theta(x_i)-y_i)x_{ij}\qquad \qquad \qquad\qquad \qquad \qquad \quad \quad \qquad ∂θj∂J(θ)=∂θj∂21∑i=1m(hθ(xi)−yi)2=21i=1∑m2∗(hθ(xi)−yi)∂θj∂hθ(xi)=21i=1∑m2∗(hθ(xi)−yi)∂θj∂θTxi=21i=1∑m2∗(hθ(xi)−yi)∂θj∂(θ0+θ1xi1+θ2xi2+...+θdxid)=i=1∑m(hθ(xi)−yi)xij
所以对 θ j \theta_j θj的更新可以表示为如下:
θ j = θ j − α ∗ ∑ i = 1 m ( h θ ( x i ) − y i ) x i j \theta_j=\theta_j-\alpha * \sum_{i=1}^m(h_\theta(x_i)-y_i)x_{ij} θj=θj−α∗i=1∑m(hθ(xi)−yi)xij
其中,参数更新一次使用所有的样本叫批量梯度下降,更新一次参数使用一个样本叫随机梯度下降。批量梯度下降相对随机梯度下降来说有更快的收敛速度,基本能达到全局最优点,但是如果样本过多,更新一次所用时间较长。而随机梯度下降更新一次参数所用的时间比较短,可能会收敛到局部最优。
对损失函数矢量化求导,令导数等于零可得到参数的解析解,过程如下:
∂ J ( θ ) ∂ θ = ∂ 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 ∂ θ = ∂ 1 2 ( X θ − Y ) T ( X θ − Y ) ∂ θ = ∂ ( θ T X T X θ − θ T X T Y − Y T X θ + Y T Y ) ∂ θ \frac{\partial J(\theta)}{\partial \theta}=\frac{\partial \frac12\sum_{i=1}^m(h_\theta(x_i)-y_i)^2}{\partial \theta}=\frac{\partial \frac12(X\theta-Y)^T(X\theta-Y)}{\partial \theta} \\ =\frac{\partial (\theta^TX^TX\theta-\theta^TX^TY-Y^TX\theta+Y^TY)}{\partial \theta} \quad ∂θ∂J(θ)=∂θ∂21∑i=1m(hθ(xi)−yi)2=∂θ∂21(Xθ−Y)T(Xθ−Y)=∂θ∂(θTXTXθ−θTXTY−YTXθ+YTY)
下面分别对每一项求导:
∂ θ T X T X θ ∂ θ = 2 X T X θ \frac{\partial \theta^TX^TX\theta}{\partial \theta}=2X^TX\theta ∂θ∂θTXTXθ=2XTXθ
∂ θ T X T Y ∂ θ = ∂ Y T X θ ∂ θ = X T Y \frac{\partial \theta^TX^TY}{\partial \theta}=\frac{\partial Y^TX\theta}{\partial \theta}=X^TY ∂θ∂θTXTY=∂θ∂YTXθ=XTY
∂ Y T Y ∂ θ = 0 → \frac{\partial Y^TY}{\partial \theta}=\overrightarrow{0} ∂θ∂YTY=0
综上有:
∂ J ( θ ) ∂ θ = X T X θ − X T Y \frac{\partial J(\theta)}{\partial \theta}=X^TX\theta-X^TY ∂θ∂J(θ)=XTXθ−XTY
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J(\theta)}{\partial \theta}=0 ∂θ∂J(θ)=0,可解得 θ = ( X T X ) − 1 X T Y \theta=(X^TX)^{-1}X^TY θ=(XTX)−1XTY,值得注意的是一定要 X T X X^TX XTX可逆才能有上述解析解。
代码实现
# 线性回归批量梯度下降算法
def bathGradientDescent(dataX, dataY, alpha, iternum=10000):
samplesNumbers, SampleFeatureNumbers = np.shape(dataX)
weights_cur = np.zeros((SampleFeatureNumbers, 1))
for i in range(iternum):
weights_cur += alpha * dataX.T @ (dataY - dataX @ weights_cur) / samplesNumbers
return weights_cur
#线性回归随机梯度下降算法
def stochasticGradientDescent(dataX, dataY, alpha, iternum=10000):
samplesNumbers, SampleFeatureNumbers = np.shape(dataX)
weights_cur = np.zeros((SampleFeatureNumbers, 1))
for i in range(iternum):
for j in range(samplesNumbers):
weights_cur += alpha * dataX[j:j+1].T * (dataY[j]-dataX[j:j+1] @ weights_cur)
if i % 500 == 0:
print("error: ", 0.5 * (dataX @ weights_cur - dataY).T @ (dataX @ weights_cur - dataY))
return weights_cur
实验结果
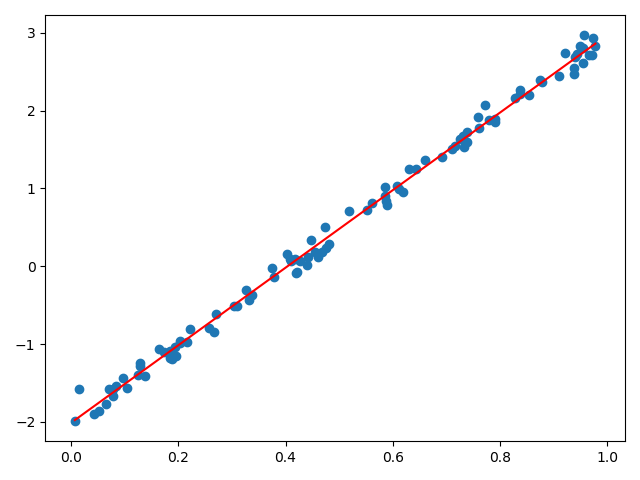
根据实验结果,在进行线性回归之前最好先对样本数据做预处理,如:归一化,标准化,正则化等,否则有可能得不到实验结果。
Ridge Regression 岭回归
Ridge介绍
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法。另一方面, X T X X^TX XTX不可逆时,岭回归方法,非常巧妙的化解了这个死胡同,即在 X T X X^TX XTX的基础上加上一个较小的lambda扰动 ,从而使得行列式不再为0。Ridge回归通常也称为Ridge回归,它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项,和Lasso回归的区别是Ridge回归的正则化项是L2范数,而Lasso回归的正则化项是L1范数。线性回归是经验风险最小化,岭回归是结构风险最小化,具体Ridge回归的损失函数表达式如下:
损失函数:
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 + 1 2 λ ∣ ∣ θ ∣ ∣ 2 2 = 1 2 ( X θ − Y ) T ( X θ − Y ) + 1 2 λ θ T θ J(\theta)=\frac12\sum_{i=1}^m(h_\theta(x_i)-y_i)^2+\frac12 \lambda ||\theta||_2^2=\frac12(X\theta-Y)^T(X\theta-Y)+\frac12 \lambda \theta^T \theta J(θ)=21i=1∑m(hθ(xi)−yi)2+21λ∣∣θ∣∣22=21(Xθ−Y)T(Xθ−Y)+21λθTθ
根据一般线性回归的参数学习容易得到下面的结果:
θ j = θ j − α ∗ ∑ i = 1 m ( h θ ( x i ) − y i ) x i j + λ θ j \theta_j=\theta_j-\alpha * \sum_{i=1}^m(h_\theta(x_i)-y_i)x_{ij}+ \lambda \theta_j θj=θj−α∗i=1∑m(hθ(xi)−yi)xij+λθj
∂ J ( θ ) ∂ θ = X T X θ − X T Y + λ θ \frac{\partial J(\theta)}{\partial \theta}=X^TX\theta-X^TY+\lambda \theta ∂θ∂J(θ)=XTXθ−XTY+λθ
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J(\theta)}{\partial \theta}=0 ∂θ∂J(θ)=0,可解得 θ = ( X T X + λ I ) − 1 X T Y \theta=(X^TX+\lambda I)^{-1}X^TY θ=(XTX+λI)−1XTY。上述正规方程与一般线性回归的正规方程相比,多了一项 λ I \lambda I λI,其中 I I I表示单位矩阵。假如 X T X X^TX XTX是一个奇异矩阵(不满秩),添加这一项后可以保证该项可逆。由于单位矩阵的形状是对角线上为1其他地方都为0,看起来像一条山岭,因此而得名。
代码实现
X1 = np.random.random([100, 1])
X2 = np.c_[np.ones([100, 1]), X1]
Y1 = 5 * X1 - 2 + np.random.randn(100, 1)*0.1
weights = np.linalg.inv(X2.T @ X2 + 0.01 * np.identity(2)) @ X2.T @ Y1
实验结果
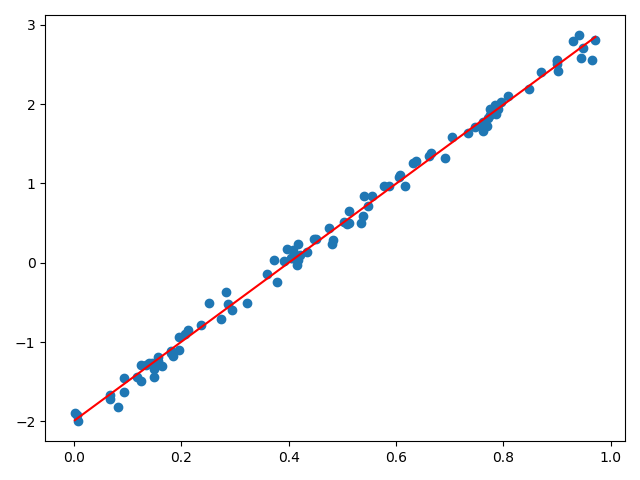
实验结果分析,对于如何选取 λ \lambda λ的值是岭回归的核心问题,如果只是为了使 X T X X^TX XTX可逆,则 λ \lambda λ可选取小一点,具体如何选择 λ \lambda λ的值,有兴趣的可以参考此文章 。
Lasso回归
Lasso与岭回归比较相似,岭回归使用的是L2范数作为正则项(也称惩罚项),而Lasso回归使用的是L1范数。岭回归无法剔除变量,而Lasso回归模型,将惩罚项由L2范数变为L1范数,可以将一些不重要的回归系数缩减为0,达到剔除变量的目的。关于L1、L2简单的解释就是:
L1:L1正则化最大的特点是能稀疏矩阵,进行庞大特征数量下的特征选择
L2:L2正则能够有效的防止模型过拟合,解决非满秩下求逆困难的问题
损失函数:
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 + λ ∣ ∣ θ ∣ ∣ 1 J(\theta)=\frac12\sum_{i=1}^m(h_\theta(x_i)-y_i)^2+ \lambda ||\theta||_1 J(θ)=21i=1∑m(hθ(xi)−yi)2+λ∣∣θ∣∣1
学习参数
使Lasso的代价函数最小,可以使用坐标下降法或梯度下降算法,只不过这里的L1范数是不可导的,故在对L1范数计算梯度时使用次导数。
梯度下降
∂ ∣ ∣ θ ∣ ∣ 1 ∂ θ j = { λ , θ j > 0 [ − λ , λ ] , θ j = 0 − λ , θ j < 0 \frac{\partial ||\theta||_1}{\partial \theta_j}= \begin{cases} \lambda,\quad \quad \quad \quad \quad \theta_j>0 \\ [-\lambda,\lambda], \quad \qquad \theta_j=0 \\ - \lambda, \qquad \qquad \quad \theta_j<0 \end{cases} ∂θj∂∣∣θ∣∣1=⎩⎪⎨⎪⎧λ,θj>0[−λ,λ],θj=0−λ,θj<0
令 n j = ∑ i = 1 m x i j 2 n_j= \sum_{i=1}^mx_{ij}^2 nj=∑i=1mxij2, m j = ∑ i = 1 m ( ∑ k = 1 , k ≠ j d θ k x i k − y i ) x i j m_j=\sum_{i=1}^m(\sum_{k=1,k\neq j}^d \theta_kx_{ik}-y_i)x_{ij} mj=∑i=1m(∑k=1,k̸=jdθkxik−yi)xij,方程 ∂ J ( θ ) ∂ θ j + ∂ ∣ ∣ θ ∣ ∣ 1 ∂ θ j = 0 \frac{\partial J(\theta)}{\partial \theta_j}+\frac{\partial ||\theta||_1}{\partial \theta_j}=0 ∂θj∂J(θ)+∂θj∂∣∣θ∣∣1=0的解分为下面三种情况:
∂ J ( θ ) ∂ θ j + ∂ ∣ ∣ θ ∣ ∣ 1 ∂ θ j = ∑ i = 1 m ( h θ ( x i ) − y i ) x i j + λ ~ = ∑ i = 1 m ( ∑ k = 1 , k ≠ j d θ k x i k − y i ) x i j + θ j ∑ i = 1 m x i j 2 + λ ~ = ∑ i = 1 m ( ∑ k = 1 , k ≠ j d θ k x i k − y i ) x i j + θ j n j + λ ~ = m j + θ j n j + λ ~ = 0 \frac{\partial J(\theta)}{\partial \theta_j}+\frac{\partial ||\theta||_1}{\partial \theta_j}=\sum_{i=1}^m(h_{\theta}(x_i)-y_i)x_{ij}+\tilde \lambda \\ =\sum_{i=1}^m(\sum_{k=1,k\neq j}^d \theta_kx_{ik}-y_i)x_{ij}+\theta_j \sum_{i=1}^mx_{ij}^2 +\tilde\lambda \\ = \sum_{i=1}^m(\sum_{k=1,k\neq j}^d \theta_kx_{ik}-y_i)x_{ij}+\theta_j n_j+\tilde\lambda \qquad \\ = m_j+\theta_jn_j+\tilde\lambda=0 \qquad\qquad\qquad\qquad \qquad ∂θj∂J(θ)+∂θj∂∣∣θ∣∣1=i=1∑m(hθ(xi)−yi)xij+λ~=i=1∑m(k=1,k̸=j∑dθkxik−yi)xij+θji=1∑mxij2+λ~=i=1∑m(k=1,k̸=j∑dθkxik−yi)xij+θjnj+λ~=mj+θjnj+λ~=0
- θ j > 0 , λ ~ = λ \theta_j>0,\tilde\lambda=\lambda θj>0,λ~=λ
θ j = − m j − λ n j , m j < − λ \theta_j=\frac{-m_j-\lambda}{n_j} ,\qquad m_j<-\lambda θj=nj−mj−λ,mj<−λ - θ j = 0 , λ ~ ∈ [ − λ , λ ] \theta_j=0,\tilde\lambda\in[-\lambda,\lambda] θj=0,λ~∈[−λ,λ]
θ j = 0 , m j = − λ ~ , 即 m j ∈ [ − λ , λ ] \theta_j=0 ,\qquad m_j=-\tilde\lambda,即m_j\in[-\lambda,\lambda] θj=0,mj=−λ~,即mj∈[−λ,λ] - θ j < 0 , λ ~ = − λ \theta_j<0,\tilde\lambda=-\lambda θj<0,λ~=−λ
θ j = λ − m j n j , m j > λ \theta_j=\frac{\lambda-m_j}{n_j} ,\qquad m_j>\lambda θj=njλ−mj,mj>λ
综上:
θ j = { ( − m j − λ ) / n j , m j < − λ 0 , m j ∈ [ − λ , λ ] ( λ − m j ) / n j , m j > λ \theta_j= \begin{cases} (-m_j-\lambda)/n_j,\quad \quad \quad m_j<-\lambda \\0, \quad \qquad \qquad \qquad \qquad m_j \in[-\lambda,\lambda] \\ (\lambda-m_j)/n_j, \quad \quad \qquad m_j>\lambda \end{cases} θj=⎩⎪⎨⎪⎧(−mj−λ)/nj,mj<−λ0,mj∈[−λ,λ](λ−mj)/nj,mj>λ
代码实现
# 线性回归 Lasso回归,lambda的选择可以使用交叉验证法
def lassoLinerRegession(X, Y, lmbd, iternum=1000):
samplesNumbers, sampleFeatureNumbers = np.shape(X)
weights_cur = np.ones((sampleFeatureNumbers, 1))
nk = np.sum(X ** 2, axis=0).reshape(-1, 1)
for i in range(iternum):
for j in range(sampleFeatureNumbers):
mj = X[:, j:j + 1].T @ (X @ weights_cur - Y) - weights_cur[j] * nk[j]
if mj < -lmbd:
weights_cur[j] = (-mj - lmbd) / (nk[j] + 1.0)
elif mj > lmbd:
weights_cur[j] = (lmbd - mj) / (nk[j] + 1.0)
else:
weights_cur[j] = 0
return weights_cur
参考
【1】正则化的线性回归 —— 岭回归与Lasso回归
【2】Latex各种命令、符号、公式、数学符号、排版等
【3】机器学习中正则化项L1和L2的直观理解
【4】岭回归、LASSO回归(包括公式推导)
【5】次梯度(subgradient)方法