- 前言
- 树的定义
- 树的存储结构
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
- 二叉树
- 定义
- 特点
- 形态
- 特殊二叉树
- 斜树
- 满二叉树
- 完全二叉树
- 二叉树的性质
- 二叉树的存储结构
- 二叉树的顺序存储结构
- 二叉树的链式存储结构
- 二叉树的遍历
- 遍历原理
- 遍历方法
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 二叉树的建立
- 树、森林和二叉树的转换
- 树转换为二叉树
- 森林转换为二叉树
- 二叉树转换为树
- 二叉树转换为森林
- 树和森林的遍历
- 树的遍历
- 森林的遍历
前言
主要描述二叉树。
李柱明博客:https://www.cnblogs.com/lizhuming/p/15487394.html
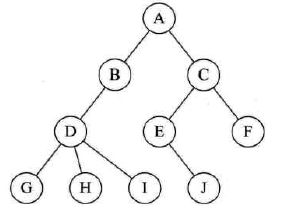
树的定义
树:
- 树是 n(n>=0) 个结点的有限集。
- n = 0 时为空树。
- n > 0 时,即是非空树时,有且仅有一个根结点。
- m > 0 时,子树的个数没有限制,但它们一定互不相交。
结点:
-
结点的度:结点拥有的子树数。
-
叶结点或终结点:度为 0 的结点。
-
非终结点或分支结点:度不为 0 的结点。
-
内部结点:除根结点外,分支结点也称为内部结点。
-
树的度:树内各结点的度的最大值。
结点关系:
- 孩子(child):结点的子树的根称为该结点的孩子。
- 双亲(parent):该结点称为孩子的双亲(父母同体,唯一的一个)。
- 兄弟(sibling):同一个双亲的孩子之间互称兄弟。
- 祖先:结点的祖先是从根到该结点所经分支上的所有结点。
- 子孙:以某结点为根的子树中的任一结点都称为该节点的子孙。
树的其它相关概念:
- 层次(level):从根开始定义起,根为第一层,根的孩子为第二层。
- 堂兄弟:双亲在同一层的结点互为堂兄弟。
- 深度(depth)或高度:树中结点的最大层次称为树的深度或高度。
- 有序树/无序树:如果将树中结点的各子树看成从左至右有次序的,不能互换的,则称该树为有序树,否则为无序树。
- 森林(forest):m(m>=0)棵互不相交的树的集合。
树的存储结构
简单的顺序存储结构无法直接反映逻辑关系,不能满足树的实现要求。
故充分利用顺序存储和链式存储结构的特点,介绍三种不同的表示法:
- 双亲表示法。
- 孩子表示法。
- 孩子兄弟表示法。
双亲表示法
引入:除根节点外,其余每个结点,不一定有孩子,但一定有且仅有一个双亲
定义:设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。
- data:数据域,存储结点的数据信息。
- parent:指针域,存储该结点的双亲在数组中的下标。
- 约定:根节点的位置域为-1。
缺点:
- 找一个结点的孩子需要遍历树。
上述第一个缺点引发的思考:
-
需要关注什么数据域就在数据结构中添加什么数据域。如双亲域、长子域、兄弟域等等。
- 如需要关注结点的孩子,则添加结点的长子域。
参考代码:
/* 树的双亲表示法结点数据结构 */
#define MAX_TREE_SIZE 100
typedef int tree_elem_type;
/* 结点结构 */
typedef struct tree_node
{
int parent; // 双亲位置
// int firstchild; // 长子位置
// int rightsib; // 右兄弟位置
tree_elem_type data; // 数据
}tree_node_t;
/* 树结构 */
typedef struct tree
{
int root; // 根节点位置
int num; // 当前节点数
tree_node_t nodes[MAX_TREE_SIZE];
}tree_t;
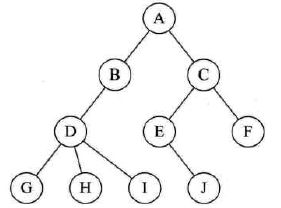
孩子表示法
多重链表表示法:
- 每个结点有多个指针域,其中每个指针指向一棵子树的根节点,这种方法叫做多重链表表示法。
方案 1:
- 设置指针域的个数为树的度。
- 即是结点数据结构的内容为:data 和 n(树的度)个孩子域。

- 特点:可能存在空间浪费。
方案 2:
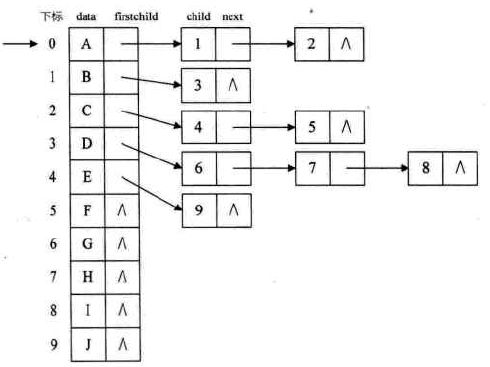
孩子表示法:
-
把每个结点的孩子结点排列起来,以单链表作存储结构,则 n 个结点有 n 个孩子链表,如果是叶子结点,则此单链表为空。然后 n 个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。
-
孩子表示法的两种结点数据结构:
-
缺点:找双亲需要遍历树。
- 解决:表头数组的表头结点数据结构添加双亲域。
参考代码:
/* 树的孩子表示法结点数据结构 */
#define MAX_TREE_SIZE 100
typedef int tree_elem_type;
/* 孩子结点结构 */
typedef struct c_tree_node
{
int child; // 孩子下标
struct c_tree_node *next; // 下一个
}c_tree_node_t;
/* 表头结构 */
typedef struct tree_top
{
c_tree_node_t *firstchild; // 头结点
tree_elem_type data; // 数据
}tree_top_t;
/* 树结构 */
typedef struct tree
{
int root; // 根节点位置
int num; // 当前节点数
tree_top_t nodes[MAX_TREE_SIZE];
}tree_t;
孩子兄弟表示法
引入:
- 任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。
- 所以可以设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
参考代码:
/* 树的孩子兄弟表示法结点数据结构 */
typedef int tree_elem_type;
typedef struct tree_node
{
struct tree_node *firstchild; // 长子域
struct tree_node *rightsib; // 右兄域
tree_elem_type data; // 数据
}tree_node_t;
二叉树
定义
二叉树的定义:
- 二叉树是 n(n>=0) 个结点的有限集合,该集合或为空集,或由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
- 是有序树。
特点
二叉树特点:
- 二叉树中不存在大于 2 的结点。
- 左子树和右子树是有序树。
- 只有一颗子树也要区分左右子树。
形态
二叉树的五种基本形态:
- 空二叉树。
- 只有一个根结点。
- 根结点只有左子树。
- 根结点只有右子树。
- 根结点有左、右子树。
特殊二叉树
斜树
左斜树&右斜树:
- 左斜树:
满二叉树
满二叉树:
-
定义:所有分支结点都存在左右子树,并且所有叶子都在同一层。
-
特点:
- 叶子只能出现在最下一层。
- 非叶子结点的度一定是 2。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
完全二叉树
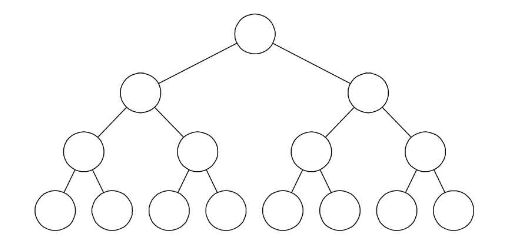
完全二叉树:
-
定义:对一棵具有 n 个结点的二叉树按层序编号,如果编号 i(1<=i<=n)的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同,则此二叉树为完全二叉树。
-
特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左边连续位置。
- 倒数第二层若有叶子结点,一定都在右边连续位置。
- 若结点的度为 1,则该结点只有左孩子。即是不存在只有右子树的情况。
- 同样结点数的二叉树,完全二叉树的深度最小。
-
判断方法:给每个结点按满二叉树的结构逐层排序,如果编号出现空档,就不是,否则就是。
二叉树的性质
性质 1:在二叉树的第 i 层上至多有 2i-1 个结点(i>=1)。
性质 2:深度为 k 的二叉树至多有 2k-1 个结点(k>=1)。
性质 3:对任何一棵二叉树 T,如果其终端结点数为 n0,度为 2 的结点数为 n2,则 n0 = n2+1。
性质 4:具有 n 个结点的完全二叉树的深度为[log2n ] + 1([X]表示不大于 X 的最大整数)。
性质 5:如果对一颗有 n 个结点的完全二叉树(其深度为[log2n ] + 1)的结点按层序编号(从第 1 层到第[log2n ] + 1 层,每层从左到右),对任一结点 i(1<=i<=n)有:
- 如果 i=1,则结点 i 是二叉树的根,无双亲。
- 如果 i>1,则其双亲是结点[i/2]。
- 如果 2i>n,则结点 i 无左孩子(结点 i 为叶子结点);否则其左孩子是结点 i。
- 如果 2i+1>n,则结点 i 无右孩子;否则其右孩子是结点 2i+1。
二叉树的存储结构
有顺序存储结构和链式存储结构。
二叉树的顺序存储结构
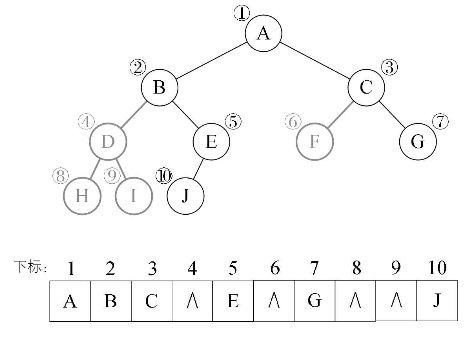
二叉树的顺序存储结构:
- 存储方法:按完全二叉树编号,编号就是下标。
- 缺点:当树不为完全二叉树时存在空间浪费。
二叉树的链式存储结构
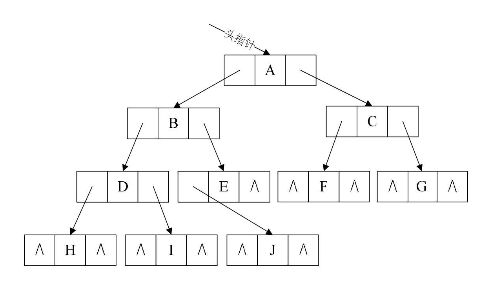
二叉树的链式存储结构:
二叉树的遍历
遍历是二叉树中非常重要的操作。
遍历原理
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点都被访问 1 次。
遍历方法
四种遍历方法:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
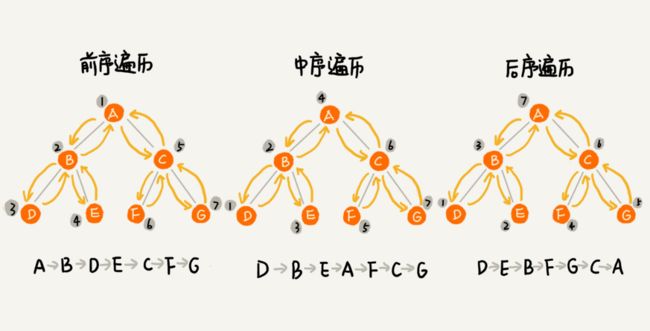
前、中、后序表示的是节点与它的左右子树节点遍历打印的先后顺序。
前序遍历
前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
代码实现思路:
-
中-> 左 -> 右。使用栈辅助实现。
- 方法 1:使用递归思想。(相当于使用系统栈)
- 方法 2:非递归,采用自实现的栈辅助。
参考代码(递归):
/* 顺序存储结构 */
void pre_order_traverse(bi_tree tree,int e)
{
visit(tree[e]); // 打印父节点
if(tree[2*e+1]!=nil) /* 左子树不空 */
pre_traverse(tree,2*e+1); // 递归
if(tree[2*e+2]!=nil) /* 右子树不空 */
pre_traverse(tree,2*e+2); // 递归
}
/* 链式存储结构 */
void pre_order_traverse(bi_tree *tree)
{
if(tree==NULL)
return;
printf("%c",tree->data);/* 显示结点数据,可以更改为其它对结点操作 */
pre_order_traverse(tree->lchild); /* 再先序遍历左子树 */
pre_order_traverse(tree->rchild); /* 最后先序遍历右子树 */
}
中序遍历
中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树
代码实现思路:
-
左-> 中 -> 右。使用栈辅助实现。
- 方法一:使用递归思想。
- 方法 2:非递归,采用自实现的栈辅助。
参考代码(递归):
/* 顺序存储结构 */
void in_order_traverse(bi_tree tree,int e)
{
if(tree[2*e+1]!=nil) /* 左子树不空 */
in_traverse(tree,2*e+1); // 递归
visit(tree[e]); // 打印父节点
if(tree[2*e+2]!=nil) /* 右子树不空 */
in_traverse(tree,2*e+2); // 递归
}
/* 链式存储结构 */
void in_order_traverse(bi_tree *tree)
{
if(tree==NULL)
return;
in_order_traverse(tree->lchild); /* 再先序遍历左子树 */
printf("%c",tree->data);/* 显示结点数据,可以更改为其它对结点操作 */
in_order_traverse(tree->rchild); /* 最后先序遍历右子树 */
}
后序遍历
后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
代码实现思路:
-
左-> 右 -> 中。
- 使用递归思想。
- 方法 2:非递归,采用自实现的栈辅助。
参考代码(递归):
/* 顺序存储结构 */
void post_order_traverse(bi_tree tree,int e)
{
if(tree[2*e+1]!=nil) /* 左子树不空 */
post_traverse(tree,2*e+1); // 递归
if(tree[2*e+2]!=nil) /* 右子树不空 */
post_traverse(tree,2*e+2); // 递归
visit(tree[e]); // 打印父节点
}
/* 链式存储结构 */
void post_order_traverse(bi_tree *tree)
{
if(tree==NULL)
return;
post_order_traverse(tree->lchild); /* 再先序遍历左子树 */
post_order_traverse(tree->rchild); /* 最后先序遍历右子树 */
printf("%c",tree->data);/* 显示结点数据,可以更改为其它对结点操作 */
}
层序遍历
根起,从上而下,从左至右。
对于顺序存储,只需要按下标顺序输出即可。
但是对于链式存储结构就复杂点,思路如下:借助队列的方式实现:
- 先把跟节点入队。
- 获取队头并打印,然后把当前队头节点的左右孩子入队。
- 重复步骤 2。
/* 顺序存储结构:直接打印数组 */
void level_order_traverse(bi_tree tree)
{
int i=MAX_TREE_SIZE-1;
int j=0;
while(tree[i]==nil)
i--; /* 找到最后一个非空结点的序号 */
for(j=0;j<=i;j++) /* 从根结点起,按层序遍历二叉树 */
if(tree[j]!=nil)
visit(tree[j]); /* 只遍历非空的结点 */
printf("\n");
}
/* 链式存储结构:借助队列 */
void level_order_traverse(bi_tree_node* tree)
{
bi_tree_node* temp = NULL;
queue_push(tree); // 跟节点入队
while (!queue_empty())
{
temp = queue_pop();
printf("%d ", temp->data); //输出队首结点
if (temp->left) //把Pop掉的结点的左子结点加入队列
queue_push(temp->left);
if (temp->right) // 把Pop掉的结点的右子结点加入队列
queue_push(temp->right);
}
}
二叉树的建立
二叉树的扩展二叉树:
- 为了能让每个结点确认是否有左右孩子,将每个结点的空指针引出一个虚结点,其值为一特定值,比如"#"
- 这种处理后的二叉树为原二叉树的扩展二叉树。
- 扩展二叉树就可以做到一个遍历序列确定一棵二叉树。
树、森林和二叉树的转换
树转换为二叉树
二叉树除了根节点,其余节点最多有三条线:
- 与双亲。(注意:在该节点上没有双亲域)
- 做孩子。
- 右孩子。
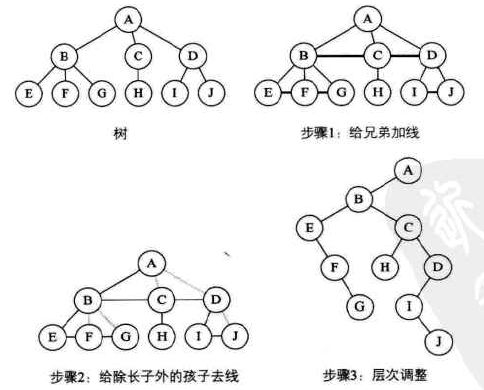
树转换为二叉树的步骤:
-
加线:所有兄弟结点之间加一条线。
-
去线:对树中每个结点,只保留与第一个孩子的线。删除与其它孩子的线。
-
层次调整:
- 第一个孩子是二叉树的左孩子。
- 右兄弟是右孩子。
森林转换为二叉树
森林转换为二叉树的步骤:
- 把每棵树都转换为二叉树。
- 从第二棵树起,将其根节点插入到前一棵树的根节点作为其右孩子。
二叉树转换为树
二叉树转为树的步骤:
- 加线:当前节点与左孩子的右孩子、左孩子的右孩子的右孩子、左孩子的右孩子的右孩子的右孩子......连线。
- 去线:去掉原二叉树中所有节点与其右孩子的连线。
- 层次调整。
二叉树转换为森林
二叉树的根节点有右孩子,则说明该二叉树可以就可以转换为森林。
二叉树转换为森林的步骤:
- 去线:从根节点其,取出根节点与右孩子的线,得出的右孩子树,也去除与右孩子的线,循环下去直至右孩子树没有右孩子为止。
- 将每棵二叉树转换为树。
树和森林的遍历
树的遍历
树的遍历有两种:
- 先序遍历:先访问根再依次访问子。
- 后序遍历:先访问依次访问子,再访问根。
森林的遍历
森林的遍历也有两种:
- 先序遍历:一棵树先序遍历完再下一棵树。
- 后序遍历:一棵树后序遍历完再下一棵树。