Python实现聚类 KMeans算法

#-*- coding: utf-8 -*-
'''
# author： 影子
# datetime： 2021-05-18 12:10 
# ide： PyCharm
target : 完成一个简单的KMeans聚类算法
'''
from numpy import *

# 欧式距离函数
def Euclidean_Distance(vecA,vecB):
    return sqrt(sum(power(vecA-vecB,2)))

# 随机设置k个质心
def Rand_Cent(DataSet,k):
    n = shape(DataSet)[1]     # 获取数据集的维度
    centroids = mat(zeros([k,n]))  # 初始化一个k行n列的二维数组，数组初始值全部为0，然后用mat函数将其转化为矩阵
    for j in range(n):
        minj = min(DataSet[:,j])
        rangej = float(max(DataSet[:,j])-minj)
        centroids[:,j] = mat(minj+rangej*random.rand(k,1)) # 随机生成一个范围在[min_j,max_j]的数据
    return centroids   # 返回k个初始质心

# k-Means算法实现
def kMeans(DataSet,k,Dist=Euclidean_Distance,set_cent=Rand_Cent):
    '''
    :param DataSet: 需要聚类的数据集
    :param k: 聚类数目
    :param Dist: 距离函数,此处调用了欧式距离函数
    :param set_cent: 初始质心函数，此处调用随机生成的质心函数
    :return: 质心点；数据对应的聚类簇
    '''
    m = shape(DataSet)[0]   # 获取样本个数
    centoids = set_cent(DataSet,k)  # 初始化质心
    clusterAssment = mat(zeros((m,2))) # 第一列存放每个样本的聚类簇，第二列存放对该样本到该聚类中心的距离
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):   # 遍历所有样本
            minDist = inf # 初始设定最小距离为无穷大
            minIdex = -1 # 初始设定样本聚类簇为 -1
            for j in range(k): # 对每个样本，计算到其他k个聚类中心的距离
                DistJI = Dist(centoids[j,:],DataSet[i,:])
                if minDist > DistJI:  # 该样本到最小距离的聚类中心记录下来,此样本记录为该簇
                    minDist = DistJI
                    minIdex = j
            if clusterAssment[i,0] != minIdex: # 判断样本所属簇是否更新，若更新则记为True
                clusterChanged = True
            clusterAssment[i,:]=minIdex,minDist # 将样本的聚类簇和到该聚类簇中心的距离记录下来
        for cent_i in range(k):
            cluster = DataSet[nonzero(clusterAssment[:,0].A==cent_i)[0]]
            '''
            clusterAssment[:,0]：记录每个样本的聚类簇
            clusterAssment[:,0].A：将其转化为行矩阵
            nonzero(clusterAssment[:,0].A==cent_i)[0]：获得元素为Ture的样本下标
            整句含义：获得数据集中聚类簇为cent_i的样本
            '''
            centoids[cent_i,:] = mean(cluster,axis=0) # 按行取均值
    return centoids,clusterAssment # 返回质心点；每个样本的(聚类簇+最短距离)

# 画图
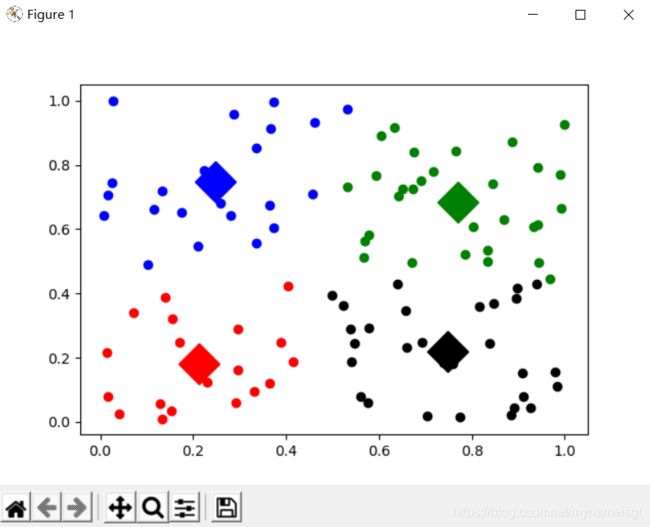
def show(DataSet,k,centroids,clusterAssment):
    from matplotlib import pyplot as plt
    m,n = DataSet.shape
    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr'] # 样本集的样式
    for i in range(m):
        markIdex = int(clusterAssment[i,0])
        plt.plot(DataSet[i,0],DataSet[i,1],mark[markIdex])
    mark= ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb'] # 质点的样式
    for i in range(k):
        plt.plot(centroids[i,0],centroids[i,1],mark[i],markersize=20)
    plt.show()


def main():
    DataSet = random.rand(100,2) # 随机生成100行2列的数据
    DataSet = mat(DataSet) # 转化为矩阵
    k=4 # 设置聚类簇
    myCentroids,clustAssing = kMeans(DataSet,k) # 调用kMeans算法
    print('聚类的质心为')
    print(myCentroids)
    show(DataSet,k,myCentroids,clustAssing)  # 画图

if __name__ == '__main__':
    main()