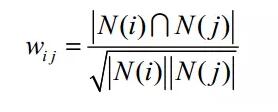推荐系统-基于物品的协同过滤推荐算法完整实现(从原始数据到推荐物品-C#版)
由于最近在用C#写一个项目,项目的关键部分就是需要用到推荐算法,以前基本没有去了解过推荐算法,看了很多资料,了解到目前基于物品的协同过滤推荐算法是最符合我的项目的。所以就动手从数据库的连接取原始数据到最终的推荐实现了这个算法,在具体实现过程中碰到了很多坎坷,在此记录下我用C#实现这个算法整个过程的思路和具体实现代码,其他语言大致相同,将代稍加改动就可。
推荐算法相关介绍(来源于网络资料)
1.基于用户的协同过滤算法(UserCF)
该算法利用用户之间的相似性来推荐用户感兴趣的信息,个人通过合作的机制给予信息相当程度的回应(如评分)并记录下来以达到过滤的目的进而帮助别人筛选信息,回应不一定局限于特别感兴趣的,特别不感兴趣信息的纪录也相当重要。但有很难解决的两个问题,一个是稀疏性,即在系统使用初期由于系统资源还未获得足够多的评价,很难利用这些评价来发现相似的用户。另一个是可扩展性,随着系统用户和资源的增多,系统的性能会越来越差。
2.基于物品的协同过滤算法(ItemCF)
内容过滤根据信息资源与用户兴趣的相似性来推荐商品,通过计算用户兴趣模型和商品特征向量之间的向量相似性,主动将相似度高的商品发送给该模型的客户。由于每个客户都独立操作,拥有独立的特征向量,不需要考虑别的用户的兴趣,不存在评价级别多少的问题,能推荐新的项目或者是冷门的项目。这些优点使得基于内容过滤的推荐系统不受冷启动和稀疏问题的影响。
基于物品的推荐算法流程
1.构建用户–>物品的倒排;
2.构建物品与物品的同现矩阵;
3.计算物品之间的相似度,即计算相似矩阵;
4.根据用户的记录,给用户推荐物品;
具体实现步骤:
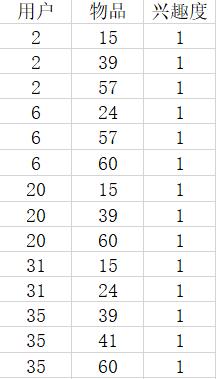
基础数据实例,这个数据是从测试数据库拿出来的数据,用户列为用户ID,物品列是物品ID,兴趣度暂时都设为1:
1.构建用户–>物品的倒排矩阵:
用户->物品倒排矩阵主要是用来标识用户对某个物品是否有相应的记录(例如喜欢或购买过)
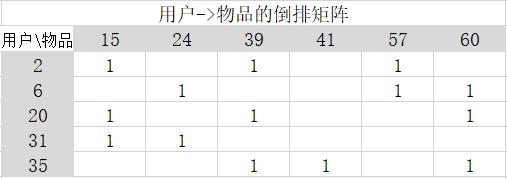
根据基础数据构建的用户–>物品的倒排矩阵矩阵应如下:
解释:行表示用户,列表示物品 ,1则表示有此记录,如坐标[0,4]表示第一行的第五列,也就是ID为2的用户购买或喜欢过ID为57的物品。
所以现在我们需要把基础数据构建成这么一个用户–>物品的倒排矩阵。
就是构建这个矩阵,我开始一直没想通到底该怎么去把原始数据构建成这个矩阵。其实我们一步一步来分析。
- 构建思路
- 需要用户ID列表(并且是按照升序或者降序进行排序,这样可以方便查找以及获取)
- 需要物品ID列表(升序或降序排序)
- 用户ID所对应的物品ID记录
- 创建一个倒排矩阵的二维数组,因为倒排矩阵行表示user,列表示good,因此这个二维数组的就是int[usersCount,goodsCount]
- 循环得到从数据库中取得的数据的每一行中的user值和good值,说明用户user购买过此good
- 在经过升序排序的List
users 和List goods中查找user和good值的索引a,b - 将二维数组的[a,b]值置为1,表示对应的user是否购买过或喜欢过此good,循环完毕后即可得到用户->物品的倒排矩阵二维数组
实际代码如下,
//连接数据库操作和计算代码片段运行时间
GlobalFunAndVar global = new GlobalFunAndVar();
//物品列表(ID)
List users;
//用户列表(ID)
List goods;
//物品的总用户数
int[] goodUsersNum;
//存放数据库取得的数据
DataTable dataTable;
//用户的总数量
int usersCount = 0;
//物品的总数量
int goodsCount = 0;
///
/// 转化数据库中的数据
///
public void init()
{
//统计代码片段运行时间开始
global.stopwatchBegin();
dataTable = global.SqlDataAdapDS("select [user],good from recommendTest group by [user],good").Tables[0];
//统计代码片段运行时间结束
global.stopwatchEnd();
int dataTableRowCount = dataTable.Rows.Count;
SortedSet setUser = new SortedSet();
SortedSet setGood = new SortedSet();
for (int i = 0; i < dataTableRowCount; i++)
{
setUser.Add((int)dataTable.Rows[i][0]);
setGood.Add((int)dataTable.Rows[i][1]);
}
users = setUser.ToList();
goods = setGood.ToList();
usersCount = users.Count;
goodsCount = goods.Count;
}
//用户->物品的倒排矩阵二维数组
int[,] users_Goods_Matrix;
///
/// 用户->物品的倒排矩阵二维数组
///
/// (users_Goods_Matrix);
return users_Goods_Matrix;
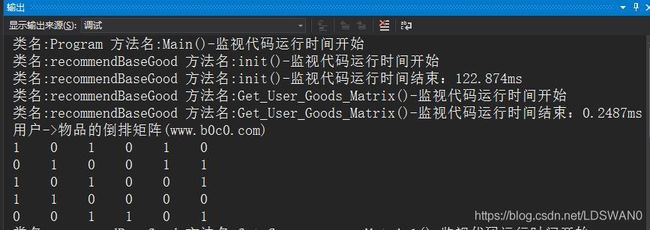
} 运行结果:
哈,现在已经正确构建出用户->物品的倒排矩阵二维数组了,接下来就是去构建物品与物品的同现矩阵二维数组。
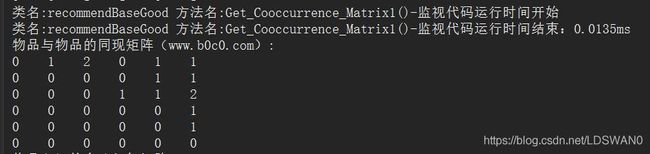
2.构建物品与物品的同现矩阵:
同现矩阵是物品-物品的矩阵,表示同时购买过或喜欢过矩阵点[x,y](x,y分别表示一个物品)对应的两个物品的用户数,是根据用户物品倒排表计算出来的。
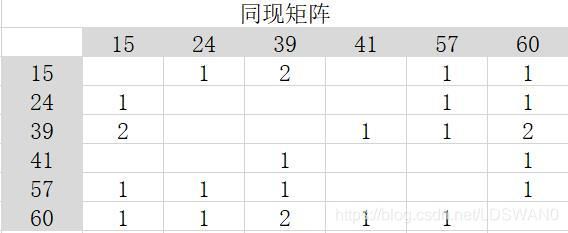
如根据上面的用户物品倒排矩阵可以计算出如下的共现矩阵:
构建思路:
- 创建一个物品与物品同现矩阵的二维数组,行和列都表示good,所以此矩阵是一个方阵,因此这个二维数组就是int[goodsCount,goodsCount]
- 循环倒排矩阵的二维数组每一行
- 循环倒排矩阵的二维数组每一行中的每一列
- 比如现在开始循环,从[0,0]坐标开始,则就把[0,0]的值与[0,1]、[0,2]、[0,3]、[0,4]、[0,5]的值进行逐个判断。
- 如果两个的值都为1,则说明此用户购买过或喜欢过这两个good的记录、现在就该将同现矩阵中的对应坐标值加1
- 那么这个对应坐标[x,y]是多少呢,x应该是此时循环倒排矩阵中列的值,y应该是对比坐标的y。
- 比如现在循环到[0,2],[0,2]与[0,4]的值都为1,则同现矩阵的对应坐标[2,4]值就加1。
- 同现矩阵的对角线值是必定相等的,所以同现矩阵的对应坐标[4,2]值也应该加1(但是在实际使用中没有什么意义,只用到对角线一边的值,而且经我测试20万数据量,只赋值对角线一边,我经过了多次测试,测试结果就是代码效率将提高三分之一)
实际代码如下:
//物品与物品的同现矩阵二维数组
int[,] Cooccurrence_Matrix;
//物品的总用户数
int[] goodUsersNum;
//用户购买过或喜欢过对应的物品 key为users中的下标,value所有物品字符串,中间用,隔开
Dictionary likeGoods = new Dictionary();
//用户没有购买过或喜欢过对应的物品 key为users中的下标,value所有物品字符串,中间用,隔开
Dictionary recommendGoods = new Dictionary();
public int[,] Get_Cooccurrence_Matrix1()
{
int i, j, k, y, CompareCount;
//物品与物品的同现矩阵二维数组
Get_User_Goods_Matrix();
global.stopwatchBegin();
//同现矩阵
Cooccurrence_Matrix = new int[goodsCount, goodsCount];
//存储物品的总用户数
goodUsersNum = new int[goodsCount];
for (i = 0; i < usersCount; i++)
{
string userLikeGoodsStr = "";
string recommendGoodsStr = "";
for (j = 0; j < goodsCount; j++)
{
/* 判断起始对比值是否为1,
* 如果为0的话说明user_Goods_Matrix[i, j]的值与第i行中的任何一个数据一定是对比不成功的则直接跳过。
*/
if (users_Goods_Matrix[i, j] == 1)
{
userLikeGoodsStr = userLikeGoodsStr + j + ",";
goodUsersNum[j] = goodUsersNum[j] + 1;
//统计物品总用户数结束
//实际对比次数=CompareCount-1
CompareCount = goodsCount - j;
for (k = 1; k < CompareCount; k++)
{
y = j + k;
if (users_Goods_Matrix[i, y] == 1)
{
Cooccurrence_Matrix[j, y]++;
//Cooccurrence_Matrix[y, j]++; 放弃对角线值
}
}
}
else
recommendGoodsStr = recommendGoodsStr + j + ",";
}
likeGoods.Add(i, userLikeGoodsStr);
recommendGoods.Add(i, recommendGoodsStr);
}
global.stopwatchEnd();
Console.WriteLine("物品与物品的同现矩阵(www.b0c0.com):");
OutPutArray(Cooccurrence_Matrix);
return Cooccurrence_Matrix;
} 运行结果:
构建出物品与物品的同现矩阵后,接下来就是去构建物品之间的余弦相似矩阵了。
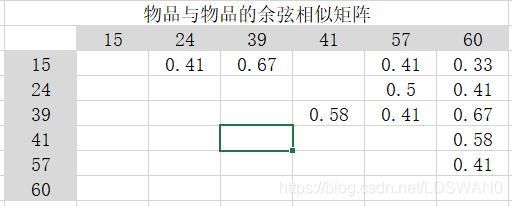
3.构建物品与物品的余弦相似矩阵:
计算物品之间的相似度,即计算相似矩阵,两个物品之间的相似度公式如下图所示。
其中分子含义为:N(i)表示喜欢物品i的用户数,N(j)表示喜欢物品j的用户数,|N(i)⋂N(j)|表示同时喜欢物品i,j的用户数。
所以物品与物品的同现矩阵其实就是此式的分子。
分母含义为:N(i)表示喜欢物品i的用户数*N(j)表示喜欢物品j的用户数,然后开平方。
物品的总用户数已经在构建出物品与物品的同现矩阵方法中求出.
所以构建物品之间的余弦相似矩阵二维数组只需要循环物品与物品的同现矩阵对角线一边的每一个值然后再套公式即可。
实际代码如下:
//物品之间的余弦相似矩阵二维数组
double[,] Cosine_Similar_Matrix;
///
/// 构建物品之间的余弦相似矩阵二维数组
///
/// (Cosine_Similar_Matrix);
return Cosine_Similar_Matrix;
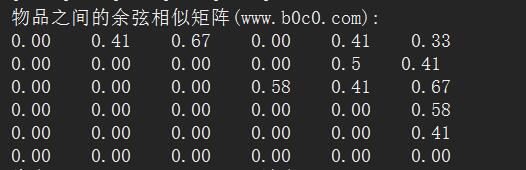
} 运行结果:
下一步就是计算预测兴趣度,也就是推荐物品了。
4.计算预测兴趣度(推荐物品):
最终推荐的是什么物品,是由预测兴趣度决定的。
公式:物品j预测兴趣度=用户喜欢的物品i的兴趣度×物品i和物品j的相似度
这个用户喜欢的物品i的兴趣度我在这里只是测试 都默认为1,实际上这个兴趣度可以是对该物品的评分、或者是对该物品的购买次数,或者访问次数等实际情况来决定的。在我的项目里可以是对该物品的购买次数和评分混合选项综合来作为兴趣度。
所以计算预测兴趣度需要:
//用户购买过或喜欢过对应的物品
Dictionary
//用户没有购买过或喜欢过对应的物品
Dictionary
比如:
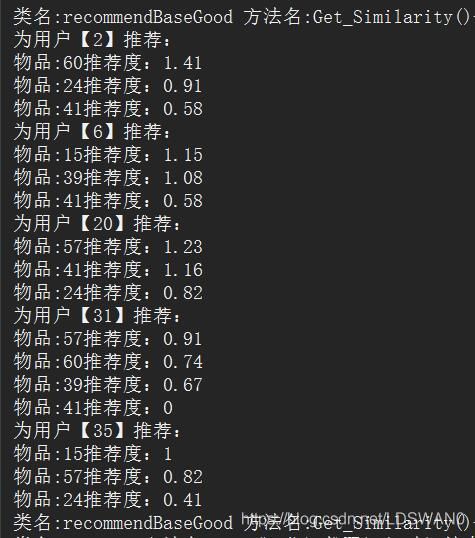
比如2用户购买过15、39、57三个物品,兴趣度分别为1、1、1
2用户的预测物品(24、41、60)的兴趣度就为:
24物品:1×0.41+1×0.5=0.91
41物品:1×0.58=0.58
60物品:1×0.33+1×0.67+1×0.41=1.41
其实就是可以把购买过的物品(15、39、57)看成余弦相似矩阵二维数组x坐标,预测物品(24、41、60)看成余弦相似矩阵二维数组y坐标。以此来求出所有物品的预测相似度。
实际代码如下:
///
/// 计算预测兴趣度
///
/// tes = new Dictionary();
likeGoods.TryGetValue(b, out likeGoodsStr);
recommendGoods.TryGetValue(b, out recommendGoodsStr);
if (!string.IsNullOrEmpty(recommendGoodsStr))
{
int[] m = Array.ConvertAll(recommendGoodsStr.Substring(0, recommendGoodsStr.Length - 1).Split(','), int.Parse);
if (!string.IsNullOrEmpty(likeGoodsStr))
{
int[] n = Array.ConvertAll(likeGoodsStr.Substring(0, likeGoodsStr.Length - 1).Split(','), int.Parse);
for (int i = 0; i < m.Count(); i++)
{
int x = m[i];
double goodSimilarity = 0.00;
for (int j = 0; j < n.Count(); j++)
{
int y = n[j];
if (x < y)
goodSimilarity += Cosine_Similar_Matrix[x, y];
else
goodSimilarity += Cosine_Similar_Matrix[y, x];
}
tes.Add(m[i], goodSimilarity);
}
}
}
tes = tes.OrderByDescending(p => p.Value).ToDictionary(o => o.Key, p => p.Value);
string va = "";
Console.WriteLine("为用户【"+users[b]+"】推荐:");
foreach (KeyValuePair k in tes)
{
Console.WriteLine("物品:" + goods[k.Key] + "推荐度:" + k.Value);
top10++;
}
}
global.stopwatchEnd();
} 运行结果:
至此整个基于物品的协同过滤推荐算法就结束了。注意我的算法实现是把所有的用户推荐都计算了,在实际应用中,我们只计算指定用户的推荐就行。
可以对代码改动为这样:
public int[,] Get_Cooccurrence_Matrix(int userSub)
{
int i, j, k, y, CompareCount;
//物品与物品的同现矩阵二维数组
Get_User_Goods_Matrix();
global.stopwatchBegin();
//同现矩阵
Cooccurrence_Matrix = new int[goodsCount, goodsCount];
//存储物品的总用户数
goodUsersNum = new int[goodsCount];
for (i = 0; i < usersCount; i++)
{
string userLikeGoodsStr = "";
string recommendGoodsStr = "";
for (j = 0; j < goodsCount; j++)
{
/* 判断起始对比值是否为1,
* 如果为0的话说明user_Goods_Matrix[i, j]的值与第i行中的任何一个数据一定是对比不成功的则直接跳过。
*/
if (users_Goods_Matrix[i, j] == 1)
{
if (userSub == i)
userLikeGoodsStr = userLikeGoodsStr + j + ",";
goodUsersNum[j] = goodUsersNum[j] + 1;
//统计物品总用户数结束
//实际对比次数=CompareCount-1
CompareCount = goodsCount - j;
for (k = 1; k < CompareCount; k++)
{
y = j + k;
if (users_Goods_Matrix[i, y] == 1)
{
Cooccurrence_Matrix[j, y]++;
//Cooccurrence_Matrix[y, j]++; 放弃对角线值
}
}
}
else
if (userSub == i)
recommendGoodsStr = recommendGoodsStr + j + ",";
}
if (userSub == i)
{
likeGoods.Add(i, userLikeGoodsStr);
recommendGoods.Add(i, recommendGoodsStr);
}
}
global.stopwatchEnd();
Console.WriteLine("物品与物品的同现矩阵(www.b0c0.com):");
OutPutArray(Cooccurrence_Matrix);
return Cooccurrence_Matrix;
}
public double[,] Get_Cosine_Similar_Matrix(int userSub)
{
Get_Cooccurrence_Matrix(userSub);
Cosine_Similar_Matrix = new double[goodsCount, goodsCount];
int i = 0, j = 0;
for (i = 0; i < goodsCount; i++)
{
if (i <= j)
for (j = 0; j < goodsCount; j++)
{
if (Cooccurrence_Matrix[i, j] != 0)
{
double a = Math.Round((Cooccurrence_Matrix[i, j] / Math.Sqrt(goodUsersNum[i] * goodUsersNum[j])), 2);
Cosine_Similar_Matrix[i, j] = a;
}
}
}
Console.WriteLine("物品之间的余弦相似矩阵(www.b0c0.com):");
OutPutArray(Cosine_Similar_Matrix);
return Cosine_Similar_Matrix;
}
public void Get_Similarity(int user)
{
Get_Cosine_Similar_Matrix(users.IndexOf(user));
global.stopwatchBegin();
string likeGoodsStr = "";
string recommendGoodsStr = "";
//存储为用户推荐的物品集合,key为推荐物品Id,value推荐度
Dictionary tes = new Dictionary();
likeGoods.TryGetValue(users.IndexOf(user), out likeGoodsStr);
recommendGoods.TryGetValue(users.IndexOf(user), out recommendGoodsStr);
if (!string.IsNullOrEmpty(recommendGoodsStr))
{
int[] m = Array.ConvertAll(recommendGoodsStr.Substring(0, recommendGoodsStr.Length - 1).Split(','), int.Parse);
if (!string.IsNullOrEmpty(likeGoodsStr))
{
int[] n = Array.ConvertAll(likeGoodsStr.Substring(0, likeGoodsStr.Length - 1).Split(','), int.Parse);
for (int i = 0; i < m.Count(); i++)
{
int x = m[i];
double goodSimilarity = 0.00;
for (int j = 0; j < n.Count(); j++)
{
int y = n[j];
if (x < y)
goodSimilarity += Cosine_Similar_Matrix[x, y];
else
goodSimilarity += Cosine_Similar_Matrix[y, x];
}
tes.Add(m[i], goodSimilarity);
}
}
}
tes = tes.OrderByDescending(p => p.Value).ToDictionary(o => o.Key, p => p.Value);
string va = "";
int top10 = 0;
Console.WriteLine("为用户【" + user + "】推荐:");
foreach (KeyValuePair k in tes)
{
if (top10 != 10)
{
//goodsName.TryGetValue(goods[k.Key], out va);
Console.WriteLine("物品:" + goods[k.Key] + "推荐度:" + k.Value);
top10++;
}
else
break;
}
global.stopwatchEnd();
} 调用Get_Similarity的时候只需传入用户的ID即可,就能得到此用户的Top10推荐物品。
下面我在我笔记本上测试了一下效率
这个算法效率基本上影响较大的因素就是物品的数据量,而物品在我的项目里预测基本在1000左右。
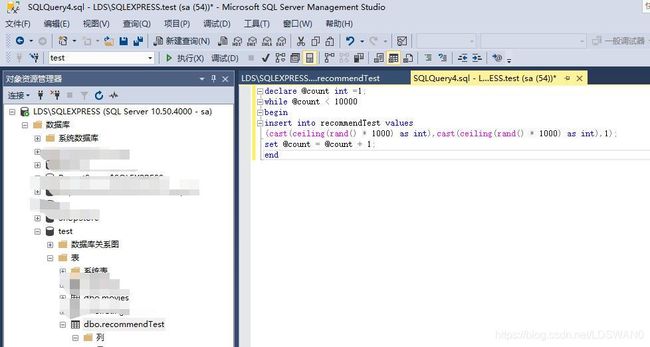
1、往数据库随生成成1万条购买记录(数据可重复,代表多次购买),用户Id范围在1-1000之内,物品Id范围在1-1000之内,基本可理解为1千用户量、1千物品量。
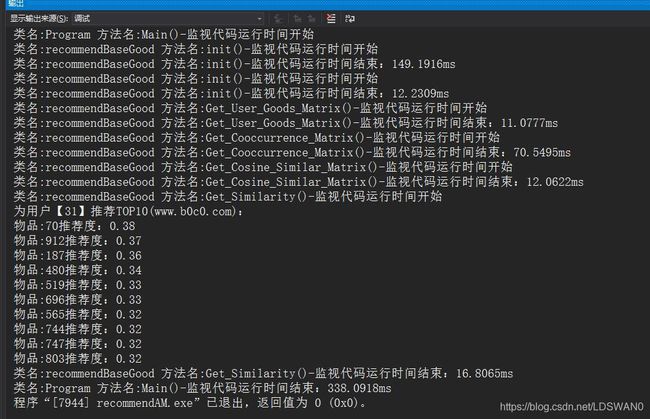
我在init方法中放了两个测试时间,因为init中有连接数据库的操作,所以我测试了连接数据库的时间和其他片段的时间。
在这个数据量下性能还是可以的,可以看到连接数据库操作其实就占了一半的时间,总运行时间大概在320毫秒,去除数据库的操作以及输出,程序运行实际时间大概在150毫秒。
2、往数据库随生成成10万条购买记录(数据可重复,代表多次购买),用户Id范围在1-1000之内,物品Id范围在1-1000之内,基本可理解为1千用户量、1千物品量。
经过多次运行测试、在这个数据量下总运行时间大概在1100±100毫秒,去除数据库的操作以及输出, 程序运行实际时间大概在650±100毫秒。
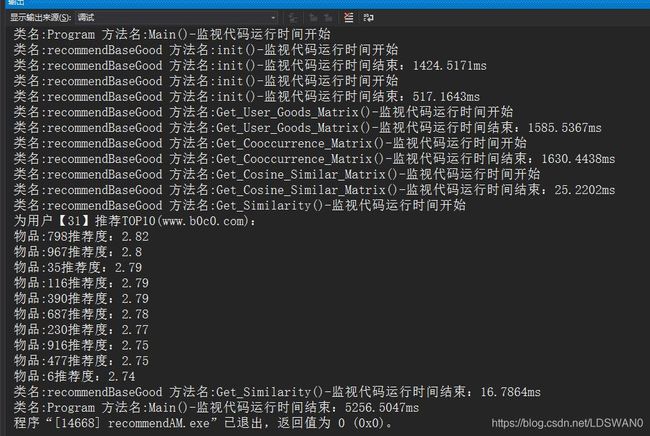
3、往数据库随生成成50万条购买记录(数据可重复,代表多次购买),1万用户量、1千物品量。
经过多次运行测试、在这个数据量下总运行时间大概在5200±200毫秒,去除数据库的操作以及输出, 程序运行实际时间大概在3700±100毫秒。
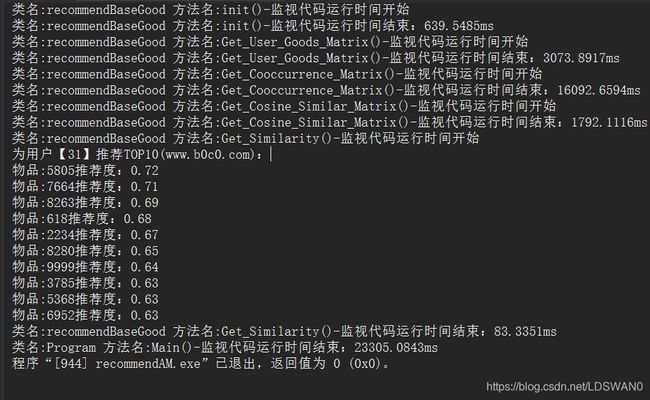
4、往数据库随生成成20万条购买记录(数据可重复,代表多次购买),1万用户量、1万物品量。
在这个数据量下可以看到在物品量增加的情况下,效率很慢。
所以我写的这个算法实现还需要进一步优化。
更新:
由于这个是c#的,不过其实不管什么实现语言,只要知道思路就行,推荐大家去看一下java版的apache开源的推荐系统:mahout。但是还是推荐大家去看一下。不过博主也还一直没看的。
近期有很多人联系我说要源码,其实源码在这个里面已经都写了。少量的一些不重要的我就没放着上面。关于GlobalFunAndVar这个类是我自定义的一个全局类,在这里面就只是用到统计代码运行时间和连接数据库执行sql语句。OutPutArray这个方法是自定义的一个输出二维数组的方法。代码如下:
///
/// 输出指定的二维数组
///
///
public void OutPutArray(T[,] array)
{
bool isDouble = false;
if (array[0, 0] is double)
isDouble = true;
int len1 = array.GetLength(0);
int len2 = array.GetLength(1);
for (int i = 0; i < len1; i++)
{
for (int j = 0; j < len2; j++)
{
//if (j >= i)
switch (isDouble)
{
case false:
Console.Write(array[i, j] + " ");
break;
case true:
if (array[i, j].ToString().Length == 1)
Console.Write(array[i, j] + ".00 ");
else
Console.Write(array[i, j] + " ");
break;
}
/*
else
Console.Write(array[i, j] + " ");
*/
}
Console.WriteLine();
}
} 191221更新(重大更新): 修复执行错误,并给出一个Demo使用样例代码,大家请重新重新下载dll,并可以参考样例代码来进行测试使用。
191108更新:由于我看有人需要,我把这个最终的推荐算法以及一些辅助方法封装成了一个dll,大家只需引入这个dll就可以。
点击进入b0c0.com下载
xml文件为注释,因为只引入dll的话,在vs中调用dll中的方法是没有注释说明的,只需把这个注释xml和dll放在同一目录(dll和xml文件名必须相同!),vs直接引入dll就能显示注释。
方法说明:
一共有两个类接口调用:GlobalFunAndVar(辅助通用类)、RecommendBaseGood(基于物品的推荐接口)
RecommendBaseGood:
///
/// 构造方法(数据初始化)
///
///
/// 第1列为userId 用户id,
/// 第2列为goodId 物品id,
/// 第3列为rating 评分,
///
/// 是否打开调试(只用于输出构建的矩阵结果以及统计运行时间)
public RecommendBaseGood(DataTable dataTable, bool isDeBug);
///
/// 为某个具体用户计算预测兴趣度
///
/// 用户id
/// key:物品id,value:物品推荐度
public Dictionary Get_SimilarityByUser(int user);
///
/// 为所有用户计算预测兴趣度
///
/// key:用户id,value:(key:物品id,推荐度)
public Dictionary> Get_SimilarityAllUser() GlobalFunAndVar:
///
/// 获得指定的MethodBase对象
///
/// 指定是属于谁的的方法
///
/// 监视代码运行时间开始
///
public void stopwatchBegin()
///
/// 监视代码运行时间结束
///
public void stopwatchEnd()
///
/// 指定的sql查询并填充到DataSet返回
///
/// sql语句
/// SqlConnection
///