AVL平衡树--(插入)

为什么要引入AVL平衡树二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，退化成on效率低下。
avl树的定义:
当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之
差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
(1)它的左右子树都是AVL树
(2)左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在logn()以2为底) ，搜索时间复杂度O(logn(以2为底) )
同理avl树也是三叉链

    struct AVLTreeNode{
        5   pair_kv;
        6   AVLTreeNode *_right;
        7   AVLTreeNode *_left;
        8   AVLTreeNode *_pparent;                                                      
        9   int _bf;//平衡因子
       10   AVLTreeNode(const pair&kv)
       11     :_kv(kv),
       12     _right(nullptr),
       13     _left(nullptr),
       14     _pparent(nullptr),
       15     _bf(0)
       }

也是左孩子右孩子+母亲但是还需要平衡因子,
平衡因子就是左右子树的高度差如果平衡因子在-1~1直接则是平衡的如果不是则需要调整
(1)首先建设树
相比较搜索树平衡树的插入比较复杂因为在插入一个结点后要保证平衡本文主要讲的是avl树的插入同理删除一个节点思想也是一样的
当前插入的值比他小在左边比他大在右边
template
struct AVLTreeNode
{
	pair _kv;
	AVLTreeNode* _left;
	AVLTreeNode* _right;
	AVLTreeNode* _parent;

	int _bf; // balance factor

	AVLTreeNode(const pair& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

template
class AVLTree
{
	typedef AVLTreeNode Node;
public:
	bool Insert(const pair& kv)
	{
		// 插入节点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
	}

		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
	// 调平衡
	// 1.更新平衡因子-----------------------<1>

调节平衡因子有四种情况
(1)左旋

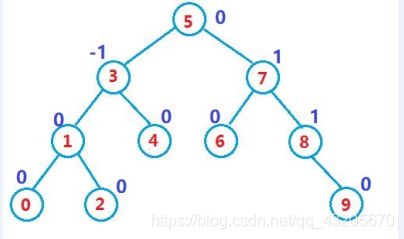
插入后的树结果如下

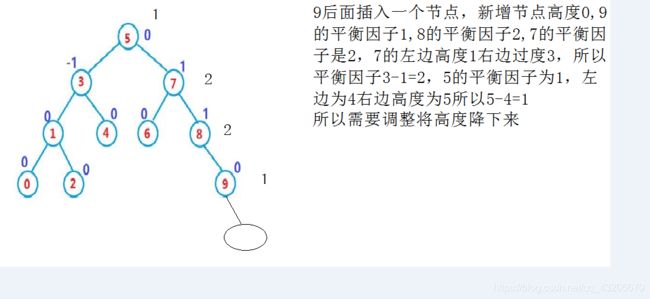
黑色圈为插入的结点
则旋转过程如下8放在9的左边9连接7

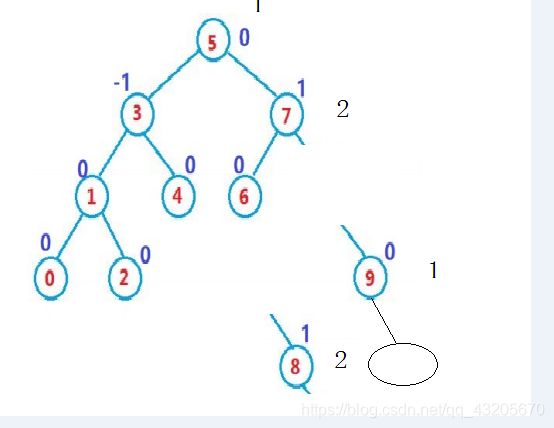
旋转后的结果如下图

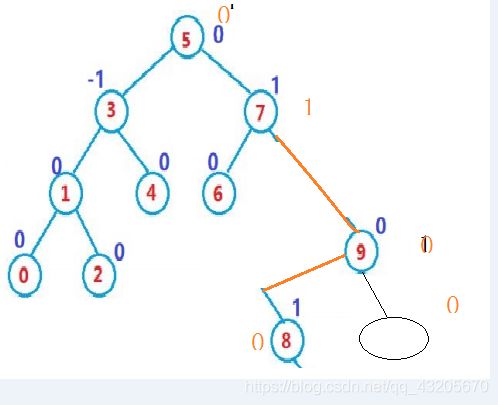
5 7 9 8 的平衡因子依次为0 1 0 0
上图就是左旋抽象图如下左边是原始图在左边的c上插入一个元素(就是蓝色的部分)图上有个黑色的圈表示上面还有可能有结点如果没有结点就是根

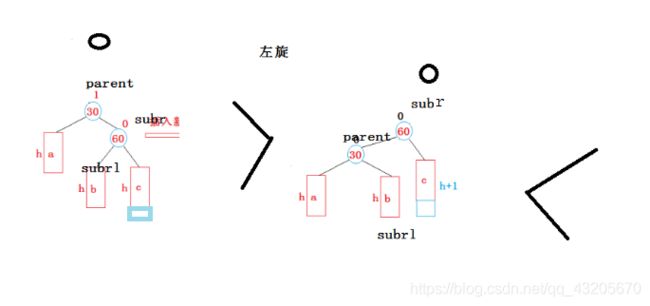
然后根据抽象关系就可以写出左旋代码–直接对图即可
是三叉链
void RotateL(Node* parent){
Nodesubr=parent->_right;
Nodesubrl=subr->left;
//旋转后,subr变成了parent
parent->left=subrl;
//此处要判断旋转后subrl不能为空
if(subrl){
//继续建立连接关系
subrl->_parent=parent;
}
//连接subr和parent
subr->left=parent;
parent->_parent=subr;
Node* ppnode = parent->_parent;
//特殊情况处理parent为根
就是没有母亲结点
if(paren==_root){
//parent没有母亲结点那么调整后根为sur
然后让sur->parent指向空
_root->parent=null;
}else{
//parent 有母亲那么parent有两种情况1是母亲的左孩子2是母亲右孩子----申请一个节点ppnode(表示母亲)
if(ppnode->left==parent){//panrent是左孩子
ppnode->_left=subr;
}else{是右边的孩子
ppnode->_right=subr;
}
subr->parent=ppnode;
}
//平衡因子变成0
parent->_bf = subr->_bf = 0;
}
以上就是左旋代码—需要考虑的问题有(1)parent是否是根(2)parent有母亲是母亲的左孩子还是右孩子(3)subrl不能为空
最后就注意连接关系即可因为是三叉链需要连接6次(3个点来会都要连接)
接下来是右旋是在a的位置+1个结点

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)//右旋要保证subrl不为空
subLR->_parent = parent;
subL->_right = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
if (ppNode == nullptr)//母亲的母亲为空
{
_root = subL;
_root->_parent = nullptr;
}
else
{//祖母不为空可,parent为祖母的左边
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else//parent为祖母的右边
{
ppNode->_right = subL;
}
subL->_parent = ppNode;//从subl连接祖母//旋转后
//subl成了原来的parent
}
parent->_bf = subL->_bf = 0;
}
//接下来是右左旋

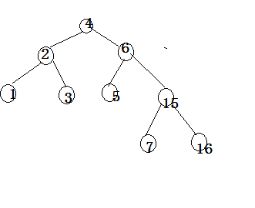
插入结点14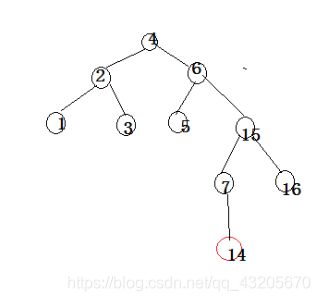

最后结果如图


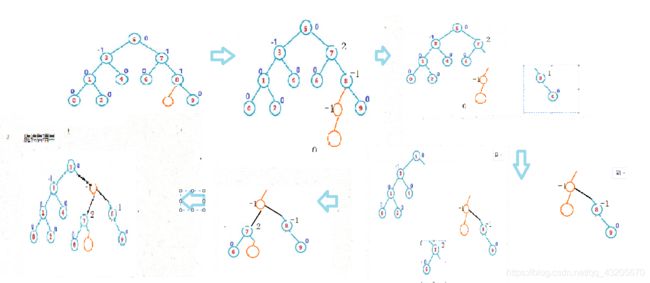
那么右左旋转以后就可以了吗?不可以还需要调节平衡因子
抽象图如下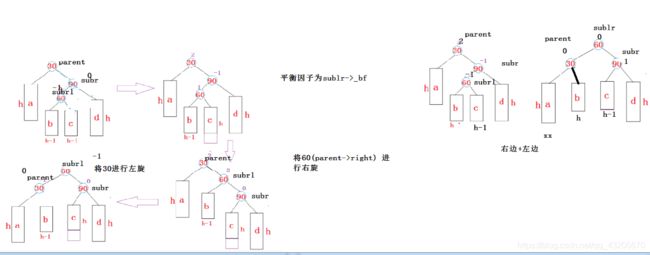
最后只需要关注最右边那幅图起始和调平衡后

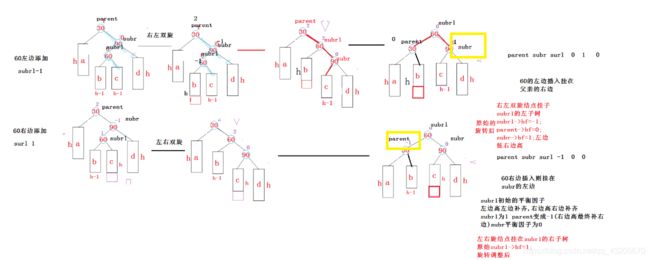
对于此图的上面是右左双旋
在subr的左子树添加一个节点在旋转后parent sur surl平衡因子依次是0 1 0但是还是平衡的
所以平衡因子在旋转后根的平衡因是有可能是-1 0 1三种情况它的决定对于右左旋节点挂在subrl的左树的右边就是parent的右边,旋转后(1)parent=0,但是subr->bf=-1(此图根节点),subrl=1所以bf=-1 时候parent->bf=0,subrl=1;这是一种情况
(2)旋转后parent=-1,subrl=1,subr=0,也是一种情况
同理左右旋
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
parent->_bf = subRL->_bf = subR->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
}
同理可得左右旋的情况:
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
最后进行整体调节平衡因子整体调节与<1>连接起来即可
while (parent)
{
if (cur == parent->_right)//如果在parent的右边则parent的平衡因子会增加
{
parent->_bf++;
}
else
{
parent->_bf–;
}
if (parent->_bf == 0) // 高度不变，更新完成
{
break;
}
else if (abs(parent->_bf) == 1) // 高度变了，继续完成调整
如果pParent的平衡因子为正负1，说明插入前_parent的平衡因子一定为0，插入后被
更新成正负1此时以_parent为根的树的高度增加，需要继续向上更新

		{
			cur = parent;
			parent = parent->_parent;
		}
		else if (abs(parent->_bf) == 2) // 不平衡，旋转
		{
			if (parent->_bf == 2)
			{
				if (cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (cur->_bf == -1)
				{
					RotateRL(parent);
				}
			}
			else if (parent->_bf == -2)
			{
				if (cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if (cur->_bf == 1)
				{
					RotateLR(parent);
				}
			}
			break;
		}
		else
		{
			assert(false);
		}
	}turn true;
	}
	private:
Node* _root = nullptr;

public:
最后进行验证
通过中序遍历来检验左右子树的高度差,这样还不行还只能说明它是二叉搜索树,还需要检验它的平衡因子,
void InOrder()
{
_InOrder(_root);
cout << endl;
}

void _InOrder(Node* root)
{
	if (root == nullptr)
		return;
	_InOrder(root->_left);
	cout << root->_kv.first << " ";
	_InOrder(root->_right);
}
int _Height(Node* root)
{
	if (root == nullptr)
	{
		return 0;
	}
	int leftheight = _Height(root->_left);
	int rightheight = _Height(root->_right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}
bool IsBalance()
{
	return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
	if (root == nullptr)
		return true;
	int leftheight = _Height(root->_left);
	int rightheight = _Height(root->_right);
	if (rightheight-leftheight != root->_bf)
	{
		cout << root->_kv.first << "平衡因子异常" << endl;
		return false;
	}
	return abs(leftheight - rightheight) < 2
		&& _IsBalance(root->_left)
		&& _IsBalance(root->_right);
}

};
void TestAVLTree()
{
AVLTree t;
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, };
for (auto e : a)
{
t.Insert(make_pair(e, e));
}
t.InOrder();
cout << t.IsBalance() << endl;
}