2020.8.11-2020.8.16paddle学习心得体会③

手写数字识别

**数字识别是计算机从纸质文档、照片或其他来源接收、理解并识别可读的数字的能力，目前比较受关注的是手写数字识别。手写数字识别是一个典型的图像分类问题，已经被广泛应用于汇款单号识别、手写邮政编码识别等领域，大大缩短了业务处理时间，提升了工作效率和质量。
在处理如 图1 所示的手写邮政编码的简单图像分类任务时，可以使用基于MNIST数据集的手写数字识别模型。MNIST是深度学习领域标准、易用的成熟数据集，包含60000条训练样本和10000条测试样本。
**

MNIST数据集
MNIST数据集是从NIST的Special Database 3（SD-3）和Special Database 1（SD-1）构建而来。Yann LeCun等人从SD-1和SD-3中各取一半数据作为MNIST训练集和测试集，其中训练集来自250位不同的标注员，且训练集和测试集的标注员完全不同。

MNIST数据集的发布，吸引了大量科学家训练模型。1998年，LeCun分别用单层线性分类器、多层感知器（Multilayer Perceptron, MLP）和多层卷积神经网络LeNet进行实验，使得测试集的误差不断下降（从12%下降到0.7%）。在研究过程中，LeCun提出了卷积神经网络（Convolutional Neural Network，CNN），大幅度地提高了手写字符的识别能力，也因此成为了深度学习领域的奠基人之一。

教程采用"横纵式"教学法，适用于深度学习初学者

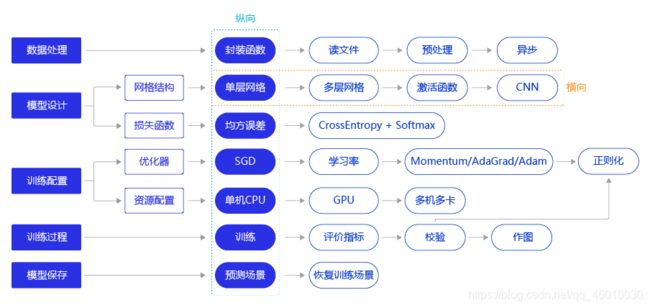
在“横纵式”教学法中，纵向概要介绍模型的基本代码结构和极简实现方案。横向深入探讨构建模型的每个环节中，更优但相对复杂的实现方案。例如在模型设计环节，除了在极简版本使用的单层神经网络（与房价预测模型一样）外，还可以尝试更复杂的网络结构，如多层神经网络、加入非线性的激活函数，甚至专门针对视觉任务优化的卷积神经网络。

实现代码：
#加载飞桨和相关类库
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Linear
import numpy as np
import os
from PIL import Image

#如果～/.cache/paddle/dataset/mnist/目录下没有MNIST数据，API会自动将MINST数据下载到该文件夹下
#设置数据读取器，读取MNIST数据训练集
trainset = paddle.dataset.mnist.train()
#包装数据读取器，每次读取的数据数量设置为batch_size=8
train_reader = paddle.batch(trainset, batch_size=8)

#以迭代的形式读取数据
for batch_id, data in enumerate(train_reader()):
# 获得图像数据，并转为float32类型的数组
img_data = np.array([x[0] for x in data]).astype(‘float32’)
# 获得图像标签数据，并转为float32类型的数组
label_data = np.array([x[1] for x in data]).astype(‘float32’)
# 打印数据形状
print(“图像数据形状和对应数据为:”, img_data.shape, img_data[0])
print(“图像标签形状和对应数据为:”, label_data.shape, label_data[0])
break

print("\n打印第一个batch的第一个图像，对应标签数字为{}".format(label_data[0]))
#显示第一batch的第一个图像
import matplotlib.pyplot as plt
img = np.array(img_data[0]+1)*127.5
img = np.reshape(img, [28, 28]).astype(np.uint8)

plt.figure(“Image”) # 图像窗口名称
plt.imshow(img)
plt.axis(‘on’) # 关掉坐标轴为 off
plt.title(‘image’) # 图像题目
plt.show()

模型设计

下面以类的方式组建手写数字识别的网络，实现方法如下所示。

#定义mnist数据识别网络结构，同房价预测网络
class MNIST(fluid.dygraph.Layer):
def init(self):
super(MNIST, self).init()

    # 定义一层全连接层，输出维度是1，激活函数为None，即不使用激活函数
    self.fc = Linear(input_dim=784, output_dim=1, act=None)
    
# 定义网络结构的前向计算过程
def forward(self, inputs):
    outputs = self.fc(inputs)
    return outputs

训练配置

#定义飞桨动态图工作环境
with fluid.dygraph.guard():
# 声明网络结构
model = MNIST()
# 启动训练模式
model.train()
# 定义数据读取函数，数据读取batch_size设置为16
train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=16)
# 定义优化器，使用随机梯度下降SGD优化器，学习率设置为0.001
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())

训练过程

with fluid.dygraph.guard():
model = MNIST()
model.train()
train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=16)
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
EPOCH_NUM = 10
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，格式需要转换成符合框架要求
image_data = np.array([x[0] for x in data]).astype(‘float32’)
label_data = np.array([x[1] for x in data]).astype(‘float32’).reshape(-1, 1)
# 将数据转为飞桨动态图格式
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)

        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.square_error_cost(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了1000批次的数据，打印下当前Loss的情况
        if batch_id !=0 and batch_id  % 1000 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

# 保存模型
fluid.save_dygraph(model.state_dict(), 'mnist')
**模型测试**
# 导入图像读取第三方库

import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import cv2
import numpy as np
#读取图像
img1 = cv2.imread(’./work/example_0.png’)
example = mpimg.imread(’./work/example_0.png’)
#显示图像
plt.imshow(example)
plt.show()
im = Image.open(’./work/example_0.png’).convert(‘L’)
print(np.array(im).shape)
im = im.resize((28, 28), Image.ANTIALIAS)
plt.imshow(im)
plt.show()
print(np.array(im).shape)

def load_image(img_path):
# 从img_path中读取图像，并转为灰度图
im = Image.open(img_path).convert(‘L’)
print(np.array(im))
im = im.resize((28, 28), Image.ANTIALIAS)
im = np.array(im).reshape(1, -1).astype(np.float32)
# 图像归一化，保持和数据集的数据范围一致
im = 1 - im / 127.5
return im

#定义预测过程
with fluid.dygraph.guard():
model = MNIST()
params_file_path = ‘mnist’
img_path = ‘./work/example_0.png’
#加载模型参数
model_dict, _ = fluid.load_dygraph(“mnist”)
model.load_dict(model_dict)
#灌入数据
model.eval()
tensor_img = load_image(img_path)
result = model(fluid.dygraph.to_variable(tensor_img))
#预测输出取整，即为预测的数字，打印结果
print(“本次预测的数字是”, result.numpy().astype(‘int32’))

数据处理

训练样本乱序、生成批次数据
代码：
imgs, labels = train_set[0], train_set[1]
print("训练数据集数量: ", len(imgs))
#获得数据集长度
imgs_length = len(imgs)
定义数据集每个数据的序号，根据序号读取数据
index_list = list(range(imgs_length))
#读入数据时用到的批次大小
BATCHSIZE = 100

#随机打乱训练数据的索引序号
random.shuffle(index_list)

#定义数据生成器，返回批次数据
def data_generator():

imgs_list = []
labels_list = []
for i in index_list:
    # 将数据处理成期望的格式，比如类型为float32，shape为[1, 28, 28]
    img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
    label = np.reshape(labels[i], [1]).astype('float32')
    imgs_list.append(img) 
    labels_list.append(label)
    if len(imgs_list) == BATCHSIZE:
        # 获得一个batchsize的数据，并返回
        yield np.array(imgs_list), np.array(labels_list)
        # 清空数据读取列表
        imgs_list = []
        labels_list = []

# 如果剩余数据的数目小于BATCHSIZE，
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
    yield np.array(imgs_list), np.array(labels_list)
return data_generator

# 声明数据读取函数，从训练集中读取数据

train_loader = data_generator
#以迭代的形式读取数据
for batch_id, data in enumerate(train_loader()):
image_data, label_data = data
if batch_id == 0:
# 打印数据shape和类型
print(“打印第一个batch数据的维度:”)
print(“图像维度: {}, 标签维度: {}”.format(image_data.shape, label_data.shape))
break

校验数据有效性
机器效验代码：
imgs_length = len(imgs)

assert len(imgs) == len(labels), \
      "length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(label))

人工效验代码：
train_loader = data_generator
#以迭代的形式读取数据
for batch_id, data in enumerate(train_loader()):
image_data, label_data = data
if batch_id == 0:
# 打印数据shape和类型
print(“打印第一个batch数据的维度，以及数据的类型:”)
print(“图像维度: {}, 标签维度: {}, 图像数据类型: {}, 标签数据类型: {}”.format(image_data.shape, label_data.shape, type(image_data), type(label_data)))
break

封装数据读取与处理函数

代码：
def load_data(mode=‘train’):
datafile = ‘./work/mnist.json.gz’
print(‘loading mnist dataset from {} …’.format(datafile))
# 加载json数据文件
data = json.load(gzip.open(datafile))
print(‘mnist dataset load done’)

# 读取到的数据区分训练集，验证集，测试集
train_set, val_set, eval_set = data
if mode=='train':
    # 获得训练数据集
    imgs, labels = train_set[0], train_set[1]
elif mode=='valid':
    # 获得验证数据集
    imgs, labels = val_set[0], val_set[1]
elif mode=='eval':
    # 获得测试数据集
    imgs, labels = eval_set[0], eval_set[1]
else:
    raise Exception("mode can only be one of ['train', 'valid', 'eval']")
print("训练数据集数量: ", len(imgs))

# 校验数据
imgs_length = len(imgs)

assert len(imgs) == len(labels), \
      "length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(label))

# 获得数据集长度
imgs_length = len(imgs)

# 定义数据集每个数据的序号，根据序号读取数据
index_list = list(range(imgs_length))
# 读入数据时用到的批次大小
BATCHSIZE = 100

# 定义数据生成器
def data_generator():
    if mode == 'train':
        # 训练模式下打乱数据
        random.shuffle(index_list)
    imgs_list = []
    labels_list = []
    for i in index_list:
        # 将数据处理成希望的格式，比如类型为float32，shape为[1, 28, 28]
        img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
        label = np.reshape(labels[i], [1]).astype('float32')
        imgs_list.append(img) 
        labels_list.append(label)
        if len(imgs_list) == BATCHSIZE:
            # 获得一个batchsize的数据，并返回
            yield np.array(imgs_list), np.array(labels_list)
            # 清空数据读取列表
            imgs_list = []
            labels_list = []

    # 如果剩余数据的数目小于BATCHSIZE，
    # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
    if len(imgs_list) > 0:
        yield np.array(imgs_list), np.array(labels_list)
return data_generator

异步数据读取&同步数据读取

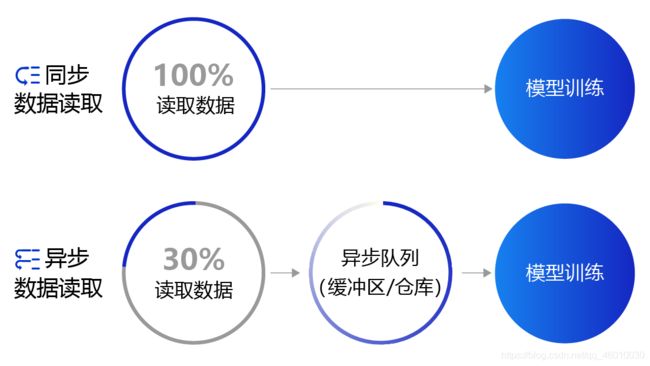
同步数据读取：数据读取与模型训练串行。当模型需要数据时，才运行数据读取函数获得当前批次的数据。在读取数据期间，模型一直等待数据读取结束才进行训练，数据读取速度相对较慢。
异步数据读取：数据读取和模型训练并行。读取到的数据不断的放入缓存区，无需等待模型训练就可以启动下一轮数据读取。当模型训练完一个批次后，不用等待数据读取过程，直接从缓存区获得下一批次数据进行训练，从而加快了数据读取速度。
异步队列：数据读取和模型训练交互的仓库，二者均可以从仓库中读取数据，它的存在使得两者的工作节奏可以解耦。

异步数据读取代码：

#定义数据读取后存放的位置，CPU或者GPU，这里使用CPU
#place = fluid.CUDAPlace(0) 时，数据才读取到GPU上
place = fluid.CPUPlace()
with fluid.dygraph.guard(place):
# 声明数据加载函数，使用训练模式
train_loader = load_data(mode=‘train’)
# 定义DataLoader对象用于加载Python生成器产生的数据
data_loader = fluid.io.DataLoader.from_generator(capacity=5, return_list=True)
# 设置数据生成器
data_loader.set_batch_generator(train_loader, places=place)
# 迭代的读取数据并打印数据的形状
for i, data in enumerate(data_loader):
image_data, label_data = data
print(i, image_data.shape, label_data.shape)
if i>=5:
break
与同步数据读取相比，异步数据读取仅增加了三行代码，如下所示。

place = fluid.CPUPlace()

#设置读取的数据是放在CPU还是GPU上。

data_loader = fluid.io.DataLoader.from_generator(capacity=5, return_list=True)

#创建一个DataLoader对象用于加载Python生成器产生的数据。数据会由Python线程预先读取，并异步送入一个队列中。

data_loader.set_batch_generator(train_loader, place)

#用创建的DataLoader对象设置一个数据生成器set_batch_generator，输入的参数是一个Python数据生成器train_loader和服务器资源类型place（标明CPU还是GPU）

网络结构

经典的全连接神经网络

输入层：将数据输入给神经网络。在该任务中，输入层的尺度为28×28的像素值。
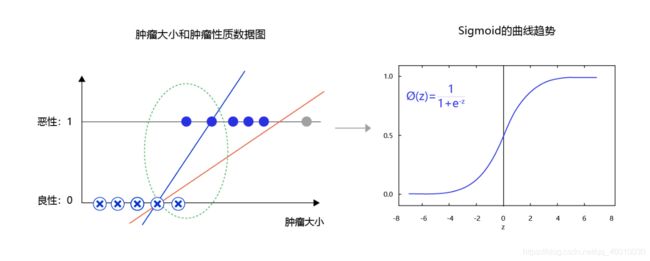
隐含层：增加网络深度和复杂度，隐含层的节点数是可以调整的，节点数越多，神经网络表示能力越强，参数量也会增加。在该任务中，中间的两个隐含层为10×10的结构，通常隐含层会比输入层的尺寸小，以便对关键信息做抽象，激活函数使用常见的sigmoid函数。
输出层：输出网络计算结果，输出层的节点数是固定的。如果是回归问题，节点数量为需要回归的数字数量；如果是分类问题，则是分类标签的数量。在该任务中，模型的输出是回归一个数字，输出层的尺寸为1。

Sigmoid是早期神经网络模型中常见的非线性变换函数，通过如下代码，绘制出Sigmoid的函数曲线。
def sigmoid(x):
# 直接返回sigmoid函数
return 1. / (1. + np.exp(-x))

#param:起点，终点，间距
x = np.arange(-8, 8, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()

下述代码为经典全连接神经网络的实现。完成网络结构定义后，即可训练神经网络。

#多层全连接神经网络实现
class MNIST(fluid.dygraph.Layer):
def init(self):
super(MNIST, self).init()
# 定义两层全连接隐含层，输出维度是10，激活函数为sigmoid
self.fc1 = Linear(input_dim=784, output_dim=10, act=‘sigmoid’) # 隐含层节点为10，可根据任务调整
self.fc2 = Linear(input_dim=10, output_dim=10, act=‘sigmoid’)
# 定义一层全连接输出层，输出维度是1，不使用激活函数
self.fc3 = Linear(input_dim=10, output_dim=1, act=None)

# 定义网络的前向计算
def forward(self, inputs, label=None):
    inputs = fluid.layers.reshape(inputs, [inputs.shape[0], 784])
    outputs1 = self.fc1(inputs)
    outputs2 = self.fc2(outputs1)
    outputs_final = self.fc3(outputs2)
    return outputs_final

#网络结构部分之后的代码，保持不变
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数，获得MNIST训练数据集
train_loader = load_data(‘train’)
# 使用SGD优化器，learning_rate设置为0.01
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
# 训练5轮
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)

        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.square_error_cost(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

卷积神经网络

虽然使用经典的全连接神经网络可以提升一定的准确率，但对于计算机视觉问题，效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化，更适合处理视觉问题。卷积神经网络由多个卷积层和池化层组成，如 图 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示，池化层对这些特征表示进行过滤，保留最关键的特征信息。

两层卷积和池化的卷积神经网络实现如下所示。

#多层卷积神经网络实现
class MNIST(fluid.dygraph.Layer):
def init(self):
super(MNIST, self).init()

     # 定义卷积层，输出特征通道num_filters设置为20，卷积核的大小filter_size为5，卷积步长stride=1，padding=2
     # 激活函数使用relu
     self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
     # 定义池化层，池化核pool_size=2，池化步长为2，选择最大池化方式
     self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
     # 定义卷积层，输出特征通道num_filters设置为20，卷积核的大小filter_size为5，卷积步长stride=1，padding=2
     self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
     # 定义池化层，池化核pool_size=2，池化步长为2，选择最大池化方式
     self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
     # 定义一层全连接层，输出维度是1，不使用激活函数
     self.fc = Linear(input_dim=980, output_dim=1, act=None)
     
# 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
 def forward(self, inputs):
     x = self.conv1(inputs)
     x = self.pool1(x)
     x = self.conv2(x)
     x = self.pool2(x)
     x = fluid.layers.reshape(x, [x.shape[0], -1])
     x = self.fc(x)
     return x

训练定义好的卷积神经网络，如下所示。

#网络结构部分之后的代码，保持不变
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data(‘train’)
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)

        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.square_error_cost(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

比较经典全连接神经网络和卷积神经网络的损失变化，可以发现卷积神经网络的损失值下降更快，且最终的损失值更小。

损失函数

损失函数是模型优化的目标，用于在众多的参数取值中，识别最理想的取值。损失函数的计算在训练过程的代码中，每一轮模型训练的过程都相同，分如下三步：

1.先根据输入数据正向计算预测输出。
2.再根据预测值和真实值计算损失。
3.最后根据损失反向传播梯度并更新参数。

分类任务的损失函数

1.房价预测是回归任务，而手写数字识别是分类任务，使用均方误差作为分类任务的损失函数存在逻辑和效果上的缺欠。
2.房价可以是大于0的任何浮点数，而手写数字识别的输出只可能是0-9之间的10个整数，相当于一种标签。
3.在房价预测的案例中，由于房价本身是一个连续的实数值，因此以模型输出的数值和真实房价差距作为损失函数（loss）是符合道理的。但对于分类问题，真实结果是分类标签，而模型输出是实数值，导致以两者相减作为损失不具备物理含义。

Softmax函数

如果模型能输出10个标签的概率，对应真实标签的概率输出尽可能接近100%，而其他标签的概率输出尽可能接近0%，且所有输出概率之和为1。这是一种更合理的假设！与此对应，真实的标签值可以转变成一个10维度的one-hot向量，在对应数字的位置上为1，其余位置为0，比如标签“6”可以转变成[0,0,0,0,0,0,1,0,0,0]。

为了实现上述思路，需要引入Softmax函数，它可以将原始输出转变成对应标签的概率。公式如下，其中C是标签类别个数。

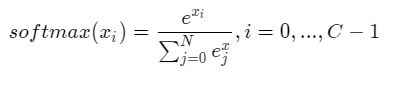
举例图示

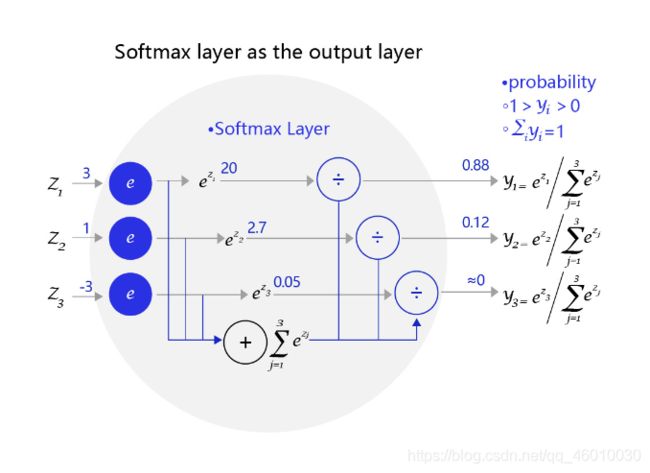
交叉熵

在模型输出为分类标签的概率时，直接以标签和概率做比较也不够合理，人们更习惯使用交叉熵误差作为分类问题的损失衡量。

交叉熵损失函数的设计是基于最大似然思想：最大概率得到观察结果的假设是真的。

经过公式推导，使得上述概率最大等价于最小化交叉熵，得到交叉熵的损失函数。交叉熵的公式如下：

交叉熵的代码实现

#修改标签数据的格式，从float32到int64
import os
import random
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
from PIL import Image

import gzip
import json

#定义数据集读取器
def load_data(mode=‘train’):

# 数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
train_set, val_set, eval_set = data

# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28

if mode == 'train':
    imgs = train_set[0]
    labels = train_set[1]
elif mode == 'valid':
    imgs = val_set[0]
    labels = val_set[1]
elif mode == 'eval':
    imgs = eval_set[0]
    labels = eval_set[1]

imgs_length = len(imgs)

assert len(imgs) == len(labels), \
      "length of train_imgs({}) should be the same as train_labels({})".format(
              len(imgs), len(labels))

index_list = list(range(imgs_length))

# 读入数据时用到的batchsize
BATCHSIZE = 100

# 定义数据生成器
def data_generator():
    if mode == 'train':
        random.shuffle(index_list)
    imgs_list = []
    labels_list = []
    for i in index_list:
        img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
        label = np.reshape(labels[i], [1]).astype('int64')
        imgs_list.append(img) 
        labels_list.append(label)
        if len(imgs_list) == BATCHSIZE:
            yield np.array(imgs_list), np.array(labels_list)
            imgs_list = []
            labels_list = []

    # 如果剩余数据的数目小于BATCHSIZE，
    # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
    if len(imgs_list) > 0:
        yield np.array(imgs_list), np.array(labels_list)

return data_generator

在网络定义部分，需要修改输出层结构，代码如下所示。*
从：self.fc = Linear(input_dim=980, output_dim=1, act=None)
到：self.fc = Linear(input_dim=980, output_dim=10, act=‘softmax’)

#定义模型结构
class MNIST(fluid.dygraph.Layer):
def init(self):
super(MNIST, self).init()

     # 定义一个卷积层，使用relu激活函数
     self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
     # 定义一个池化层，池化核为2，步长为2，使用最大池化方式
     self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
     # 定义一个卷积层，使用relu激活函数
     self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
     # 定义一个池化层，池化核为2，步长为2，使用最大池化方式
     self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
     # 定义一个全连接层，输出节点数为10 
     self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 定义网络的前向计算过程
 def forward(self, inputs):
     x = self.conv1(inputs)
     x = self.pool1(x)
     x = self.conv2(x)
     x = self.pool2(x)
     x = fluid.layers.reshape(x, [x.shape[0], 980])
     x = self.fc(x)
     return x

修改计算损失的函数，从均方误差（常用于回归问题）到交叉熵误差（常用于分类问题），代码如下所示。
从：loss = fluid.layers.square_error_cost(predict, label)
到：loss = fluid.layers.cross_entropy(predict, label)

#仅修改计算损失的函数，从均方误差（常用于回归问题）到交叉熵误差（常用于分类问题）
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data(‘train’)
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)

        #前向计算的过程
        predict = model(image)
        
        #计算损失，使用交叉熵损失函数，取一个批次样本损失的平均值
        loss = fluid.layers.cross_entropy(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

由于我们修改了模型的输出格式，因此使用模型做预测时的代码也需要做相应的调整。从模型输出10个标签的概率中选择最大的，将其标签编号输出。

#读取一张本地的样例图片，转变成模型输入的格式
def load_image(img_path):
# 从img_path中读取图像，并转为灰度图
im = Image.open(img_path).convert(‘L’)
im.show()
im = im.resize((28, 28), Image.ANTIALIAS)
im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)
# 图像归一化
im = 1.0 - im / 255.
return im

#定义预测过程
with fluid.dygraph.guard():
model = MNIST()
params_file_path = ‘mnist’
img_path = ‘./work/example_0.jpg’
# 加载模型参数
model_dict, _ = fluid.load_dygraph(“mnist”)
model.load_dict(model_dict)

model.eval()
tensor_img = load_image(img_path)
#模型反馈10个分类标签的对应概率
results = model(fluid.dygraph.to_variable(tensor_img))
#取概率最大的标签作为预测输出
lab = np.argsort(results.numpy())
print("本次预测的数字是: ", lab[0][-1])

优化算法

设置学习率
学习率不是越小越好。学习率越小，损失函数的变化速度越慢，意味着我们需要花费更长的时间进行收敛，如 图左图所示。
学习率不是越大越好。只根据总样本集中的一个批次计算梯度，抽样误差会导致计算出的梯度不是全局最优的方向，且存在波动。在接近最优解时，过大的学习率会导致参数在最优解附近震荡，损失难以收敛，如 图右图所示。

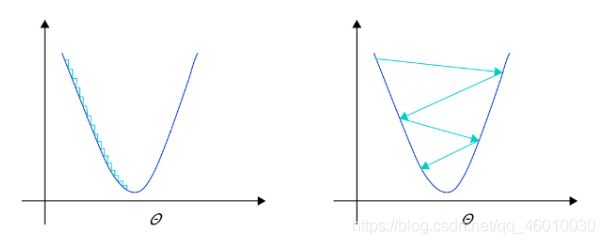
在训练前，我们往往不清楚一个特定问题设置成怎样的学习率是合理的，因此在训练时可以尝试调小或调大，通过观察Loss下降的情况判断合理的学习率，设置学习率的代码如下所示。
#仅优化算法的设置有所差别
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data(‘train’)

#设置不同初始学习率
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
# optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
# optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.1, parameter_list=model.parameters())

EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
    for batch_id, data in enumerate(train_loader()):
        #准备数据，变得更加简洁
        image_data, label_data = data
        image = fluid.dygraph.to_variable(image_data)
        label = fluid.dygraph.to_variable(label_data)
        
        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.cross_entropy(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

学习率的主流优化算法
SGD： 随机梯度下降算法，每次训练少量数据，抽样偏差导致参数收敛过程中震荡。

Momentum： 引入物理“动量”的概念，累积速度，减少震荡，使参数更新的方向更稳定。

AdaGrad： 根据不同参数距离最优解的远近，动态调整学习率。学习率逐渐下降，依据各参数变化大小调整学习率。

Adam： 由于动量和自适应学习率两个优化思路是正交的，因此可以将两个思路结合起来，这就是当前广泛应用的算法。

我们可以尝试选择不同的优化算法训练模型，观察训练时间和损失变化的情况，代码实现如下。

#仅优化算法的设置有所差别
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data(‘train’)

#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())

EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
    for batch_id, data in enumerate(train_loader()):
        #准备数据，变得更加简洁
        image_data, label_data = data
        image = fluid.dygraph.to_variable(image_data)
        label = fluid.dygraph.to_variable(label_data)
        
        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.cross_entropy(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

资源配置

单GPU训练
飞桨动态图通过fluid.dygraph.guard(place=None)里的place参数，设置在GPU上训练还是CPU上训练。

with fluid.dygraph.guard(place=fluid.CPUPlace())　#设置使用CPU资源训神经网络。
with fluid.dygraph.guard(place=fluid.CUDAPlace(0))　#设置使用GPU资源训神经网络，默认使用服务器的第一个GPU卡。"0"是GPU卡的编号，比如一台服务器有的四个GPU卡，编号分别为０、１、２、３。

CPU：fluid.CPUPlace() PRC通信方式（管理员）
GPU：fluid.CUDAPlace(参数0,1,2,3) NCCL通信方式（无管理员，直接大家共享）

代码如下。

#仅前3行代码有所变化，在使用GPU时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()

with fluid.dygraph.guard(place):
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data(‘train’)

#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())

EPOCH_NUM = 2
for epoch_id in range(EPOCH_NUM):
    for batch_id, data in enumerate(train_loader()):
        #准备数据，变得更加简洁
        image_data, label_data = data
        image = fluid.dygraph.to_variable(image_data)
        label = fluid.dygraph.to_variable(label_data)
        
        #前向计算的过程
        predict = model(image)
        
        #计算损失，取一个批次样本损失的平均值
        loss = fluid.layers.cross_entropy(predict, label)
        avg_loss = fluid.layers.mean(loss)
        
        #每训练了200批次的数据，打印下当前Loss的情况
        if batch_id % 200 == 0:
            print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
        
        #后向传播，更新参数的过程
        avg_loss.backward()
        optimizer.minimize(avg_loss)
        model.clear_gradients()

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')

分布式训练

在工业实践中，很多较复杂的任务需要使用更强大的模型。强大模型加上海量的训练数据，经常导致模型训练耗时严重。比如在计算机视觉分类任务中，训练一个在ImageNet数据集上精度表现良好的模型，大概需要一周的时间，因为过程中我们需要不断尝试各种优化的思路和方案。如果每次训练均要耗时1周，这会大大降低模型迭代的速度。在机器资源充沛的情况下，建议采用分布式训练，大部分模型的训练时间可压缩到小时级别。分布式训练有两种实现模式：模型并行和数据并行。

模型并行

模型并行是将一个网络模型拆分为多份，拆分后的模型分到多个设备上（GPU）训练，每个设备的训练数据是相同的。模型并行的实现模式可以节省内存，但是应用较为受限。

模型并行的方式一般适用于如下两个场景：

1.模型架构过大： 完整的模型无法放入单个GPU。如2012年ImageNet大赛的冠军模型AlexNet是模型并行的典型案例，由于当时GPU内存较小，单个GPU不足以承担AlexNet，因此研究者将AlexNet拆分为两部分放到两个GPU上并行训练。

2.网络模型的结构设计相对独立： 当网络模型的设计结构可以并行化时，采用模型并行的方式。如在计算机视觉目标检测任务中，一些模型（如YOLO9000）的边界框回归和类别预测是独立的，可以将独立的部分放到不同的设备节点上完成分布式训练。

数据并行

数据并行与模型并行不同，数据并行每次读取多份数据，读取到的数据输入给多个设备（GPU）上的模型，每个设备上的模型是完全相同的，飞桨采用的就是这种方式。

AI Studio当前仅支持单卡GPU，因此本案例需要在本地GPU上执行，无法在AI Studio上演示。

在启动训练前，需要配置如下参数：

从环境变量获取设备的ID，并指定给CUDAPlace。
device_id = fluid.dygraph.parallel.Env().dev_id
place = fluid.CUDAPlace(device_id)
对定义的网络做预处理，设置为并行模式。
strategy = fluid.dygraph.parallel.prepare_context() ## 新增
model = MNIST()
model = fluid.dygraph.parallel.DataParallel(model, strategy) ## 新增
定义多GPU训练的reader，不同ID的GPU加载不同的数据集。
valid_loader = paddle.batch(paddle.dataset.mnist.test(), batch_size=16, drop_last=true)
valid_loader = fluid.contrib.reader.distributed_batch_reader(valid_loader)
收集每批次训练数据的loss，并聚合参数的梯度。
avg_loss = model.scale_loss(avg_loss) ## 新增
avg_loss.backward()
mnist.apply_collective_grads() ## 新增

完整代码如下。

def train_multi_gpu():

##修改1-从环境变量获取使用GPU的序号
place = fluid.CUDAPlace(fluid.dygraph.parallel.Env().dev_id)

with fluid.dygraph.guard(place):

    ##修改2-对原模型做并行化预处理
    strategy = fluid.dygraph.parallel.prepare_context()
    model = MNIST()
    model = fluid.dygraph.parallel.DataParallel(model, strategy)

    model.train()

    #调用加载数据的函数
    train_loader = load_data('train')
    ##修改3-多GPU数据读取，必须确保每个进程读取的数据是不同的
    train_loader = fluid.contrib.reader.distributed_batch_reader(train_loader)

    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据
            image_data, label_data = data
            image = fluid.dygraph.to_variable(image_data)
            label = fluid.dygraph.to_variable(label_data)

            predict = model(image)

            loss = fluid.layers.cross_entropy(predict, label)
            avg_loss = fluid.layers.mean(loss)

            # 修改4-多GPU训练需要对Loss做出调整，并聚合不同设备上的参数梯度
            avg_loss = model.scale_loss(avg_loss)
            avg_loss.backward()
            model.apply_collective_grads()
            # 最小化损失函数，清除本次训练的梯度
            optimizer.minimize(avg_loss)
            model.clear_gradients()
            
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))

#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')