【机器学习】回归算法-精讲

回归算法

数据类型分为连续型和离散型。离散型的数据经常用来表示分类，连续型的数据经常用来表示不确定的值。比如一个产品质量分为1类，2类，这是离散型。房价1.4万/平，3.4万/平，这是连续型。之前我们学的都是分类，那么对于一些连续型的数据，我们就可以通过回归算法来进行预测了。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。那么什么是线性关系和非线性关系？

线性回归和非线性回归：

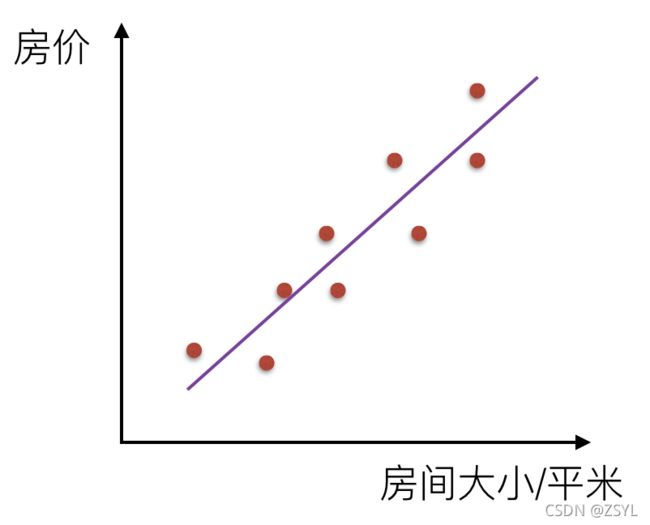
比如说在房价上，房子的面积和房子的价格有着明显的关系。那么X=房间大小，Y=房价，那么在坐标系中可以看到这些点：

如果房间面积大小和房价的关系可以用一根直线表示，那么这就是线性关系：

而如果不是一根直线，那么就是非线性关系：

线性回归

线性回归通过一个或者多个自变量与因变量之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。

线性回归方程：

线性回归方程，就是有k个特征，然后每个特征都有相应的系数，并且在所有特征值为0的情况下，目标值有一个默认值。因此线性回归方程如下：
$$h(w)=w₀+w₁\ast x₁+w₂\ast x₂+\dots$$
整合后的公式为：
$$h(w)=\sum _i^n{w}_{i}xi={\theta }^{T}x$$

损失函数：

损失函数是一个贯穿整个机器学习重要的一个概念，大部分机器学习算法都会有误差，我们得通过显性的公式来描述这个误差，并且将这个误差优化到最小值。

假设现在真实的值为y，预测的值为h，那么损失函数的公式如下：
$$J(\theta )=\frac{1}{2}\sum _i^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2$$

也就是所有误差和的平方。损失函数值越小，说明误差越小.这个损失函数也有一个专门的叫法，叫做最小二乘法。

---

损失函数推理过程：

公式转换：

首先，我们是想要获取到这样一个公式：
$$h(\theta )={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2+\dots$$
那么为了更好的计算，我们将这个公式进行一些变形，将$w_0$后面加个$x_0$，只不过这个$x_0$是为1。所以可以变化成以下：
$$h(\theta )=\sum _i^n{\theta }_i{x}_i$$
而${\theta }_i$和$x_i$可以写成一个矩阵：
$\left[\begin{array}{c}{\theta }_0{\theta }_1{\theta }_3...\end{array}\right]$ x $\left[\begin{array}{c}1\\ x_1\\ x_3\\ ...\end{array}\right]$ = ${\sum }_i^n{\theta }_i{x}_i$ = ${\theta }^{T}x$

用矩阵主要是方便计算。

误差公式：

其次，以上求得的，只是一个预测的值，而不是真实的值，他们中间肯定会存在误差，因此会有以下公式：
$$y_i={\theta }_i{x}_i+{ϵ}_i$$
我们要做的，就是找出最小的${ϵ}_i$，使得预测值和真实值的差距最小。

转化为θ求解：

然后，${ϵ}_i$是存在正数，也存在负数，所以可以简单的把这个数据集，看做是一个服从均值为0，方差为${\sigma }^2$的正态分布。所以${ϵ}_i$出现的概率为：

$$p({ϵ}_i)=\frac{1}{\sqrt{2\pi }\sigma }exp\frac{-({ϵ}_i{)}^2}{2{\sigma }^2}$$

把${ϵ}_i=y_i-{\theta }_i{x}_i$代入到以上高斯分布的函数中，变成以下式子：

$$p({ϵ}_i)=\frac{1}{\sqrt{2\pi }\sigma }exp\frac{-(y_i-{\theta }_i{x}_i{)}^2}{2{\sigma }^2}$$

所以我们就成功的将误差的求解，转换成了θ的求解了。
我们应该求$p({ϵ}_i)$最大的时候的θ。（PS：用贷款的例子理解一下，银行给人贷款，多贷或少贷几百，都是很正常的，但是如果多贷或者少贷太多，从正态分布来说，概率很小。而把银行贷款，多贷和少贷看成是误差，那么我们肯定是想要误差小的，因此也就是要求出现的最大的概率的误差值。

似然函数求θ：

似然函数的主要作用，就是在已经知道变量x的情况下，调整θ，使得概率y的值最大。

以抛硬币为例，假设你拿到了一枚硬币，正常来说一枚均匀的硬币出现正反面的概率应该相同，都是 0.5 ，但是你不确定这枚材质、重量分布情况，需要判断其是否真的是均匀分布。
所以，这里假设这枚硬币有 θ 的概率会正面向上，有 1-θ 的概率反面向上。

为了获得 θ 的值，你做了一个实验：将硬币抛 10 次，得到了一个正反序列 x=HHTTHTHHHH 。这次实验满足二项分布，那么出现这个序列的概率为 θθ(1-θ)(1-θ)θ(1-θ)θθθθ = θ^7(1-θ)3 。

到此为止，我们根据一次简单的二项分布实验，得到了一个关于 θ 的函数，这实际上就是一个似然函数，当 θ 为 0 或者 1 时，对应的概率为 0 ；而当 θ 值为 1/2 时，对应的概率为 1/1024 … …
可以根据不同的 θ 值，绘制出一条曲线，这个曲线就是 θ 的似然函数，而 y 轴表示出现这一现象的概率。

单纯对于这次实验来说，因为这一现象已经出现，那么可以相信，在似然函数最大值所在的 θ 评估为目前认为的合理 θ 值，也即是 0.7 。但是，你不能得出最终的结论 θ = 0.7。因为这里仅仅试验了一次，得到的样本太少，所以最终求出的最大似然值偏差较大，如果经过多次试验，扩充样本空间，则最终求得的最大似然估计可能将接近真实值 0.5 。

引用自：https://jin-yang.github.io/post/math-statistics-likelihood-function-introduce.html。

所以以上，我们可以得出求θ的似然函数为：

$$L(\theta )=\prod _i^m\frac{1}{\sqrt{2\pi }\sigma }exp\frac{-(y_i-{\theta }_i{x}_i{)}^2}{2{\sigma }^2}$$

对数似然：

累乘的方式不太方便我们去求解θ，那么我们可以转换成对数似然，也就是将以上公式放到对数中，然后就可以转换成一个加法运算：

$$log(L(\theta ))=log\prod _i^m\frac{1}{\sqrt{2\pi }\sigma }exp\frac{-(y_i-{\theta }_i{x}_i{)}^2}{2{\sigma }^2}=\sum _i^{n}log\frac{1}{\sqrt{2\pi }\sigma }exp\frac{-(y_i-{\theta }_i{x}_i{)}^2}{2{\sigma }^2}$$

以上公式进行化简后得出：

$$log(L(\theta ))=nlog\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{{\sigma }^2}\ast \frac{1}{2}\sum _i^n(y_i-{\theta }_i{x}_i{)}^2$$

在这里我们不用去关心log后的值会改变，因为我们不是要去求极值，而是要去求极值点。

损失函数：

我们是想要把上面式子求得最大值，然后再获取最大值时候的θ。而上面式子中减号前面的$nlog\frac{1}{\sqrt{2\pi }\sigma }$是一个常数项，所以只要把减号后面的变得最小即可，而减号后面的部分，可以把常数项$\frac{1}{{\sigma }^2}$去掉，因此得到最终的损失函数为：

$$J(\theta )=\frac{1}{2}\sum _i^n(y_i-{\theta }_i{x}_i{)}^2$$

可能有的同学会说，上面其他常数项都能直接约掉，为什么1/2不约掉，原因是为了方便后期求偏导留下的。

损失函数越小，那么说明预测的值是越接近真实值。这个损失函数也叫作最小二乘法。

梯度下降：

梯度下降，非常通俗的理解就是，把对以上“损失函数”最小值的求解，形象的比喻成梯子，然后不断的下降，直到找到最低的值。我们以上图为例，上图中有两个维度，我们要做的，就是求出两个维度上${\theta }_0$和${\theta }_1$，使得损失函数最小。

批量梯度下降（BGD）：

批量梯度下降，是在每次求解过程中，把所有数据都进行考察，因此损失函数应该要在损失函数中加上一个$m$，来求平均值： $J(\theta )=\frac{1}{2m}{\sum }_i^m({\theta }_i{x}_i-y_i{)}^2$
我们要去求一个点的方向，也就是要去求他的斜率，而对这个点求导数，就是他的斜率。所以我们只要求出J(θ)的导数就知道他要往哪个方向下降了。J(θ)的导数为：

$$\frac{\partial J(\theta )}{\partial {\theta }_j}=-\frac{1}{m}\sum _i^m(y^j-h_{\theta }(x^i))x_j^i$$

导数的方向，都是往上走的，现在我们要往梯度下降，因此在以上式子前面加个负号，就得到了下降的方向，而下降是在当前点的基础之上下降的，因此下降后的点为：

$${\theta }_j^{‘}={\theta }_j+\frac{1}{m}\sum _i^m(y^j-h_{\theta }(x^i))x_j^i$$

以此循环，直到找到最低的点。

随机梯度下降（SGD）：

以上是批量梯度下降，每次下降一个点，都要把所有数据都计算一遍，如果数据量少还可以说，但是如果数据量特别大，那么会导致训练的过程会非常耗时。因此我们有另外一种解决方法叫做随机梯度下降：

$${\theta }_j^{‘}={\theta }_j+(y^j-h_{\theta }(x^i))x_j^i$$

随机梯度下降是通过每个样本来迭代更新一次，对比上面的批量梯度下降，迭代一次需要用到所有训练样本（往往如今真实问题训练数据都是非常巨大），一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

mini-batch小批量梯下降MBGD：

我们从上面两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。

$${\theta }_j^{‘}={\theta }_j+\alpha \frac{1}{n}\sum _i^n(y^j-h_{\theta }(x^i))x_j^i$$

这里面有一个α，用来表示学习速率，每次下降的多少。

线性回归案例：

我们用线性回归来预测波士顿房价。正规方程的线性回归用的是sklearn.linear_model.LinearRegression，梯度下降用的是sklearn.linear_model.SGDRegressor。并且在预测完成后，我们想要知道预测的好坏的指标，可以通过以下几种方式进行判别：

1. 均方误差：sklearn.metrics.mean_squared_error(y_true, y_pred)。（误差平方和的均值）。
2. 平均绝对误差：sklearn.metrics.mean_absolute_error(y_true, y_pred)（误差的平均）。

都是越小越好。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error

# 加载数据
boston = load_boston()
# 分割数据
feature_train,feature_test,target_train,target_test = train_test_split(boston.data,boston.target)

# 标准化数据
scaler_feature = StandardScaler()
feature_train = scaler_feature.fit_transform(feature_train)
feature_test = scaler_feature.transform(feature_test)

scaler_target = StandardScaler()
target_train = scaler_target.fit_transform(target_train.reshape(-1,1))
target_test = scaler_target.transform(target_test.reshape(-1,1))

# 线性回归(正规方程)
linear = LinearRegression()
linear.fit(feature_train,target_train)
predict_target_test = scaler_target.inverse_transform(linear.predict(feature_test))
# 计算下正规方程的效果
mean_squared_error(scaler_target.inverse_transform(target_test),predict_target_test)
平均误差： 3.5551177273809675
均方误差： 23.398991931904934

# 线性回归（梯度下降）
sgd = SGDRegressor()
sgd.fit(feature_train,target_train)
# inverse_transform(X_scaled)是将标准化后的数据转换为原始数据。
predict_target_test = scaler_target.inverse_transform(sgd.predict(feature_test))
# 计算下梯度下降的效果
mean_squared_error(scaler_target.inverse_transform(target_test),predict_target_test)

sgd = SGDRegressor()
sgd.fit(X_train,y_train)
y_predict = sgd.predict(X_test)
print("平均误差：",mean_absolute_error(y_test,y_predict))
print("均方误差：",mean_squared_error(y_test,y_predict))
print(sgd.coef_)
print(sgd.intercept_)

平均误差： 3.529515670299321
均方误差： 26.251415587814122
[-0.87227423  0.37914079 -0.40098034  0.53969983 -0.58406232  3.51620633
 -0.53168955 -1.77872109  0.64529551 -0.49328478 -1.86208871  1.16501472
 -3.19140456]
[21.95477955]

正则化与岭回归：

正则化出现的目标，就是为了防止过拟合的现象，公式如下：

$$J(\theta )=MSE(\theta )+\lambda \frac{1}{2}\sum _i^n{\theta }_i^2$$

λ越大，加号后面部分越大，而我们想要的是最小的。因此λ越大，说明惩罚力度是越大的。但是并不是越大越好，太大了，可能会导致模型处理拟合得不好，导致最终预测评分更低。
岭回归，就是加入了正则惩罚项的回归，可以用sklearn.linear_model.Ridge来实现：

from sklearn.linear_model import Ridge

ridge = Ridge(alpha=1)
ridge.fit(X_train,y_train)
y_predict = ridge.predict(X_test)
print("平均误差：",mean_absolute_error(y_test,y_predict))
print("均方误差：",mean_squared_error(y_test,y_predict))

平均误差： 3.5483844638304287
均方误差： 23.582466794809744
[-0.87227423  0.37914079 -0.40098034  0.53969983 -0.58406232  3.51620633
 -0.53168955 -1.77872109  0.64529551 -0.49328478 -1.86208871  1.16501472
 -3.19140456]
[21.95477955]

总结：

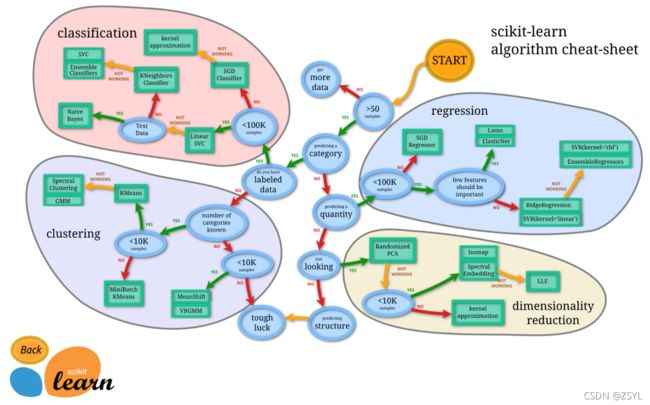
通过上图我们可以发现，当数据量小于10W的时候，正规方程，否则就选择SGD。也就是说在数据量比较少的情况下，正规方程更有优势，在数据量比较大的时候SGD会更加准确。

逻辑回归

逻辑回归（Logistic Regression），简称LR。它的特点是能够是我们的特征输入集合转化为0和1这两类的概率。一般来说，回归不用在分类问题上，但逻辑回归却在二分类问题上表现很好。逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层Sigmod函数映射，即先把特征线性求和，然后使用Sigmoid函数将最为假设函数来概率求解，再进行分类。

Sigmoid函数为：
$$g(z)=\frac{1}{1+e^{-z}}$$
其中的z就是我们使用模型预测的结果。

精确率和召回率：

1. 精确率：预测结果为正例样本中真实为正例的比例（查得准）。公式为：P=TP/(TP+FP)
2. 召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）。公式为：R=TP/(TP+FN)
3. 综合指标F1：P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure。公式为：$F1=\frac{2\ast P\ast R}{P+R}$。

癌症患者逻辑回归案例：

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report

# 地址路径
names = ["Sample code number ","Clump Thickness","Uniformity of Cell Size","Uniformity of Cell Shape","Marginal Adhesion","Single Epithelial Cell Size","Bare Nuclei","Bland Chromatin","Mitoses","Class"]
breast = pd.read_csv("./data/breast-cancer-wisconsin.data",names=names)
breast = breast.replace(to_replace="?",value=np.nan)
breast = breast.dropna()

# 切分数据
x_train,x_test,y_train,y_test = train_test_split(breast[names[1:-1]],breast[names[-1]],test_size=0.25)

# 标准化数据
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

# 逻辑回归
lg = LogisticRegression(C=1.0)
lg.fit(x_train,y_train)
y_predict = lg.predict(x_test)
print("准确率：",lg.score(x_test,y_test))
print("召回率：",classification_report(y_test,y_predict,labels=[2,4],target_names=['良性','恶性']))

准确率： 0.9415204678362573

              precision    recall  f1-score   support

          良性       0.94      0.97      0.95       104
          恶性       0.95      0.90      0.92        67

   micro avg       0.94      0.94      0.94       171
   macro avg       0.94      0.93      0.94       171
weighted avg       0.94      0.94      0.94       171

逻辑回归总结：

1. 优点：适合需要得到一个分类概率的场景，简单，速度快。
2. 缺点：只能用来处理二分类问题，不好处理多分类问题。
3. 应用：是否患病、金融诈骗、是否为虚假账号。

---

加油!

感谢!

努力!