一、直接插入排序
基本思想:
将一个记录插入到已排序的有序表中,使插入后的表仍然有序
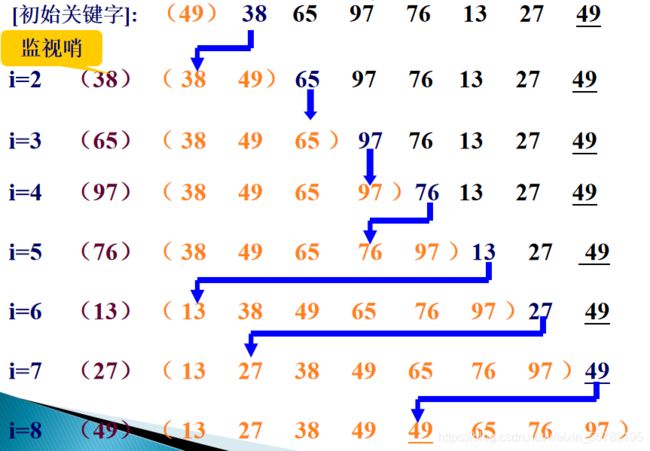
对初始关键字{49 38 65 97 76 13 27 49}进行直接插入排序
package Sort;
//插入排序
public class InsertSort {
public static void main(String[] args) {
int [] arr={49,38,65,97,76,13,27,49};
sort(arr);
print(arr);
}
private static void sort(int [] arr) {
for (int i = 1; i < arr.length; i++) {
for(int j=i;j>0;j--){
if(arr[j]
13 27 38 49 49 65 76 97
Process finished with exit code 0
二、 希尔排序
希尔排序又称“缩小增量排序”(Diminishing Increment Sort))属于插入排序类。
基本思想:
先将整个待排序的记录分割成若干子序列分别进行“直接插入排序”,待整个序列中的记录”基本有序“时,再对全体记录进行一次直接插入排序。
package Sort;
//希尔排序是插入排序的改良
public class ShellSort {
public static void main(String[] args) {
int [] arr={16,25,12,30,47,11,23,36,9,18,31};
sort(arr);
print(arr);
}
private static void sort(int [] arr) {
//gap设置优化
int h=1;
while(h0;gap=(gap-1)/3) {//gap:希尔排序的间距
for (int i = gap; i < arr.length; i++) {
for (int j = i; j >gap-1; j-=gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}
}
private static void swap(int [] arr,int i,int j){
int temp=0;
temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
private static void print(int [] arr) {
for (int i = 0; i
9 11 12 16 18 23 25 30 31 36 47
Process finished with exit code 0
三、冒泡排序
冒泡排序
四、快速排序
对冒泡排序的一种改进
基本思想:
通过一趟排序将待排序记录分割成独立的两部分,其中一部分的关键字均比另一部分的关键字小,则可分别对这两部分记录继续分别进行排序,以达到整个序列有序。
package Sort;
import java.util.Arrays;
//快速排序
public class QuickSort {
public static void main(String[] args) {
int[] arr={49,38,65,97,76,13,27,49};
sort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
private static void sort(int [] arr,int start,int end) {
if(start=arr[low]){
low++;
}
//用左边的数字替换右边的数字
arr[height]=arr[low];
}
arr[low]=stared;
sort(arr,start,low);
sort(arr,low+1,height);
}
}
}
[13, 27, 38, 49, 76, 97, 65, 49]
Process finished with exit code 0
五、选择排序(Selection Sort)
选择排序
六、堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
1、大顶堆举例说明:
我们对堆中的结点按层进行编号,映射到数组中就是下面这个样子:
大顶堆特点:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] // i 对应第几个节点,i从0开始编号
2、小顶堆举例说明
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] // i 对应第几个节点,i从0开始编号
一般升序采用大顶堆,降序采用小顶堆
堆排序基本思想
一、堆排序的基本思想是:
将待排序序列构造成一个大顶堆
此时,整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换,此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
二、代码示例
package Sort;
import java.util.Arrays;
/**构造大顶堆
* 1、原顺序二叉树 非叶子节点在数组中的索引i=1时;arr[i]=6 i=0时
* 4 i的右节点值比它大,交换得 : 9
* /\ 4 /\
* 6 8 /\ 6 8
* /\ 9 8 /\
* 5 9 /\ 5 4
* 5 6
*/
public class HeapSort {
public static void main(String[] args) {
int [] arr={4,6,8,5,9};
heapSort(arr);
}
//编写一个堆排序的方法
public static void heapSort(int[] arr){
int temp=0;
for(int i=arr.length/2-1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
//将堆顶元素与末尾元素进行交换,此时末尾就为最大值,将最大值全放在数组最后
//重新调整结构,使其满足堆定义,继续交换堆顶元素与当前末尾元素,反复执行调整交换步骤,使整个序列达到有序
for(int j=arr.length-1;j>0;j--) {
//交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
System.out.println("数组"+Arrays.toString(arr));
}
//将数组调整为一个大顶堆
/**
* 功能:完成将以i对应的非叶子节点的树调整成大顶堆
* 举例:int[]arr={4,6,8,5,9};=>i=1=>adjustHeap=>得到{4,9,8,5,6}
* 如果再次调整adjustHeap传入i=0,{4,9,8,5,6}=>得到{9,6,8,5,4}
* @param arr 表示要调整的数组
* @param i 表示非叶子节点在数组中的索引
* @param length 表示对多少个元素进行调整,length在逐渐减少
*/
public static void adjustHeap(int[]arr,int i,int length){
int temp=arr[i];//先取出当前元素的值,保存在临时变量中
//开始调整
//k=i*2+1;k是i节点的左子节点
for(int k=i*2+1;ktemp){//如果子节点大于父节点
arr[i]=arr[k];//把较大的值赋给当前节点
i=k;//!!!i指向k,继续循环比较
}else{
break;
}
}
//当for循环结束后,已经将以i为父结点的最大值放在了堆顶上(局部)
arr[i]=temp;//将temp的值放在调整后的位置
}
}
堆排序结果:
数组[4, 5, 6, 8, 9]
七、归并排序
定义:
又一类不同的排序方法,将两个或两个以上的有序表合并成一个新的有序表。
需要辅助空间:O(n)
整个归并需要 [log2n] 趟
时间复杂度:O(nlog2n)
缺点:归并排序占用附加存储较多, 需要另外一个与原待排序对象数组同样大小的辅助数组。
优点:归并排序是一个稳定的排序方法
思路可以推广到“多路归并”
常用于外部排序
package Sort;
//归并排序
public class MergeSort {
public static void main(String[] args) {
int [] arr={4,5,7,8,1,2,3,6};
sort(arr);
print(arr);
}
private static void sort(int [] arr) {
int mid=arr.length/2;
int[]temp=new int[arr.length];
int i=0;//标记左边数组
int j=mid+1;//标记右边数组起始点
int k=0;
while(i<=mid&&j
1 2 3 4 5 6 7 8
Process finished with exit code 0
总结
本篇文章就到这里了,希望可以给你带来一些帮助,也希望您能够多多关注脚本之家的更多内容!