【作业】{r} :自编实现K-Means聚类算法的函数,且画出每一次迭代中每组中心点的变动情况
作业要求:
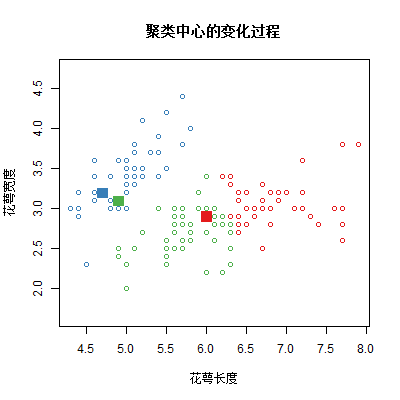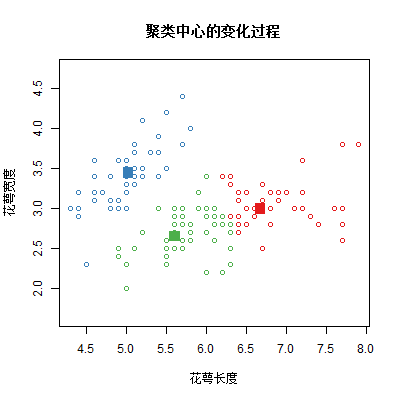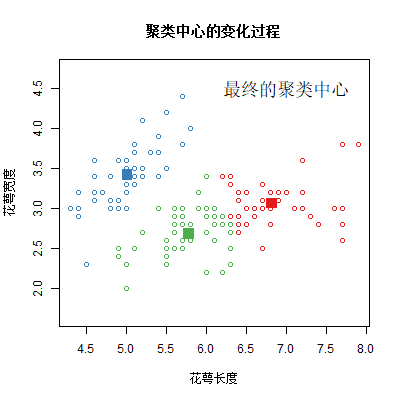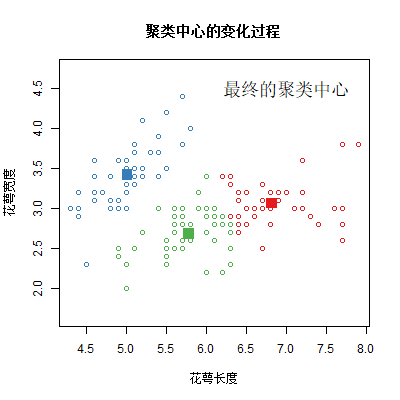
在本节中, 我们想要通过自己编写一个K-Means函数来更加深入的理解K-Means算法的流程. 并且在输出k个中心点位置和k个分组的基础上, 还想在每一次迭代中画出当前中心点的位置, 以便将这个算法动态的展示出来.
↓↓↓ 交作业点击下面链接
链接失效了
附上完整代码
(1)
# 定义函数
my_kmeans = function(data, k, err){
# 导入数据
dat = as.matrix(data)
# 选取k个初始中心
idx = sample(1:nrow(data),k)
c = matrix(NA, nrow = k, ncol = ncol(dat))
for(n in 1:k){
c[n,] = dat[idx[n],]
}
# 保存每次迭代的中心点
save = list(c)
# 迭代次数
count = 0
repeat{
# 计算每一个样本对于聚类中心的距离,保存在一个150*k的矩阵中
mat = matrix(NA, nrow = nrow(dat), ncol = k)
for(i in 1:nrow(dat)){
x = dat[i,]
for(j in 1:k){
mat[i,j] = sqrt(sum((x - c[j,])^2))
}
}
groups = apply(mat, 1,which.min)
cnew = matrix(NA, nrow = k, ncol = ncol(dat))
for(n in 1:k){
cnew[n,] = apply(dat[groups == n,], 2, mean)
}
# 终止条件
condition = c()
for(n in 1:k){
condition[n] = sqrt(sum((cnew[n,] - c[n,])^2)) < err
}
for(n in 1:k){
c[n,] = cnew[n,]
}
save = c(save,list(c))
count = count + 1
if( !(F %in% condition) )
break
}
result = list(groups,c)
names(result) = c("Groups","Cluster_centers")
return(c(result,list(save,count)))
}(2)
dat = iris[,1:2] # 数据
k = 3 # 分几类
# 引用函数
re = my_kmeans(iris[,1:2], 3, 1e-10)
# 提前设置好颜色
## install.packages("RColorBrewer")
library(RColorBrewer)
display.brewer.pal(12,"Paired")
co = brewer.pal(12,"Paired") # 配置的颜色数目不能超过k
# 动图展示聚类中心的变化过程
## install.packages("animation")
library(animation)
saveGIF(
{
for(i in c( 0:re[[4]], rep(re[[4]],5) )){ # rep这里是为了让最终的聚类中心停留更长时间
# 底图部分
plot(x=iris[,1], y=iris[,2], col=re$Groups,
xlab='花萼长度', ylab='花萼宽度', asp=1, type="n",
main="每次迭代中心点的变化")
for(j in 1:k){
points(dat[re$Groups == j,][,1:2],col=co[j])
}
# 变化部分
points(re[[3]][[i+1]][,1:2],pch=22,cex=2,
col=co[1:k],bg=co[1:k])
# 增加部分
if(i == re[[4]]){
text(7.2,4.5,labels = "聚类中心", cex=1.5)
}
}
}, interval=0.5, ani.width=400, ani.height=400, movie.name="娜可露露.gif"
)结果展示: