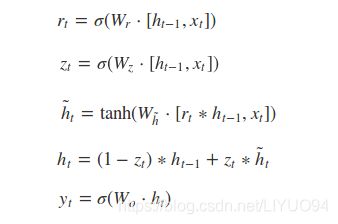GraphBind: 通过层次图神经网络学习蛋白质局部结构嵌入规则以用于识别核酸结合残基

《GraphBind: protein structural context embedded rules learned by hierarchical graph neural networks for recognizing nucleic-acid-binding residues》
作者：夏莹，春秋夏，潘晓勇，沈宏斌
单位：上海交通大学
发表时间：2021年2月12日
发表期刊：Nucleic Acids Research
paper
code and dataset

ABSTRACT

了解蛋白质和核酸之间的相互作用是了解各种生物活性和设计新药的基础。如何准确识别核酸结合残基仍然是一个具有挑战性的任务。在本文中，我们提出了一种基于端到端图神经网络的准确预测器GraphBind，用于识别蛋白质上的核酸结合残基。考虑到结合位点通常在局部三级结构上表现为高度保守的模式，我们首先根据目标残基结构上下文背景和空间领域构造图，利用层次图神经网络(HGNN)嵌入潜在的局部结构和生化特征模式，用于结合残基的识别。我们在DNA/RNA基准数据集上全面评估GraphBind。结果表明，GraphBind的性能优于最先进的方法。此外，将GraphBind扩展到其他配体结合残基预测，以验证其泛化能力。GraphBind的网络服务器可在http://www.csbio.sjtu.edu.cn/bioinf/GraphBind/.免费获得

INTRODUCTION

蛋白质和核酸之间的相互作用参与了多种生物学活动和过程，如基因复制和表达、信号转导、调节和代谢(1-3)。研究蛋白质和核酸之间的相互作用对于分析遗传物质、了解蛋白质功能和设计新药具有重要意义。为了研究分子间的相互作用，人们设计了许多实验方法，如X射线、核磁共振、激光拉曼光谱等。然而，它们通常既耗时又昂贵。开发可靠和准确的计算方法来大规模筛选识别核酸结合残基是非常有必要的(4)。

根据使用的数据类型，现有的识别核酸结合残基的计算方法一般可以分为两类：基于序列的方法和基于结构的方法。基于序列的方法，如ConSurf(5)，TargetDNA(6)，DRNApred(4)，Scriber(3)和d Target S(7)，使用序列衍生物理化特性特征。例如，在TargetDNA中，从蛋白质序列中提取蛋白质的进化保守信息和预测的溶剂可及性，并使用支持向量机从由滑动窗口策略确定的DNA结合残基的序列上下文中识别DNA结合残基(6)。基于序列的方法的优点是，它们可以仅根据其序列对任何蛋白质进行预测。然而，它们的性能可能是有限的，因为结合残基的潜在模式仅从它们的序列中并不明显，而在空间结构中是保守的(8，9)。因此，从蛋白质序列中捕获的特征可能不足以准确地表示残基。

与基于序列的方法不同，基于结构的方法的假设是，具有特定功能的结构基序通常在局部三级结构(8，9)上表现为高度保守的模式。基于结构的方法可分为以下两类：(I)基于模板的方法，如DR bind1(10)和TM-site(11)，通过结构比较为查询蛋白质寻找可靠的模板，并根据物理和化学原理推断蛋白质与核酸之间的相互作用；(ii)基于特征的机器学习方法，如Aarna(12)和NucleicNet(13)，其利用来自蛋白质结构的特征构造分类器。

功能位点通常由序列(14)以外的三级结构的局部模式决定。我们致力于用基于特征的机器学习方法从蛋白质结构中识别与核酸结合的残基。一个主要的挑战是如何嵌入关键的结构和生物物理化学特征来识别下游结合残基。以前的方法通常使用手工制作的特征来表示结构(12)。这些方法需要很强的领域知识，手工制作的特征可能无法捕获特定下游任务的蛋白质的关键信息。一些其他方法将蛋白质结构编码到三维(3D)欧几里德空间(15，16)。例如，DeepSite将蛋白质原子映射成3D体素来表示蛋白质结构(16)。然后使用3D卷积神经网络(3DCNNs)(17)基于3D体积表示(16)从其邻域中提取目标残基的抽象特征。蛋白质结构的三维体积表示有两个潜在的缺点：(1)残基的稀疏和不规则分布使残基的邻域信息难以表示；(2)难以保证在三维直角坐标系中旋转和平移的不变性。或者，Delia计算距离矩阵来表示残基对的距离关系。Delia将结构看作2D图像，使用固定大小的卷积核(18)从所有残基(19)的局部距离关系中学习模式，导致某些残基的邻域信息不完整，忽略了结构相邻残基之间传递的知识。

为了更好地捕捉蛋白质结构信息和残基之间的空间关系，用图表示蛋白质结构，节点表示残基，边根据残基之间的空间关系定义。该图表示法不仅具有旋转和平移的不变性，而且可以处理数量不断变化的残基无序邻域。最近，图神经网络(GNNs)已经成为计算生物学中处理图数据的有力工具(20)。例如，Fout等人。提出了一种基于GNN的方法，用于从蛋白质结构中对成对残基相互作用进行分类(21)。十角形使用图卷积网络(GCNS)预测不同药物组合的副作用(22)。DimiG使用半监督GCNS在交互图上推断与microRNA相关的疾病(23)。Torng和Altman提出了一个两步图-卷积(Graph-CNN)框架，用于预测药物与靶标的相互作用(24)。以上研究表明，神经网络在处理生物和化学图数据方面是有效的。

在这项研究中，我们提出了一个准确的核酸-酸结合残基预测器，GraphBind，基于结构上下文和层次图神经网络(HGNNs)构建的图。为了从蛋白质结构中提取关键的结构和生物物理化学特征的局部模式，对于每个目标残基，我们首先基于目标残基的局部环境构建一个图。初始节点特征向量包括进化保守性、二级结构信息、其他生物物理化学特征和位置嵌入。位置嵌入是根据定义结构上下文中残基的空间关系的几何知识来计算的。初始边缘特征向量也是由几何知识导出的。然后，我们构造了一个层次图神经网络来学习潜在的局部模式，用于结合残基预测。设计了边更新模块、节点更新模块和图更新模块，学习目标残基的高层几何和生物物理化学特征，并对目标残基进行固定大小的嵌入。此外，门控递归单元(25)用于堆叠多个GNN块，利用了所有块的信息，避免了梯度消失问题。实验结果表明，GraphBind在核酸结合残基预测方面具有较好的性能。此外，我们还证明了GraphBind可以扩展到其他配体结合残基的预测，具有良好的性能。

MATERIALS AND METHODS

在本节中，构建了两个基准数据集来评估GraphBind的性能。然后介绍了HGNN的图结构和体系结构。最后，对评估方案和详细的实验环境进行了简要的总结

Benchmark datasets

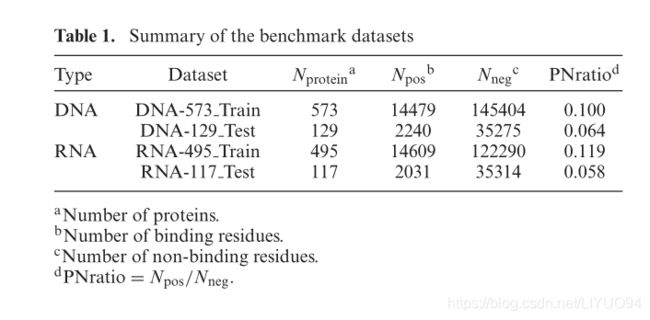
为了评估GraphBind的性能，并将其与其他方法进行公平的比较，我们从BioLiP数据库(26)中构建了两个核酸结合蛋白基准数据集，并根据发布日期将它们分为训练集和测试集。基准数据集可在http://www.csBio.sjtu.edu.cn/Bioinf/GraphBind/Datets.html上获得。

DNA/RNA结合蛋白收集自2018年12月5日发布的BioLiP数据库。这个数据库是生物上相关的配体蛋白相互作用的集合，这些相互作用在复合物中结构上被解决。如果靶残基与核酸分子之间的最小原子距离小于0.5˚A加上最近的两个原子范德华半径之和，则定义为结合残基。

BioLiP包含2018年12月5日6,342个核酸-蛋白质复合体中的48133个核酸结合位点。这些复合体分为4344个DNA-蛋白质复合体(9574个DNA结合蛋白链)、1558个RNA蛋白质复合体(7693个RNA结合蛋白链)和440个DNA-RNA-蛋白质复合体。我们排除了DNARNA-蛋白质复合物以避免混淆，因为在BioLip数据库中没有做任何注释来区分DNA或RNA结合残基。根据发布日期，2016年1月6日之前发布的蛋白质链被分配到原始训练集(6731条DNA结合蛋白链和6426条RNA结合蛋白链)，其余的蛋白质链被分配到原始测试集中(2843条DNA结合蛋白链和1267条RN绑定蛋白链)。

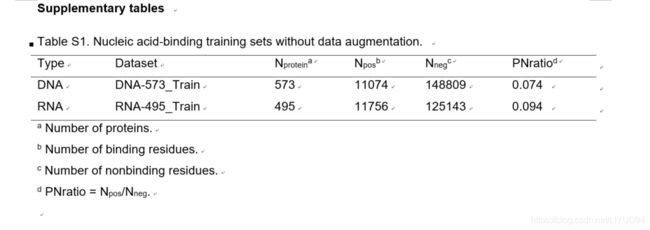
由于DNA/RNA结合残基预测存在数据不平衡问题，即DNA/RNA结合残基的数量远小于非结合残基的数量，因此我们将数据增强方法应用于原始训练集。在先前的研究(3，4，27-29)之后，我们从相似的蛋白链中转移结合注释，以增加训练集中的结合残基数量，原因如下：(I)具有相似序列和结构的蛋白质，虽然可以来自不同的生物体，但可能具有相同的生物学功能；(Ii)不同的分辨率可能导致同一蛋白质的结构略有不同。为此，我们首先应用bl2seq(30)(E值<0.001)和TM-Align(31)来评估蛋白质链对之间的序列同一性和结构相似性。其次，我们对序列同一性>0.8和TM得分>0.5的链进行聚类。第三，将同一簇中蛋白质链的注释转移到残基数量最多的链中。在转移结合注释后，我们进一步用CD-HIT(32)去除多余的蛋白质链，将训练集中的序列同一性降低到30%以下。最后，我们得到了573条DNA结合蛋白链和495条RNA结合蛋白链作为训练集。数据增强使DNA结合残基和RNA结合残基分别增加了30.7%和24.3%。去除从原始DNA/RNA结合测试集合到DNA/RNA结合训练集合中的任意链的蛋白质链，所述原始DNA/RNA结合测试集合具有CD-HIT(32)测量的超过30%的序列同一性。最后，我们分别获得129个DNA结合蛋白和117个RNA结合蛋白作为DNA和RNA结合测试集。表1汇总了数据集的详细信息(未增加数据的训练集见补充表S1)。

Graph construction based on structural contexts

提取了基于序列和基于结构的多种特征，包括伪位置特征、残基原子特征、二级结构特征和进化会话特征。然后，使用3D空间中定义的滑动球来提取以残基为中心的目标残基的结构上下文。基于残基在结构上下文中的伪位置计算的邻接矩阵被用来构造图。此外，在节点和边缘特征向量中嵌入了几何知识和生物物理化学特征。图1显示了图构建的管道。

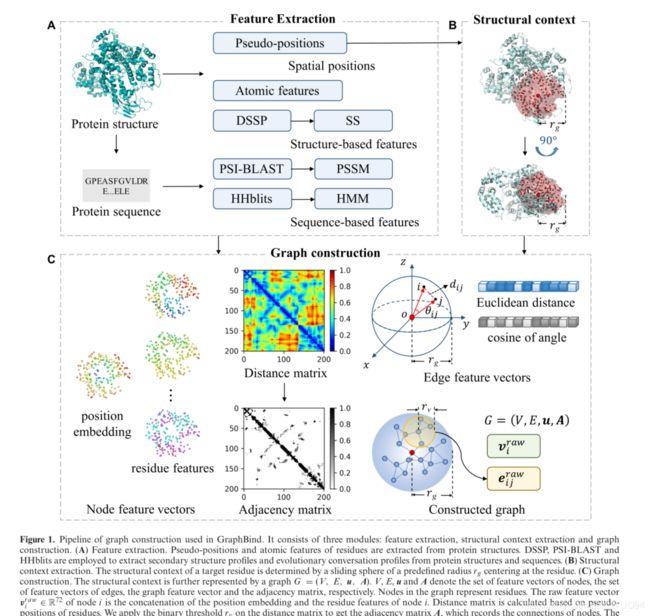
图1.GraphBind中使用的图构造管道。它包括三个模块：特征提取、结构上下文提取和图构造。(A)特征提取。从蛋白质结构中提取残基的伪位置和原子特征。利用DSSP、PSI-BLAST和HHblits从蛋白质结构和序列中提取二级结构特征和进化会话特征。(B)结构上下文提取。目标残基的结构上下文由以残基为中心的预定半径的滑动球体确定。(c )图构造。结构上下文进一步由图$G=(V,E,u,A)$表示。V、E、u和A分别表示节点的特征向量集合、边的特征向量集合、图特征向量和邻接矩阵。图中的节点表示残基。节点I的原始特征向量$V_i^{raw}\in {\mathbb{R}}^{72}$是节点I的位置嵌入和残基特征的拼接，距离矩阵是根据残基的伪位计算的。在距离矩阵上应用二进制阈值$r_v$，得到记录节点连接的邻接矩阵A。边ij的原始特征向量$e_{ij}^{raw}\in {\mathbb{R}}^2$分别由两个相邻结点之间的欧几里得距离和两个向量之间从球心到两个相邻结点的夹角θij的余弦编码

特征提取。推导出四种类型的残基水平特征如下：

第一个是伪位置。包括残基的主链和侧链原子的残基的质心被表示为该残基的伪位置，因为蛋白质和核酸之间的相互作用可以发生在主链和侧链原子(33)上。

二是残基的原子特征。对于残基，我们提取了属于残基(不包括氢原子)的每个原子的以下七种特征：原子质量、B因子、是否为残基侧链原子、电荷、与其键合的氢原子数、是否在环中以及原子的范德华半径。残基的原始原子特征表示为${\left\{f_{s,t}\right\}}_s=1,\dots ,7,t=1,\dots ,N_a$，$\{f_{s,t}\}$代表第t-th原子的某些特征，$N_a$代表属于残基的原子数。由于不同的残基可能具有不同的原子数，我们将所有原子的某物特征平均为残基的加工的某物原子特征xs，这导致对于每个残基$\{X_s{\}}_s$=1，…，7：

$$x_s=\frac{1}{N_a}\left(\sum _{t=1}^{t=N_a}{f}_{s,t}\right)$$

最后，我们为含有$L$个残基的查询蛋白质生成一个$L\times 7$的原子特征矩阵。三是二级结构剖面。DSSP(34，35)生成$L\times 14$矩阵形式的二级结构轮廓，包括1列渣油暴露表面，5列键角和扭角，8列8种状态的单热编码二级结构。二级结构的8种状态包括B(residue in isolated β-bridge),E(extended strand, participates in β-ladder), G(310-helix),H(α-helix), I(π-helix), S(bend), T(H-bonded turn) 和其他.

最后是两种进化的对话模式。
(1)PSI-BLAST配置文件。比对工具PSI-BLAST使用启发式算法和动态规划来搜索NCBI的非冗余数据库(NR)，以查找具有三次迭代且$E_{value}<10^{-3}$(36)的同源序列。生成的特定位置评分矩阵(PSSM)的大小为$L\times 20$。PSSM中的每个元素$x$通过Sigmoid函数归一化到范围[0，1]：
$$\bar{x}=\frac{1}{1+e^{-x}}$$

(2)HHblits剖面。基于隐马尔可夫模型(HMM)的HHblits被用于针对具有默认参数的uniclust30数据库进行搜索，以生成查询序列的HMM矩阵(37)。HMM矩阵的大小为$L\times 30$。HMM矩阵由同源序列中20种氨基酸的20列观测频率、7列转换频率和3列局部差异组成。每个分数都转换为范围[0，1]：

$$\bar{x}=\frac{1}{10000}$$
PSI-BLAST和HHblits配置文件是互补的，因为它们的后端算法和搜索的数据库是不同的，这在我们随后的实验中得到了证实。

综上所述，对于一个查询蛋白质，我们得到了大小为$L\times 3$的伪位矩阵和大小为$L\times 71$的特征矩阵。对于特征矩阵中的每一列，执行最小-最大归一化以将该值线性归一化为[0，1]：

$$\bar{x}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

其中，$x_{min}和x_{max}$值分别是训练集中该特征的最小值和最大值

结构化上下文提取。根据三级结构中残基的伪位，一个球体沿着多肽链滑动，以获得每个残基的结构上下文。对于目标残基，结构上下文被定义为以该残基为中心半径为$r_g$的球体。球体中的所有残基及其几何知识形成了目标残基的局部结构上下文。与蛋白质的整体结构相比，结合位点通常更多地与其局部结构环境的几何和生物物理化学性质有关(8-9，15)。

图构造。在此步骤中，残基的结构上下文进一步表示为图。图$G=(V，E，u，A)$，其中$V={\left\{{\mathbf{v}}_i\right\}}_{i=1,\dots ,N_v}$和${\mathbf{v}}_i\in {\mathbb{R}}^{D_v}$分别表示$N_v$节点的特征向量集合和节点i的特征向量。添加$N_v\times N_v$形状的邻接矩阵。$E=\left\{{\mathbf{e}}_{ij}\mid {\mathbf{A}}_{ij}=1\right\}$表示$N_e$的特征向量集合。${\mathbf{e}}_{\mathbf{i}\mathbf{j}}\in {\mathbb{R}}^{D_e}$表示节点i和j之间的边ij的特征向量。${\mathbf{e}}_{ij}\in E$ if ${\mathbf{A}}_{ij}=1,{\mathbf{e}}_{ij}\notin E$ if ${\mathbf{A}}_{ij}=0$。U代表图特征向量。在图中，残基表示为节点。由相应残基的伪位置定义的第i个节点$P_i$的位置。靶残基周围的残基可能形成特定的局部几何图案，这对结合残基的识别是有用的。基于这一观察，我们使用位置嵌入来表示目标残基与其每个上下文残基之间的位置关系，因为它包含目标残基周围的局部几何知识。将节点i的位置嵌入定义为节点$ii$与球心之间的归一化欧几里德距离，
$$P{E}_i=\frac{1}{r_g}\left|{\mathbf{p}}_o{p}_i\right|$$

其中$P_o和P_i$分别表示球心和节点i的位置，${\mathbf{p}}_o{\mathbf{p}}_i$ 是从$P_o$到$P_i$的向量。节点i的原始特征向量${\mathbf{v}}_i^{\text{raw }}\in {\mathbb{R}}^{72}$是嵌入位置$P{E}_i$和节点的71个残基特征的连接。原始节点特征向量集合表示为$V^{raw}=\{v_i^{raw}{\}}_{i=1，...，N_v}$。
然后，构造了大小为$N_v\times N_v$的距离矩阵D。元素$D_{ij}$是节点i和节点j之间的欧几里得距离：
$${\mathbf{D}}_{ij}=\left|{\mathbf{p}}_i{\mathbf{p}}_j\right|$$
我们使用阈值$r_v$ 在D来获得邻接矩阵A，
$${\mathbf{A}}_{ij}=\{\begin{array}{l}1,\text{ if }{\mathbf{D}}_{ij}<r_v\\ 0,\text{ if }{\mathbf{D}}_{ij}\ge r_v\end{array}$$
基于验证集选择的$r_v$值。边ij的原始特征向量被表示为${\mathbf{e}}_{ij}^{raw}\in {\mathbb{R}}^2$，其由两个与几何知识相关的属性组成：(I)节点i和节点j的欧几里德距离${\mathbf{D}}_{ij}$,以及(ii)两个向量${\theta }_{ij}$和 ${\mathbf{p}}_o{\mathbf{p}}_i$和${\mathbf{p}}_o{\mathbf{p}}_j$之间的角度的余弦，这两个向量分别是从球心到节点i和节点j的向量：

$$\cos \left({\theta }_{ij}\right)=\frac{{\mathbf{p}}_o{\mathbf{p}}_i\cdot {\mathbf{p}}_o{\mathbf{p}}_j}{\left|{\mathbf{p}}_o{\mathbf{p}}_i\right|\left|{\mathbf{p}}_o{\mathbf{p}}_j\right|}$$

其中$\cdot$表示点积。$e_{ij}^{raw}$也归一化为[0，1]。原始边缘特征向量集合表示为$E^{raw}=\{e_{ij}^{raw}|Aij=1\}$。值得注意的是，节点和边的所有位置相关特征都是根据节点之间的相对距离来定义的。因此，GraphBind对于旋转和平移是不变的。

Hierarchical graph neural networks

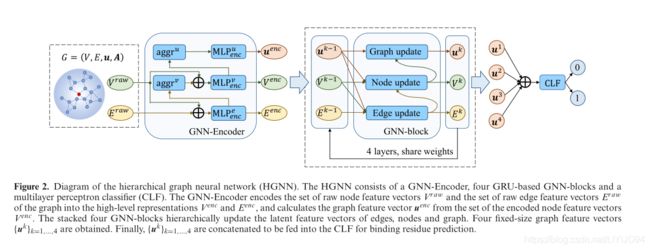
在利用几何知识和生物物理化学特征构建每个残基的图之后，设计了一个层次图神经网络(HGNN)，将图嵌入到固定大小的图级潜在表示中，用于下游预测。HGNN由三个模块组成。(I)图神经网络编码器(GNNEncode)。它被设计用于将原始边和节点特征向量集合编码成高层表示，并从编码后的节点特征向量集合计算图特征向量。(ii)基于门循环单元的图神经网络块(GNN块)。通过层叠4个GNN块来扩大感受域的范围，并分层更新边、节点和图的潜在特征向量。每个GNN块将结构上下文嵌入到固定大小的图特征向量中。(Iii)多层感知器分类器(CLF)。利用上述四个图特征向量中的串联向量对结合残基进行分类。HGNN的示意图如图2所示。
在这里，我们首先介绍两种基本操作，多层感知(MLP)和门控递归单元(GRU)。
(1)MLP。MLP是公式(9)中定义的逐点非线性变换。由两个线性层和一个整流线性单元(REU)(38)组成：
$$\mathrm{MLP}(\mathbf{X})={\mathbf{W}}_2\max \left(0,{\mathbf{W}}_1\mathbf{X}+{\mathbf{b}}_1\right)+{\mathbf{b}}_2$$

(2)GRU(25)。GRU广泛应用于文本序列的自然语言处理中。它不会随着时间的推移删除先前的信息，而是保留相关信息，并通过对输入和隐藏状态进行非线性加权来推断输出，将其传递给下一个单元。GRU充分利用了所有单元的信息，避免了梯度消失。对于每个时间步长t，基于输入$X^t$和前一隐藏状态$h^{t-1}$，GRU的输出通过以下方式计算：
$$\begin{array}{c}{r}_t=\sigma \left({\mathbf{W}}_r{\mathbf{X}}^t+{\mathbf{U}}_r{\mathbf{h}}^{t-1}\right)\\ z_t=\sigma \left({\mathbf{W}}_z{\mathbf{X}}^t+{\mathbf{U}}_z{\mathbf{h}}^{t-1}\right)\\ {\tilde{\mathbf{h}}}^t=\tanh \left({\mathbf{W}}_{\tilde{h}}{\mathbf{X}}^t+{\mathbf{U}}_{\tilde{h}}\left(r_t\cdot {\mathbf{h}}^{t-1}\right)\right)\\ {\mathbf{h}}^t=z_t{\mathbf{h}}^{t-1}+\left(1-z_t\right){\tilde{\mathbf{h}}}^t\end{array}$$
其中 $\sigma$ 是S型激活函数， $\cdot$表示点积。 $r_t$是复位门，它确定可以传送多少来自先前隐藏状态${\mathbf{h}}^{t-1}$的信息。$z_t$是更新门，其确定先前隐藏状态 ${\mathbf{h}}^{t-1}$和新隐藏状态${\tilde{\mathbf{h}}}^t$ 在更新的隐藏状态${\mathbf{h}}^t$中的比例(25)。

图2.层次图神经网络(HGNN)示意图。HGNN由GNN编码器、四个基于GRU的GNN块和多层感知器分类器(CLF)组成。GNN编码器将图形的原始节点特征向量集合$V^{raw}$原始边缘特征向量$E^{raw}$编码成高级表示$V^{enc}$ 和 $E^{enc}$，并从编码的节点特征向量集合$V^{enc}$计算图形特征向量$u^{enc}$。层叠的四个GNN块分层更新边、节点和图的潜在特征向量。得到了4个固定大小的图特征向量$u^k{=}_{1，\dots ，4}$。最后，将$u^k{=}_{1，\dots ，4}$连接起来，送入CLF进行结合残基预测。

GNN-编码器。GNN编码器将原始节点特征向量集合$V^{raw}$和原始边缘特征向量集合$E^{raw}$编码成节点 $V^{enc}={\left\{{\mathbf{v}}_i^{enc}\right\}}_{i=1,\dots ,N_v}$, edges $E^{enc}=\left\{{\mathbf{e}}_{ij}^{enc}\mid {\mathbf{A}}_{ij}=1\right\}$和图的高级表示${\mathbf{u}}^{enc}.{\mathbf{v}}_i^{enc}\in {\mathbb{R}}^{D_v},{\mathbf{e}}_{ij}^{enc}\in {\mathbb{R}}^{D_e}$ 。

首先，根据原始边缘特征向量$e_{ij}^{raw}$和原始节点特征向量$v_i^{raw}$和$v_j^{raw}$计算编码边特征向量$e_i^{enc}$：
$${\mathbf{e}}_{ij}^{enc}={\mathrm{M}\mathrm{L}\mathrm{P}}_{enc}^e\left(\left[{\mathbf{e}}_{ij}^{\text{raw }};{\mathbf{v}}_i^{\text{raw }};{\mathbf{v}}_j^{raw}\right]\right)$$
其中${\mathrm{M}\mathrm{L}\mathrm{P}}_{enc}^e$ 是执行非线性变换的MLP运算， $\left[{\mathbf{e}}_{ij}^{\text{raw }};{\mathbf{v}}_i^{\text{raw }};{\mathbf{v}}_j^{raw}\right]$表示${\mathbf{e}}_{ij}^{\text{raw }},{\mathbf{v}}_i^{\text{raw }}$ 和 ${\mathbf{v}}_j^{\text{raw }}$.的串联。

接下来，根据原始节点特征向量$v_i^{raw}$和其相邻边的上述更新的特征向量的总和来更新节点特征向量${\mathbf{v}}_i^{enc}$ ：
$${\mathbf{v}}_i^{enc}={\mathrm{M}\mathrm{L}\mathrm{P}}_{enc}^v\left(\left[{\mathbf{v}}_i^{raw};\sum _{j\in N\left(v_i\right)}{\mathbf{e}}_{ij}^{enc}\right]\right)$$
其中$N\left(v_i\right)$是节点i的邻居集合，并且${\mathrm{M}\mathrm{L}\mathrm{P}}_{\text{enc }}^v$ 是执行非线性变换的MLP运算。

最后，对该图中编码后的节点特征向量集合之和进行非线性变换，得到图特征向量${\mathbf{u}}^{\text{enc }}$ ：
$${\mathbf{u}}^{enc}={\mathrm{MLP}}_{enc}^u\left(\sum _{enc}^{N_v}{v}_i^{enc}\right)$$

其中${\mathrm{M}\mathrm{L}\mathrm{P}}_{\text{enc }}^v$是执行非线性变换的MLP运算。

堆叠多个GNN块。与CNN类似，可通过堆叠多个GNN块来扩展感受野。因此，远程边或节点可以相互影响，直到它们的潜在表示达到稳定(39)。GNN块按顺序更新边、节点和图特征向量，如图3所示。

(1)边缘更新。我们首先计算k层中间边缘特征向量$e_{ij}^{k^{\prime }}$，其采用前一层的边缘特征向量$e_{ij}^{k-1}$,两个节点特征向量${\mathbf{v}}_i^{k-1}$和${\mathbf{v}}_j^{k-1}$,以及图特征向量$u^{k-1}$的串联为输入。将输入到非线性变换MLP ${}^e$ 中，得到中间输出${\mathbf{e}}_{ij}^{k^{\prime }}$和GRU ${}^e$ 进行非线性加权变换。层k的更新后的边缘特征向量 ${\mathbf{e}}_{ij}^k$导出如下：
$$\begin{array}{c}{\mathbf{e}}_{ij}^{k^{\prime }}={\mathbf{M}\mathbf{L}\mathbf{P}}^e\left(\left[{\mathbf{e}}_{ij}^{k-1};{\mathbf{v}}_i^{k-1};{\mathbf{v}}_j^{k-1};{\mathbf{u}}^{k-1}\right]\right)\\ {\mathbf{e}}_{ij}^k={\mathrm{G}\mathrm{R}\mathrm{U}}^e\left({\mathbf{e}}_{ij}^{k^{\prime }},{\mathbf{e}}_{ij}^{k-1}\right)\end{array}$$

(2)节点更新。我们将节点i的相邻边的更新特征向量聚合为其相邻边特征向量。中间输出${\mathbf{v}}_i^{k^{\prime }}$由其邻边特征向量、 节点特征向量${\mathbf{u}}^{k-1}$和图特征向量$u^{k-1}$连接起来，对$ML{P}^v$进行非线性变换，然后计算GRU ${}^v$ 权重${\mathbf{v}}_i^{k^{\prime }}$和${\mathbf{v}}_i^{k-1}$以获得更新的节点特征向量${\mathbf{v}}_i^k$：

$$\begin{array}{c}{\mathbf{v}}_i^{k^{\prime }}={\mathrm{M}\mathrm{L}\mathrm{P}}^v\left(\left[{\mathbf{v}}_i^{k-1};\sum _{j\in N\left(v_i\right)}{\mathbf{e}}_{ij}^k;{\mathbf{u}}^{k-1}\right]\right)\\ {\mathbf{v}}_i^k={\mathrm{G}\mathrm{R}\mathrm{U}}^v\left({\mathbf{v}}_i^{k^{\prime }},{\mathbf{v}}_i^{k-1}\right)\end{array}$$
(3)图更新。节点特征向量集合的和与前一层的图特征向量${\mathbf{u}}^{k-1}$ 连接为输入，其被馈送到非线性变换${\mathrm{M}\mathrm{L}\mathrm{P}}^u$，以计算中间图特征向量${\mathbf{u}}^{k^{\prime }}$然后，使用${\mathrm{G}\mathrm{R}\mathrm{U}}^u$更新图特征向量${\mathbf{u}}^k$。$$\begin{array}{c}{\mathbf{u}}^{k^{\prime }}={\mathrm{MLP}}^u\left(\left[\sum _{i=1}^{N_v}{\mathbf{v}}_i^k;{\mathbf{u}}^{k-1}\right]\right)\\ {\mathbf{u}}^k={\mathrm{G}\mathrm{R}\mathrm{U}}^u\left({\mathbf{u}}^{k^{\prime }},{\mathbf{u}}^{k-1}\right)\end{array}$$

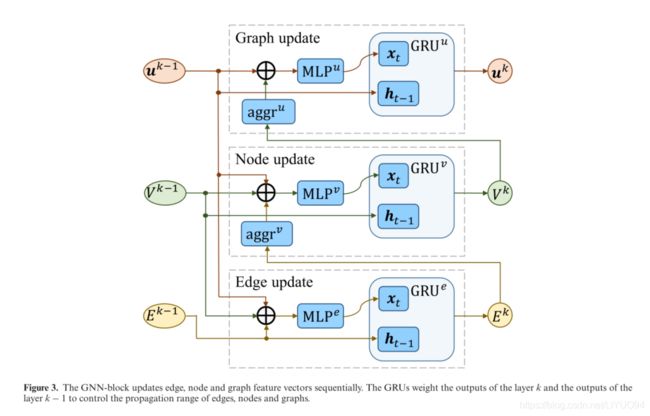
图3.GNN块依次更新边、节点和图特征向量。GRU加权第k层的输出和第k层−1的输出，以控制边、节点和图的传播范围。

多层感知器分类器。在GraphBind中，从四个GNN块中获得四个图特征向量。我们将它们连接起来作为目标残基的最终表示，原因如下：(1)由于图结构的局部多样性(40)，深层GNN的性能可能会降低；(2)每层的反向传播路径变短，这会加速模型的收敛。然后，将串联的图特征向量馈入多层感知器分类器，以获得作为结合残基ˆy的概率：

$$\hat{y}=\mathrm{softmax}\left(W_2\max \left(0,W_1\left[{\mathbf{u}}^1;\dots ;{\mathbf{u}}^K\right]+{\mathbf{b}}_1\right)+{\mathbf{b}}_2\right)$$
其中softmax $\left(x_i\right)=e^{x_i}/\left(1+{\sum }_j{e}^{x_j}\right),K=4,{\mathbf{u}}^k\in {\mathbb{R}}^{D_u},k=$
$[1,\dots ,K],W_1\in {\mathbb{R}}^{256\times \left(K{D}_u\right)},{\mathbf{b}}_1\in {\mathbb{R}}^{256},{\mathbf{W}}_2\in {\mathbb{R}}^{2\times 256}$ ,
${\mathbf{b}}_2\in {\mathbb{R}}^2.$。

不是使用默认阈值0.5来将连续值ˆy二进制化为结合或非结合残基类别，而是通过最大化每个基准数据集的验证集合上的mcc来确定最佳阈值。

Baseline and state-of-the-art methods

在本研究中，我们对GraphBind和两种方法进行了比较。(1)设计了几何不可知基线方法biLSTMClf，展示了几何知识和HGNN在GraphBind中的优势。(2)比较了现有的核酸结合残基预测方法，验证了GraphBind的有效性。

几何不可知基线方法biLSTMClf。如图4所示，biLSTMClf使用与GraphBind相同的来自蛋白质序列和结构的残基特征来将蛋白质表示为L×71矩阵，其中L代表序列的长度。对称滑动窗口(6，41-42)是用来控制序列上下文而不是靶残基的结构上下文。因此，目标残差被表示为$w_s\times 71$矩阵，其中$w_s$代表滑动窗口的大小。在获得目标残基的初始特征后，采用两层双向长短期记忆网络(BiLSTM)提取残基的潜在表征。然后，使用多层感知器分类器(CLF)来预测结合概率，该分类器也是GraphBind中的分类器。BiLSTMClf是一个几何不可知的基线，它用于评估几何知识是否是结合残基预测所必需的，以及GraphBind是否能从几何知识中学习信息丰富的潜在嵌入。

最先进的方法。为了验证GraphBind的有效性，我们将其与基于深度学习的方法、基于浅层机器学习的方法、基于模板的方法和基于共识的方法进行了比较：

(1)TargetDNA：一种基于序列的DNA结合残基预测方法。它将进化信息和预测的二级结构剖面作为输入，并使用多个支持向量机，其中Boosting作为分类器(6)。

(2)TargetS: 一种基于序列的配体结合残基预测方法，以进化信息、预测的二级结构轮廓和配体特异性倾向为输入，采用AdaBoost算法作为分类器(7)。

(3)NucBind：一种普遍适用的核酸结合残基预测方法。NucBind融合了基于序列的方法SVMnuc和共识方法Coach-D(42，43)。
(4)DNAPred：一种基于序列的DNA结合残基预测方法。DNAPred提出了一种两阶段不平衡学习算法，以减少数据不平衡问题对集成技术的影响(44)。

(5)RNABindRPlus：一种普遍适用的RNA结合残基预测方法。RNABindRPlus将来自基于序列同源性的方法的输出与来自SVM分类器(45)的输出相结合。

(6)NucleicNet：一种预测蛋白质表面RNA结合偏好的基于结构的深度学习方法。NucleicNet分析蛋白质表面网格点的物理化学性质，并以深度残差网络作为分类器。残基的结合分数由其最近的30个网格点的分数平均(13)。

(7)AARNA：一种基于序列和结构的RNA结合残基预测人工神经网络分类器。Aarna使用结构描述符拉普拉斯范数来测量不同长度尺度上的表面凸度/凹度(12)。

(8)DNABind：一种通用的DNA结合残基预测方法。DNABind集成了基于序列的支持向量机分类器、基于结构的支持向量机分类器和基于模板的方法。DNABind提取了度、贴近度、介数和聚类系数四个拓扑特征来表示几何知识(46)。

Evaluation measureme

为了评估GraphBind和其他方法的性能，我们报告了以下五个指标。二进制输出的四个度量(查全率(REC)、查准率(PRE)、F1得分(F1)和马修斯相关系数(MCC)计算如下：

$$\begin{array}{c}\mathrm{Rec}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}\\ \text{ Pre }=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}\\ \mathrm{F}1=\frac{2\cdot \mathrm{R}\mathrm{e}\mathrm{c}\cdot \mathrm{P}\mathrm{r}\mathrm{e}}{\mathrm{R}\mathrm{e}\mathrm{c}+\mathrm{P}\mathrm{r}\mathrm{e}}\\ \mathrm{M}\mathrm{C}\mathrm{C}=\frac{\mathrm{T}\mathrm{P}\cdot \mathrm{T}\mathrm{N}-\mathrm{F}\mathrm{N}\cdot \mathrm{F}\mathrm{P}}{\sqrt{(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N})(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P})(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N})(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P})}}\end{array}$$
其中TP、FP、TN和FN是真阳性(正确预测为结合残基的样本数量)、假阳性(错误预测为结合残基的样本数量)、真阴性(正确预测为非结合残基的样本数量)和假阴性(错误预测为非结合残基的样本数量)的缩写。召回衡量被正确预测为结合残基的真实结合残基的比例。精密度测量真实结合残基在预测结合残基中的比例。F1和MCC是由多个指标计算得出的，是正负样本比不平衡时的客观指标。

此外，我们报告了接收者操作员特征(ROC)曲线下的面积来评估预测分数。ROC是在概率的整个不同阈值范围内的真阳性比与假阳性比的图曲线图。在这五个指标中，F1、MCC和AUC是总体指标，特别是在测试集不平衡的情况下。所有报告的指标都是方法重复运行10次的平均值。

Significance test

进行显著性检验以调查MCC和AUC的改善是否是由于模型性能的噪声估计所致。与之前研究(4，42)中使用的程序类似，我们随机抽取70%的测试集，并计算表现最好的方法和其他方法的MCC和AUC，重复10次。安德森-达林检验用于评估测量是否正常。如果测量正常，则配对的T检验用于计算测量的显著性。否则，应用Wilcoxon秩和检验。如果所获得的P值<0.05，则认为给定的两种方法之间的差异在统计学上是显著的。

Experimental settings

表1中原始训练集的20%的蛋白质用于构建验证集$V_{val}$，剩余的蛋白链用于构建训练集$V_{tr}$。我们还使用CD-HIT来确保验证集和训练集之间的序列相似度小于30%。在训练过程中，使用网格搜索来寻找最优超参数。

我们使用β1=0.9，β2=0.999，ε=$10^{-8}$，学习率为$5\times 10^{-5}$的ADAM优化器对交叉熵损失进行模型优化，结果如下：$$\mathrm{Loss}=\sum _{v_i\in V_{tr}}\left(y_i\ln y_i+\left(1-y_i\right)\ln \left(1-y_i\right)\right)$$
其中$y_i$残基的标签，$y_i$是对应$y_i$的预测概率。

以$P_{drop}=0.5$的速率对每个MLP模块应用丢弃(47)，以避免过拟合。为了加快收敛速度和提高泛化性能，在MLP的每一卷积层上都采用了批归一化.

RESULTS

在本节中，我们首先进行烧蚀研究，以调查不同设置对GraphBind性能的影响。然后，我们在核酸-酸结合基准数据集上将GraphBind与几何不可知的基线和最新的方法进行了比较，以展示所提出的基于结构上下文的图表示和HGNN的优势。此外，我们还研究了不同特性的贡献、通过传输绑定注释进行数据扩充的影响，以及它们在使用来自序列的预测结构时对GraphBind的影响。

Ablation studies on GraphBind

为了研究不同设置的GraphBind对GraphBind的贡献，我们在DNA573Train的验证集上对不同设置的GraphBind进行了烧蚀研究。这些结果载列於表二。

如表2所示，实验A-D评估了不同设置对图构建的贡献。如实验A所示，由残基质心表示的伪位置比由α-C原子表示的伪位置产生更高的性能，并且获得了由残基侧链质心表示的相似结果。结果表明，残基或残基侧链的质心与结合位点的相关性高于单一主干α-C原子。实验B表明，在更新图特征向量时，位置嵌入可以用来区分节点，因此采用每个节点与球心的相对距离作为位置嵌入是有利的。如实验C和D所示，较小的结构上下文半径和较少的边限制了网络的接受范围，从而导致较差的性能。然而，较大的结构上下文半径和更多的边也不会对性能带来好处，而是需要更长的训练时间。

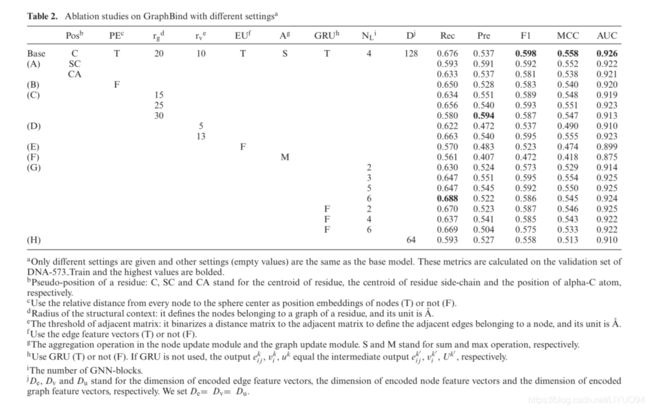
我们还在GraphBind中测试了H.
GNN的不同网络组件。在实验E中，忽略了边缘特征向量，并计算了EQ。(15)和(19)由等商数取代。(29)和(30)

$$\begin{array}{c}{\mathbf{v}}_i^{enc}={\mathrm{M}\mathrm{L}\mathrm{P}}_{enc}^v\left(\left[{\mathbf{v}}_i^{\text{raw }};\sum _{j\in N\left(v_i\right)}{\mathbf{v}}_j^{\text{raw }}\right]\right)\\ {\mathbf{v}}_i^{k^{\prime }}={\mathrm{M}\mathrm{L}\mathrm{P}}^v\left(\left[{\mathbf{v}}_i^{k-1};\sum _{j\in N\left(v_i\right)}{\mathbf{v}}_j^{k-1};{\mathbf{u}}^{k-1}\right]\right)\end{array}$$

实验E的性能下降说明了将边缘特征向量集成到节点更新模块中的重要性以及几何知识的重要性。实验F使用最大聚合而不是总和聚合，导致性能较低。这可能是因为最大池操作只记录了最大值，而丢失了其他节点的信息。如实验G所示，我们研究了GNN块数量的影响，并对这些GNN块进行了GR-U操作或不进行GR-U操作的堆叠。如果不使用GR U，则删除$GR{U}^e$、${\mathrm{G}\mathrm{R}\mathrm{U}}^v$和${\mathrm{G}\mathrm{R}\mathrm{U}}^u$，并将输出${\mathbf{e}}_{ij}^k,{\mathbf{v}}_i^k,{\mathbf{u}}^k$设置为中间输出${\mathbf{e}}_{ij}^{k^{\prime }},{\mathbf{v}}_i^{k^{\prime }},{\mathbf{u}}^{k^{\prime }}$。结果表明，仅堆叠两个GNN块会导致性能下降，因为堆叠较少GNN的接受范围是有限的。添加更多没有GR U的GNN块也会导致较差的性能。结果表明，较深的GNN可以从GRU中受益，因为它利用了所有块的信息。实验H表明，对边、节点和图设置128的隐含表示可以提取更多的区分特征，并获得更好的性能。

GraphBind is superior to geometric-agnostic biLSTMClf

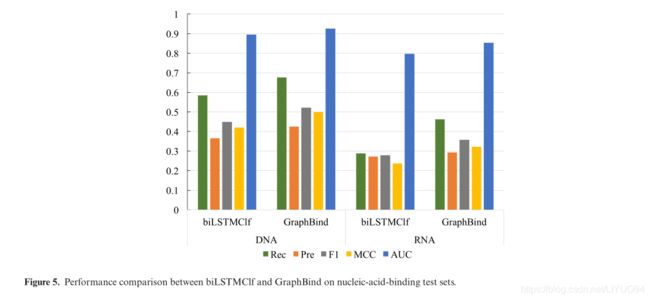
我们根据几何不可知的基线方法biLSTMClf对GraphBind进行基准测试。这两种方法共享相同的训练集、验证集和测试集。BiLSTMClf和GraphBind的性能比较如图5所示(有关详细信息，请参见补充表S2)。与biLSTMClf相比，GraphBind的F1-Score、MCC和AUC值分别高出0.072(0.078)、0.079(0.084)和0.031(0.056)。从比较中可以得出两个观察结果。首先，几何知识是完成DNA/RNA结合残基识别任务所必需的。其次，GraphBind比biLSTMClf更有效地学习目标残基周围局部模式的潜在嵌入，因为GraphBind可以从几何知识和生物物理化学特征中以端到端的方式提取局部结构的模式。

Comparison with state-of-the-art methods on benchmark sets

对于纯粹基于序列的方法(即TargetDNA、Targets、DNAPred和RNABindRPlus)，我们将测试集的蛋白质序列上传到它们的网络服务器上。对于以结构为输入的方法，我们将测试集的PDB文件(49)上传到它们的网络服务器或独立软件。

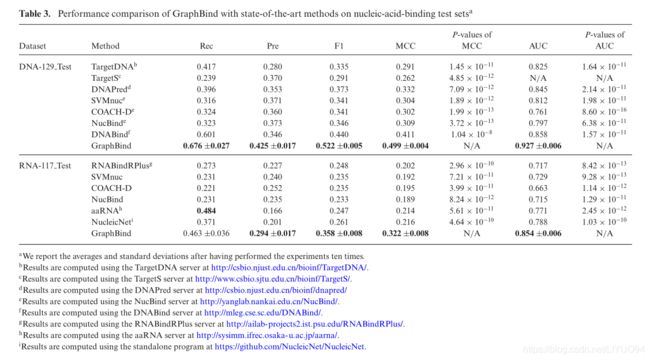
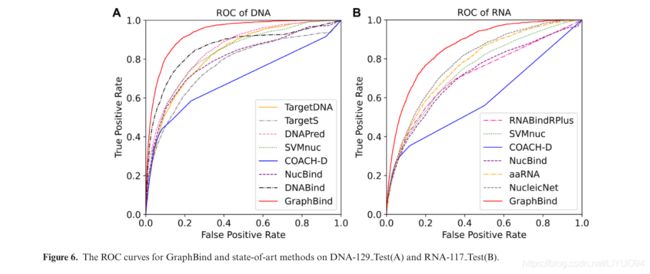
表3报告了GraphBind与最新方法在核酸结合测试集上的性能比较，ROC曲线如图6所示。如表3所示，GraphBind产生了更好的-比最先进的方法更好的性能。GraphBind的F1值、MCC和AUC值分别比第二高值高0.082(0.097)、0.088(0.106)和0.069(0.066)，分别相对提高18.6%(37.2%)、21.4%(49.1%)和8%(8.4%)。基于结构的方法(DNABind、Aarna、NucleicNet和GraphBind)的MCC一般高于基于序列的方法(TargetDNA、DNAPred、Targets、RNABindRPlus和SVMnuc)，这表明结构信息的重要性。基于模板的方法COACHD的较低AUC可能是因为模板和查询之间的相似性不够高，导致查询(42)的许多零分。GraphBind比DNABind和Aarna的优越性证明了基于结构上下文的图表示比手工制作的结构描述符更适合于表示残基的局部结构信息来识别结合残基。此外，与NucleicNet相比，GraphBind的优势表明GraphBind中的HGNN比NucleicNet中的二维图像表示中的CNN能够捕捉到更多重要的几何和生物物理化学特征。结果表明，与NucleicNet中的二维图像表示相比，GraphBind中的HGNN能够捕捉到更多重要的几何和生物物理化学特征。此外，显著性检验是在GraphBind和其他方法之间进行比较，结果表明MCC和AUC的改善在统计学上是显著的。图6A和图6B中所示的ROC曲线也验证了GraphBind的有效性。此外，我们独立计算了每条蛋白链的MCC，并在补充图S1中绘制了次佳DNA结合预测因子DNABind、次佳RNAbinding预测因子NucleicNet和GraphBind的MCC分布，这也验证了GraphBind的性能。

Case studies

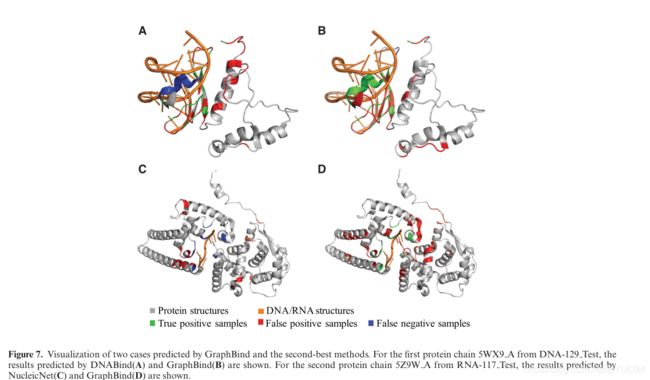
在本节中，我们将从GraphBind预测的测试集中可视化两个案例，以及分别针对DNA结合蛋白和RNA结合蛋白的次佳方法DNABind和NucleicNet。我们分别在DNA-129测试和RNA-117测试上选择了两个MCC接近整体MCC的案例(如表3所示)。一个是DNA结合蛋白5WX9A，另一个是RNA结合蛋白5Z9WA。

DNA结合蛋白5WX9A有131个残基，其中21个是结合残基(图7A和B)。GraphBind目前预测了20个真结合残基和32个假阳性残基。对于该蛋白质，GraphBind的REC=0.952，Pre=0.385，F1=0.548，mCC=0.496，AUC=0.945。在这种情况下，DNA结合预测只有14个真结合残基和32个假阳性残基，达到Rec=0.667，Pre=0.304，F1=0.418，mcc=0.289，AUC=0.806。

RNA结合蛋白5Z9WA有388个残基，其中11个是结合残基(图7C和D)。对于这个蛋白质，GraphBind预测了10个真正的结合残基，只有一个真正的结合残基丢失，产生的性能为Rec=0.909，Pre=0.154，F1=0.263，mcc=0.339，AUC=0.938。然而，NucleicNet预测5Z9WA中没有结合残基，所有11个真正的结合残基都被错误地预测为非结合残基，得到Rec=0.000，Pre=0.000，F1=0.000，mcc=-0.041，AUC=0.760。

Feature importance analysis

如上所述，我们从蛋白质结构中提取残基(AF)和二级结构轮廓(SS)的原子特征，以及从蛋白质序列中提取PSSM和HMM轮廓。在本节中，我们将调查不同功能组合对GraphBind的影响。在DNA-129测试中，我们使用以下5种特征组合来评估GraphBind：(I)PSSM，(Ii)HMM，(Iii)PSSM+HMM，(Iv)PSSM+HMM+SS和(V)PSSM+HMM+SS+AF。图8显示了针对不同功能组合的MCC和AUC，补充表S3中报告了详细的指标。

如图8所示，当查看单个特性时，HMM对PSSM有更大的歧视。当结合HMM和PSSM时，GraphBind在MCC上产生了改进，对于不平衡数据，这是一个比AUC更客观的度量。结合二级结构特征进一步提高了GraphBind的性能。最后，结合了所有这些功能的GraphBind产生了最高的MCC，说明这四种特征是互补的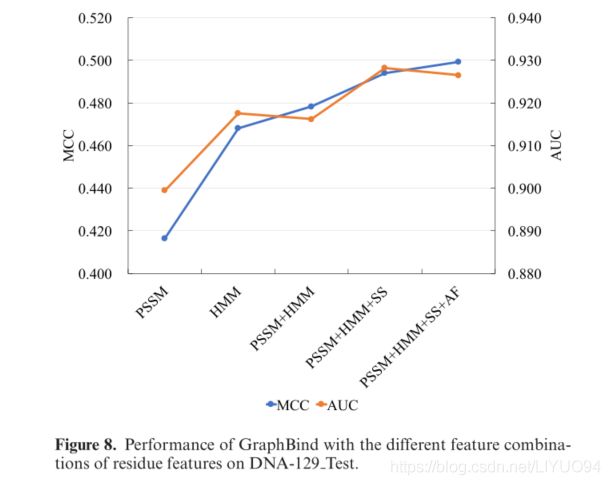

The impact of data augmentation with transferring binding annotations

在本研究中，我们从相似的蛋白质中转移结合注释作为一种数据扩充方法，以增加训练集中的结合残基的数量。转移注释后，训练集中DNA和RNA结合残基的数量分别增加了30.7%和24.3%。我们比较了在有数据扩充和没有数据扩充的训练集上训练的GraphBind的性能。独立测试集上的结果如图9所示(有关更多详细信息，请参见补充表S4)。对于DNA和RNA结合测试集，随着数据的增加，GraphBind的召回率越高，表明识别出的真实结合残基越多。由于DNA/RNA结合残基预测存在数据不平衡的问题，且训练样本多为非结合残基，因此具有重要意义。结果证实了数据增强的好处。

The impact of predicted protein structures on GraphBind

GraphBind是为根据实验蛋白质结构构建图表和进行预测而设计的。为了测试GraphBind是否可以应用于更多没有实验结构的蛋白质群体，我们评估了具有Modeler(50)从蛋白质序列预测的蛋白质结构的GraphBind的性能。我们使用TM-ALIGN(31)来计算PDB(49)中预测结构和实验结构之间的相似度。如补充表S5所示，预测的结构对GraphBind的预测性能有负面影响。主要有两个原因。(I)从结构上下文构建的图直接从蛋白质结构中残基的位置导出，那些与实验结构偏离很大的残基不再包括在结构上下文中，导致构建的图产生负面影响。(Ii)HGNN中的邻接矩阵、节点的位置嵌入和原始边缘特征向量也是基于残差的位置关系。

我们进一步比较了GraphBind和基于序列的方法在由TM分数>0.5的预测蛋白质结构组成的子集上的差异(表4)。TM得分>0.5表示实验结构与预测结构之间有一定的相似性(51)。如表4所示，GraphBind的召回率高于这些基于序列的方法，这表明当蛋白质结构发生变化时，GraphBind更倾向于预测更多的残基作为结合残基，以提高真正结合残基的覆盖率。

综上所述，虽然预测结构会降低GraphBind的性能，但在结构变换不太大的情况下，GraphBind仍具有一定的鲁棒性。这一现象启发我们可以根据蛋白质序列构建图，从而在没有实验结构的情况下将GraphBind应用到更多的蛋白质上。

DISCUSSION

在这一部分中，将潜在的图特征向量可视化，以显示GraphBind的表示能力。此外，在其他配体结合数据集上对GraphBind进行了训练和评估，以评估其泛化能力和实用性。最后，我们讨论了GraphBind的优点和局限性。

GraphBind learns effective latent graph feature vectors for residues

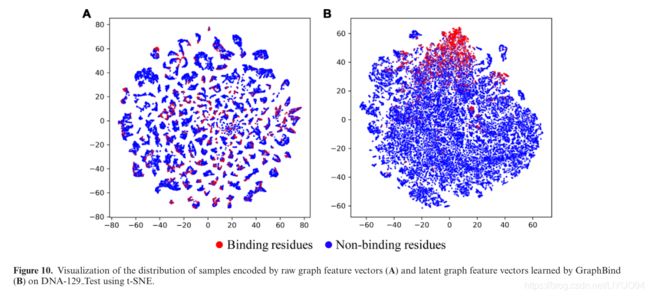
在这一部分中，我们使用t-SNE(52)来可视化由GraphBind学习的原始图特征向量和潜在图特征向量。对于目标残差，一个图的所有节点的原始特征向量之和作为原始图特征向量，其大小为72。GraphBind学习的潜在图特征向量大小为512，是由4个GNN块中嵌入的4个图特征向量拼接而成的。利用T-SNE将高维特征向量投影到2D空间。图10A和图B分别说明了DNA-129测试中由原始图特征向量和潜在图特征向量编码的样本的分布。如图10A所示，我们可以看到结合残基和非结合残基重叠，无法区分。图10B显示大多数结合残基聚集在一起，并与大多数非结合残基分开。结果表明，GraphBind学习的潜在图表示极大地提高了结合残基和非结合残基的可区分性。

Extending GraphBind to other types of ligands

我们探索了GraphBind在识别其他类型的配体结合残基方面的应用。在从ATPbind(54)和Delia(19)收集的包括三种金属离子(即Ca_(2+)、Mn(2+)和Mg_{(2+))的五个基准配体上，我们将GraphBind与TARGET(7)、S-Site(11)、Coach(11)、IonCom(53)、ATPbind(54)和Delia(19)进行了比较和两个生物相关分子(即ATP和血红素)。补充部分S1和补充表S6中描述了五个基准集合的详细信息。由于这些配体的结合残基数量对于我们的深层模型来说足够大，所以选择它们进行泛化测试。我们对这五种类型的配体遵循相同的培训和评估方案，如前几节所述。超级参数在每个配体特定的验证集上进行调整。补充表S7中报告了GraphBind与六种最先进方法的性能比较。图11显示了GraphBind和最先进的Delia的MCC和AUC。结果表明，与第二好的Delia相比，GraphBind在Ca}(2+)、Mn~(2+)、M_(G2+)和血红素方面的MCC和AUC分别提高了0.023-0.107和0.011-0.068。结果表明，基于蛋白质结构背景构建的图比二维距离矩阵更能表达结构信息，并且GraphBind在预测配体结合残基方面也是有效的。

Ligand-general GraphBind-G transferred from ligand- specific GraphBind still achieves a promising performance

GraphBind是一种配体特异性的方法，它训练模型p1er配体来学习配体特异性的结合模式。因此，GraphBind仅限于预测具有少量验证结合残基的配体的结合残基。不同的是，配体通用方法在多个配体的结合残基集合上训练模型，因此它们学习了一大类配体的共同模式，并能够预测看不见的配体的结合残基，但不能预测残基将与哪种配体结合。

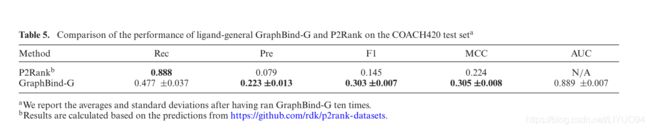
在这里，我们训练了一个配体通用模型GraphBind-G，该模型具有与GraphBind相同的体系结构，并将GraphBind-G与另一种配体通用方法P2Rank(55)进行了比较。为了进行公平的比较，我们在P2Rank的配体通用基准集上对配体通用GraphBind-G进行了训练和评估。该基准集由训练集CHEN11、加入的验证集和测试集COACH420组成。训练集CHEN11包含476个配体和251个蛋白质之间的结合位点，测试集COACH420包含420个蛋白质与各种药物靶标和配体之间的结合位点。GraphBind是一种以残基为中心的方法。然而，在这个基准集中没有给出配体结合残基的注释。根据P2Rank，我们定义了一个配体结合残基，从配体的质量中心到最近的残基原子的距离小于5.5˚A。对于以口袋为中心的P2Rank，我们将预测结合口袋中的所有残基视为预测结合残基。

表5总结了GraphBind-G和P2Rank在COACH420测试集上的性能比较。P2Rank的召回率较高，准确率较低，表明预测的结合残基越多，假阳性率越高。应该注意的是，P2Rank专注于如何准确预测结合位点的口袋位置，并假设结合位点可能含有更大的配体，这可能会导致较高的假阳性率(55)。GraphBind-G的F1得分和MCC分别比P2Rank高0.158和0.081。实验结果表明，基于GNN的GraphBind-G比基于随机森林的P2Rank具有更好的性能，说明了GNN相对于传统机器学习方法的优势，以及本文方法在配体通用结合残基预测上的有效性。GraphBind-G的通用型号也可以在同一网站上作为在线服务提供。

The advantages of GraphBind

GraphBind比几何不可知biLSTMClf具有更好的性能，说明了几何知识的重要性。大多数比较的方法首先提取几何和生物物理化学特征，然后将这些特征送入有监督的分类器以预测结合残基(12，13)。这些方法分离了特征工程和分类。例如，基于深度学习的NucleicNet将结构表示为具有物理化学环境的2D图像，并进一步使用CNNs对结合残基进行分类(13)。然而，GraphBind是以端到端的方式训练的，它能够通过考虑局部结构上下文拓扑来细化几何和生物物理化学特征。总之，GraphBind的优越性能得益于两个方面：(I)基于结构上下文的图表示适合于表示目标残基局部环境的几何和生物物理化学知识；(Ii)HGNN是一种有效的学习高层模式的算法，用于结合残基预测。

The limitations of GraphBind

当前的GraphBind对蛋白质结构进行预测。如表4所示，将预测结构作为GraphBind的输入会降低GraphBind的性能，这表明结构质量与几何知识有关，而几何知识对HGNN非常重要。在未来的工作中，我们希望找到一种新的方法，通过整合蛋白质一级序列来构建异质图，这种方法可能只对结构信息具有鲁棒性。当前GraphBind的另一个潜在扩展是增加预测特定DNA/RNA相互作用组分的模块，这将为深入理解相互作用机制提供更多有用的线索(13)。

CONCLUSION

在这项研究中，我们提出了GraphBind，蛋白质结构上下文嵌入规则，通过分层图神经网络(HGNN)学习来识别核酸结合残基。考虑到核酸结合残基主要由蛋白质三级结构的局部模式和生物物理化学环境决定，我们首次提出了一种基于结构上下文的图表示法来表示残基及其数目变化的无序邻域的生物物理化学特征和几何知识，并且具有旋转和平移不变性。在此基础上，提出了利用HGNN从图的边特征向量和节点特征向量中学习有效的固定大小的隐含表示。结果表明，GraphBind在识别核酸结合残基方面具有优越性，在识别多种配体和一般配体的结合残基方面具有推广能力。

DATA AVAILABILITY

数据和网络服务器可在http://www免费获得。Cn/Bioinf/GraphBind/，GraphBind的源代码可以在http://www.csBio.sjtu.edu.cn/Bioinf/GraphBind/Sourecode.html上找到。

SUPPLEMENTARY DATA

补充数据可在NAR Online上获得。

FUNDING

国家重点研究发展计划[2018YFC0910500]；国家自然科学基金[62073219,61725302,61671288,61903248]；上海市科学技术委员会[17JC1403500，20S11902100]。开放存取费用资助：国家自然科学基金[61725302]。利益冲突声明。无人宣布。