[python] Sklearn（一）之最小二乘法

最小二乘法是一个很实用的工具，它的概念很容易理解，但用程序实现几个矩阵乘法有可能很容易搞错了，但是会python就啥都会了，难道不是么。废话不多说，上代码

一、基础版的最小二乘法demo

from sklearn import linear_model
reg = linear_model.LinearRegression()

#reg.fit([(0,0),(1,1),(2,2)],[0,1,2])#拟合，写法1
X=[(0,0),(1,1),(2,2)]
Y=[0,1,2]
reg.fit(X,Y)#拟合，写法2
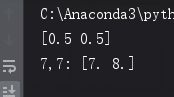
print(reg.coef_)#输出拟合出来的参数
print("7,7:",reg.predict([[7, 7],[8,8]]))#输入[7,7]和[8,8]两组数据进行简单预测

看了代码就会了吧，就是这么容易，简要说明一下：
输入数据X为[[0,0],[1,1],[2,2]]
标签数据Y为[0,1,2]
然后用这三组数据进行拟合的到模型，使用[7,7]和[8,8]两组测试数据进行预测，结果如下

二、进阶版的最小二乘法demo

如果标签不是个标量，也是两个值呢，可不可以使用最小二乘法预测？答案是肯定可以的，是三个值也是可以预测的，只需要把Y值进行相应修改即可
简单版本

from sklearn import linear_model
reg = linear_model.LinearRegression()
#reg.fit([(0,0),(1,1),(2,2)],[(0,0),(1,1),(2,2)])#写法1
X=[(0,0),(1,1),(2,2)]
Y=[(0,0),(1,1),(2,2)]
reg.fit(X,Y)#拟合，写法2
print(reg.coef_)#输出拟合出来的参数
print("7,7:",reg.predict([[7, 7],[8,8]]))#输入[7,7]和[8,8]两组数据进行简单预测

结果：

三、实际应用：

最小二乘法用python就是如此简单。如果上面两个段落搞懂了就行了，可以跳过本节，本节只是记载了一个实际应用，也想留给自己以后看的。
我搞了两个测试数据，从这里免费下载。这两组数据是进行匹配得到的结果，它们靠同名点ID进行形成对应关系，gcp文件里面是经度、纬度；pxy文件里面是对应的像素X、像素Y，我想拟合出模型，输入一个点，通过模型可以预测到另一个点，我的想法是把经纬度转换为像素值，然后像素值仿射像素值效果应该好点，上代码：

from sklearn import linear_model#最小二乘法
import math


def readPxy(PxyPath):#读pxy文件中所有点
    result = dict()
    with open(PxyPath, "r+") as fp:
        txt = fp.readlines()
        print(txt)
        for i in range(1,len(txt)):
            # print(txt[i])
            list_temp = txt[i].split()
            id = list_temp[0]
            x = float(list_temp[1])
            y = float(list_temp[2])
            result[id]=(x,y)

    return result

def TransforGeo2Pix(GcpDicInfo,Lng_OFF,Lat_OFF,Resolution):
    result = dict()
    for key, value in GcpDicInfo.items():
        result[key]=((value[1]-Lng_OFF)/Resolution,(Lat_OFF - value[0])/Resolution)
    return result


if __name__ == '__main__':
    gcpPath = "E:/temp/1.gcp";
    pxyPath = "E:/temp/1.pxy";
    Lng_OFF = 113.999990991;
    Lat_OFF = 31.333342342333;
    Resolution = 1.8018e-05;
    GcpDicInfo=readPxy(gcpPath)
    PxyDicInfo=readPxy(pxyPath)
    # print("gcp:",GcpDicInfo)
    # print("pxy:",PxyDicInfo)
    Gcp2PxyDicInfo = TransforGeo2Pix(GcpDicInfo,Lng_OFF,Lat_OFF,Resolution)#用Gcp的点转换成像素
    print("gcpPxy:",Gcp2PxyDicInfo)
    reg = linear_model.LinearRegression()#最小二乘法

    X=[]
    Y=[]
    for key_Gcp, value_Gcp in Gcp2PxyDicInfo.items():#利用标签把对应的数值捋顺
        X.append(value_Gcp)
        for key_Pxy, value_Pxy in PxyDicInfo.items():
            if(key_Gcp==key_Pxy):
                Y.append(value_Pxy)
                break
    print("X:",X)
    print("Y:",Y)
    reg.fit(X,Y)#训练
    print(reg.coef_)#输出拟合的权重

    #使用训练的数据进行检验一下效果怎么样
    for key_Gcp, value_Gcp in Gcp2PxyDicInfo.items():
        PreResult = reg.predict([value_Gcp])
        print("{}:".format(value_Gcp), PreResult)
        print("lable:",PxyDicInfo[key_Gcp])
        XError = abs(PxyDicInfo[key_Gcp][0]-PreResult[0][0])
        YError = abs(PxyDicInfo[key_Gcp][1]-PreResult[0][1])

        AllError = math.sqrt(XError*XError + YError * YError)
        print("XError:{},YError:{},AllError:{}\n".format(XError, YError, AllError))

效果还行，把训练数据带入进去，有些地方与实际相差30多像素：