哈希表
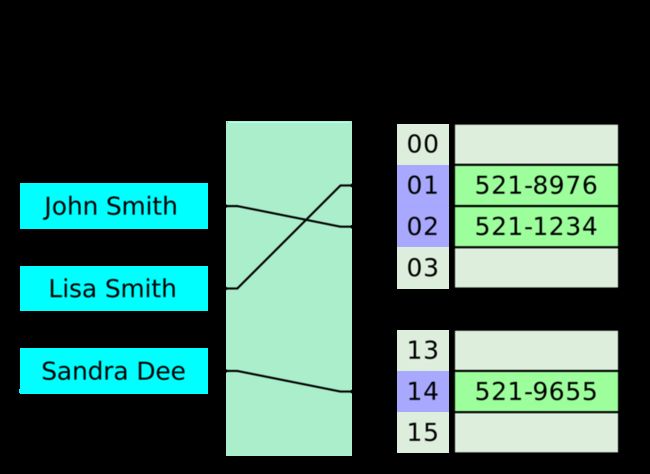
哈希表是一种键值映射的数据结构。哈希表中,数据以数组格式存储,其中每个数据值都有自己唯一的索引值,索引值通过哈希表的哈希函数计算得到。
下面两步将键哈希值转化成哈希表的索引值。
- 哈希值 = 哈希函数(键)
- 索引值 = 哈希值 % 哈希表长度
冲突解决方法
有限长度下的哈希表,冲突不可避免。解决冲突的两种方法,拉链法和开放寻址。
拉链法
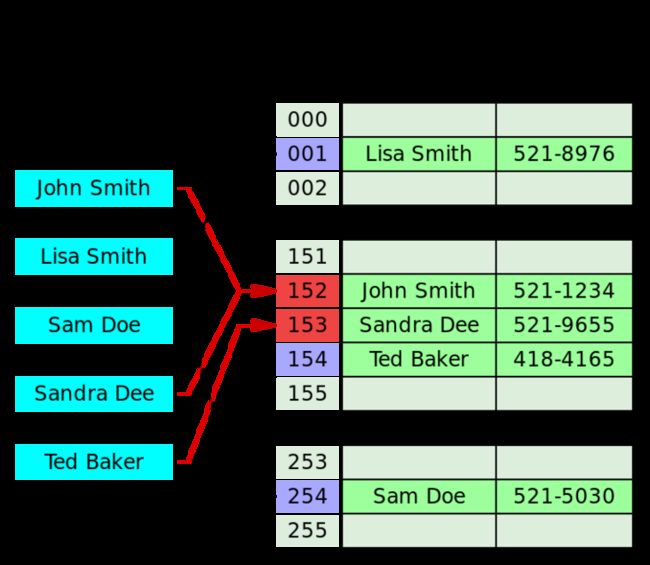
将冲突位置的元素构造成链表。添加数据发生冲突时,将元素追加到链表。如下图,当添加 "Sandra Dee"时,计算出索引值为152与“John Smith” 发生冲突,然后将它追加到链表。
开放寻址
以当前冲突位置为起点,按照一定规则探测空位置把元素插进去。比较简单的方式是线性探测,它会按照固定的间隔(通常是1)循环进行查找。
如下图,“Sandra Dee”添加时与 “John Smith” 相冲突,通过探测空位置插入到153,然后添加“Ted Baker”发现与“Sandra Dee”相冲突,往后探测154空位置插入。
性能
负载因子
负载因子的值是条目数占用哈希桶比例,当负载因子超过理想值时,哈希表会进行扩容。比如哈希表理想值 0.75,初始容量 16,当条目超过 12 后哈希表会进行扩容重新哈希。0.6 和 0.75 是通常合理的负载因子。
$$ {\displaystyle loadfactor\ (\alpha )={\frac {n}{k}}} $$
- $n$ 哈希表中的条目数。
- $k$ 桶的数量。
影响哈希表性能的两个主要因素
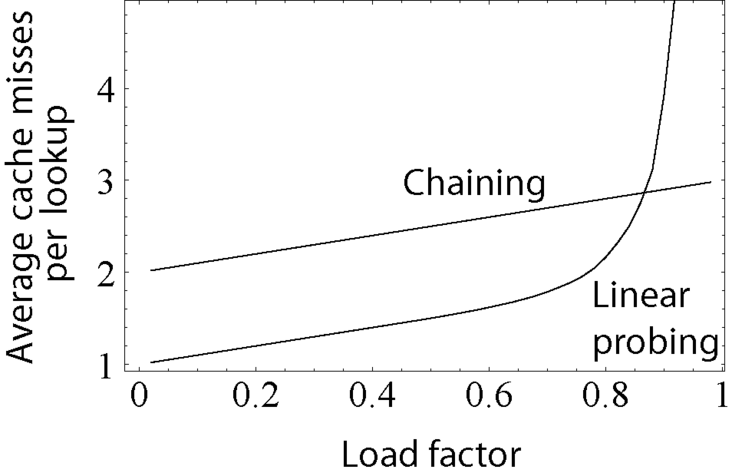
- 缓存丢失。随着负载因子的增加缓存丢失数量上升,而搜索和插入性能会因此大幅下降。
- 扩容重新哈希。调整大小是一项极其耗时的任务。设置合适的负载因子可以控制扩容次数。
下图展示了随着负载因子增加,缓存丢失的数量开始上升,0.8后开始迅速攀升。
HashMap
关于 HashMap 解读一下它的 hash 方法和冲突树化两个地方。
关于hash()
取key的hashCode值,然后将高16位与低16位进行异或、最后取模运算。
static final int hash(Object key) { //jdk1.8 & jdk1.7
int h;
// h = key.hashCode() 取hashCode值
// h ^ (h >>> 16) 将高16位与低16位进行异或
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
// jdk1.7
static int indexFor(int h, int length) {
return h & (length-1);
}
// jdk1.8
(n - 1) & hash高16位与低16位进行异或是为了加大低位的随机性。
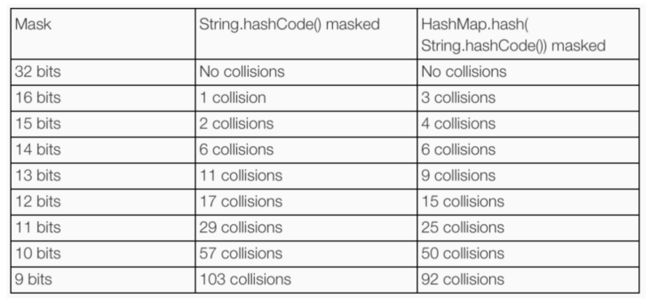
关于随机性,网上有个测试例子:他随机选取了352个字符串,测试不同长度数组下的碰撞概率。
结果显示,当HashMap数组长度为 2^9 = 512 的时候,直接取hashCode冲突103次,进行高低异或后冲突92次。
https://www.todaysoftmag.com/...
冲突树化
HashMap解决冲突使用拉链法。jdk1.8 中,当一个桶链表节点超过TREEIFY_THRESHOLD=8后,链表会转换为红黑树,当桶中节点移除或重新哈希少于 UNTREEIFY_THRESHOLD=6时,红黑树会转变为普通的链表。
链表取元素是从头结点一直遍历到对应的结点,时间复杂度是O(N) ,红黑树基于二叉树结构,时间复杂度为O(logN) ,所以当元素个数过多时,用红黑树存储可以提高搜索的效率。但是单个树节点需要占用的空间大约是普通节点的两倍,所以使用树和链表是时空权衡的结果。
树化阀值为什么是 8 ?
HashMap 文档有这么一段描述。大体意思是,哈希桶上的链表节点数量呈现泊松分布。
Ideally, under random hashCodes, the frequency of * nodes in bins follows a Poisson distribution * (http://en.wikipedia.org/wiki/Poisson_distribution) with a * parameter of about 0.5 on average for the default resizing * threshold of 0.75, although with a large variance because of * resizing granularity. Ignoring variance, the expected * occurrences of list size k are (exp(-0.5) * pow(0.5, k) / * factorial(k)). The first values are: * * 0: 0.60653066 * 1: 0.30326533 * 2: 0.07581633 * 3: 0.01263606 * 4: 0.00157952 * 5: 0.00015795 * 6: 0.00001316 * 7: 0.00000094 * 8: 0.00000006 * more: less than 1 in ten million
什么是泊松分布?
泊松分布就是描述某段时间内,事件具体的发生概率。柏松分布可以通过平均数估算出某个事件的出现概率。
$$ P(N(t) = n) = \frac{(\lambda t)^n e^{-\lambda t}}{n!} $$
- $P$ 概率;
- $N$ 某种函数关系;
- $t$ 时间;
- $n$ 出现的数量;
比如,一个程序员每天平均写3个Bug,表示为\( P(N(1) = 3) \)。由此还可以得到下面:
他明天写1个Bug的概率:0.1493612051
他明天写2个Bug的概率:0.2240418077
他明天写3个Bug的概率:0.2240418077
他明天写10个Bug的概率:0.0008101512
/**
* @param n 节点数量
* @param r 平均数量
*/
public static String poisson(int n, double r) {
double value = Math.exp(-r) * Math.pow(r, n) / IntMath.factorial(n);
return new BigDecimal(value).setScale(10, ROUND_HALF_UP).toPlainString();
}假设HashMap有 \( n \) 条数据,负载因子为 \( k \) ,那么HashMap长度最小值为 \( \frac{n}{k} \) ,最大约为 \( \frac{2n}{k} \) (容量必须是 2 的幂) 所以平均值是 \( \frac{3n}{2k} \),每个桶的平均节点数量为
$$ n \div(\frac{3n}{2k})= \frac{2k}{3} = \frac{2\times 0.75}{3} = 0.5 $$
HashMap 默认负载因子为 0.75,所以每个桶的平均节点数量 0.5,代入柏松公式得到下面数据
1个桶中出现1个节点的概率:0.3032653299 1个桶中出现2个节点的概率:0.0758163325 1个桶中出现3个节点的概率:0.0126360554 1个桶中出现4个节点的概率:0.0015795069 1个桶中出现5个节点的概率:0.0001579507 1个桶中出现6个节点的概率:0.0000131626 1个桶中出现7个节点的概率:0.0000009402 1个桶中出现8个节点的概率:0.0000000588
树化是哈希极度糟糕下不得已而为之的做法,而一个桶出现 8 个节点的概率不到千万分之一,所以将TREEIFY_THRESHOLD=8 。
小结
哈希表是一种键值映射的数据结构。解决冲突有两种方法拉链法和开放寻址。合理设置负载因子和初始容量避免过多的扩容操作和缓存丢失。 理解HashMap的 hash 方法和冲突树化。