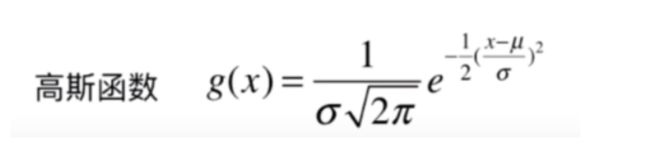机器学习（四）SVM深入理解

机器学习（四）SVM深入理解

〇、SVM原理与线性不可分

有关于SVM算法的基本原理可以在我的上一篇文章中找到：机器学习（三）线性判别准则与线性分类编程实践，这里不再多提。

在实际应用中，大多情况下数据并不是线性可分的，这个时候满足这样条件的超平面根本就不存在，而本文将主要针对了解SVM算法在解决线性不可分类时，对特征集进行多项式、核函数转换（升维）将其转换为线性可分类问题的思想。

所以就有了核函数。

核函数

核函数特点：

• 不需要每次都具体计算出原始样本点映射的新的无穷维度的样本点，直接使用映射后的新的样本点的点乘计算公式即可；

• 减少计算量

• 减少存储空间

• 一般将原始样本变形，通常是将低维的样本数据变为高维数据，存储高维数据花费较多的存储空间；使用核函数，不用考虑原来样本改变后的样子，也不用存储变化后的结果，只需要直接使用变化的结果进行运算并返回运算结果即可；

• 核函数的方法和思路不是 SVM 算法特有，只要可以减少计算量和存储空间，都可以设计核函数方便运算；

• 对于比较传统的常用的机器学习算法，核函数这种技巧更多的在 SVM 算法中使用；

1. 多项式核函数：

代码格式：

from sklearn.svm import SVC

svc = SVC(kernel = 'ploy')

**思路：**设计一个函数（K(x,x))，传入原始样本(x(i)、xi)，返回添加了多项式特征后的新样本的计算结果(x’(i) , xi) ;

**内部过程：**先对x、xj添加多项式，得到: xi)、xi)，再进行运算: x(i) .x(i) ;

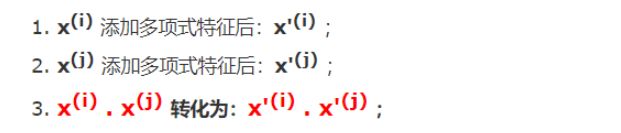
其实不使用核函数也能达到同样的目的，这里核函数相当于一个技巧，更方便运算;

2. 高斯/RBF核函数：

高斯核函数也叫RBF核（Radia Basis Function Kernel），核函数依赖升维使得原本线性不可分的数据变得线性可分。高斯核本质是在衡量样本和样本之间的“相似度”，在一个刻画“相似度”的空间中，让同类样本更好的聚在一起，进而线性可分。

思路：

业务的目的是样本分类，采用的方法：按一定规律统一改变样本的特征数据得到新的样本，新的样本按新的特征数据能更好的分类，由于新的样本的特征数据与原始样本的特征数据呈一定规律的对应关系，因此根据新的样本的分布及分类情况，得出原始样本的分类情况。

应该是试验反馈，将样本的特征数据按一定规律统一改变后，同类样本更好的凝聚在了一起；

高斯核和多项式核干的事情截然不同的，如果对于样本数量少，特征多的数据集，高斯核相当于对样本降维；

高斯核的任务：找到更有利分类任务的新的空间。

一、代码实现

1. 引包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

2. 定义函数

#非线性SVM分类,当degree为0表示线性
def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])

#绘制决策边界
def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape) 
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, cmap=custom_cmap)

#核函数
def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
    ])

#高斯核函数
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

二、例子重做

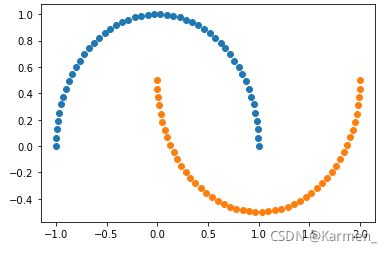
1. 月亮数据集

#使用生成的数据
x_moom, y_moom = datasets.make_moons() 
#展示数据
plt.scatter(x_moom[y_moom==0,0],x_moom[y_moom==0,1]) 
plt.scatter(x_moom[y_moom==1,0],x_moom[y_moom==1,1])
plt.show()

#随机生成噪声点，random_state是随机种子，noise是方差
x_moom, y_moom = datasets.make_moons(noise=0.15,random_state=520) 

#展示处理过后的数据
plt.scatter(x_moom[y_moom==0,0],x_moom[y_moom==0,1]) 
plt.scatter(x_moom[y_moom==1,0],x_moom[y_moom==1,1])
plt.show()

• 多项式拟合

  #多项式
  poly_svc_moom = PolynomialSVC(degree=5,C=10)
  #拟合
  poly_svc_moom.fit(x_moom,y_moom)
  #打印权重和截距
  print("权重w:",poly_svc_moom.named_steps['linearSVC'].coef_[0])
  print("截距b:",poly_svc_moom.named_steps['linearSVC'].intercept_[0])
  # 绘制决策边界
  plot_decision_boundary(poly_svc_moom,axis=[-1.5,2.5,-1.5,2.5])
  # 绘制原始数据
  plt.scatter(x_moom[y_moom==0,0],x_moom[y_moom==0,1]) 
  plt.scatter(x_moom[y_moom==1,0],x_moom[y_moom==1,1])
  plt.show()
  

  

• 高斯拟合

  #高斯核处理 参数为1
  rbf_svc_moom = RBFKernelSVC(1)
  #拟合
  rbf_svc_moom.fit(x_moom,y_moom)
  
  #打印对偶系数以及截距
  print("系数w:",rbf_svc_moom.named_steps['svc'].dual_coef_)
  print("截距b:",rbf_svc_moom.named_steps['svc'].intercept_)
  # 绘制决策边界
  plot_decision_boundary(rbf_svc_moom,axis=[-1.5,2.5,-1.0,1.5])
  # 绘制原始数据
  plt.scatter(x_moom[y_moom==0,0],x_moom[y_moom==0,1]) 
  plt.scatter(x_moom[y_moom==1,0],x_moom[y_moom==1,1])
  plt.show()
  

  

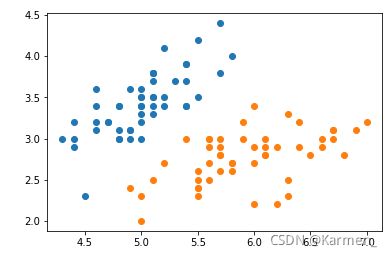
2. 鸢尾花数据集

iris = datasets.load_iris()

x_iris = iris.data
y_iris = iris.target

x_iris = x_iris [y_iris<2,:2] #只取y<2的类别，也就是0 1 并且只取前两个特征
y_iris = y_iris[y_iris<2] # 只取y<2的类别

# 分别画出类别0和1的点
plt.scatter(x_iris[y_iris==0,0],x_iris[y_iris==0,1]) 
plt.scatter(x_iris[y_iris==1,0],x_iris[y_iris==1,1])
plt.show()

• 多项式拟合

  #多项式
  poly_svc_iris = PolynomialSVC(degree=5,C=10)
  #拟合
  poly_svc_iris.fit(x_iris,y_iris)
  #打印权重和截距
  print("权重w:",poly_svc_iris.named_steps['linearSVC'].coef_[0])
  print("截距b:",poly_svc_iris.named_steps['linearSVC'].intercept_[0])
  # 绘制决策边界
  plot_decision_boundary(poly_svc_iris,axis=[4,7.5,1,4.5]) # x,y轴都在-3到3之间
  # 绘制原始数据
  plt.scatter(x_iris[y_iris==0,0],x_iris[y_iris==0,1]) 
  plt.scatter(x_iris[y_iris==1,0],x_iris[y_iris==1,1])
  plt.show()
  

  

• 高斯拟合

  #高斯核处理 参数为1
  rbf_svc_iris = RBFKernelSVC(1)
  #拟合
  rbf_svc_iris.fit(x_iris,y_iris)
  #打印对偶系数以及截距
  print("系数w:",rbf_svc_iris.named_steps['svc'].dual_coef_)
  print("截距b:",rbf_svc_iris.named_steps['svc'].intercept_)
  # 绘制决策边界
  plot_decision_boundary(rbf_svc_iris,axis=[4,7.5,1,4.5])
  # 绘制原始数据
  plt.scatter(x_iris[y_iris==0,0],x_iris[y_iris==0,1]) 
  plt.scatter(x_iris[y_iris==1,0],x_iris[y_iris==1,1])
  plt.show()
  

  

四、总结

本文对上一次学到的SVM算法作了拓展和补充，解决了在实际应用中如何应对非线性不可分的疑惑。

五、参考文章

醉意丶千层梦： 基于Sklearn+matlab绘制SVM决策函数

平行叶子： AVM补充