?p=24231

Boosting 是一类集成机器学习算法，涉及结合许多弱学习器的预测。

弱学习器是一个非常简单的模型，尽管在数据集上有一些技巧。在开发实用算法之前很久，Boosting 就是一个理论概念，而 AdaBoost（自适应提升）算法是该想法的第一个成功方法。

AdaBoost算法包括使用非常短的（一级）决策树作为弱学习者，依次添加到集合中。每一个后续的模型都试图纠正它之前的模型在序列中做出的预测。这是通过对训练数据集进行权衡来实现的，将更多的注意力放在先前模型出现预测错误的训练实例上。

在本教程中，您将了解如何开发用于分类和回归的 AdaBoost 集成。

完成本教程后，您将了解：

AdaBoost集成是一个由决策树依次添加到模型中而形成的合集。
如何使用 AdaBoost 集成通过 scikit-learn 进行分类和回归。
如何探索 AdaBoost 模型超参数对模型性能的影响。
添加了网格搜索模型超参数的示例。

教程概述

本教程分为四个部分；他们是：

AdaBoost 集成算法
AdaBoost API
用于分类的 AdaBoost
用于回归的 AdaBoost
AdaBoost 超参数
探索树的数量
探索弱学习
探索学习率
探索替代算法
网格搜索 AdaBoost 超参数

AdaBoost 集成算法

Boosting "Boosting") 是指一类机器学习集成算法，其中模型按顺序添加，序列中较晚的模型纠正序列中较早模型所做的预测。

AdaBoost是“ Adaptive Boosting ”的缩写，是一种提升集成机器学习算法，并且是最早成功的提升方法之一。

我们称该算法为 AdaBoost 是因为与以前的算法不同，它可以自适应地调整弱假设的错误

— A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting, 1996.

AdaBoost 结合了来自短的一级决策树的预测，称为决策树桩，尽管也可以使用其他算法。决策树桩算法被用作 AdaBoost 算法，使用许多弱模型并通过添加额外的弱模型来纠正它们的预测。

训练算法涉及从一个决策树开始，在训练数据集中找到那些被错误分类的例子，并为这些例子增加更多的权重。另一棵树在相同的数据上训练，尽管现在由误分类错误加权。重复此过程，直到添加了所需数量的树。

如果训练数据点被错误分类，则该训练数据点的权重会增加（提升）。使用新的权重构建第二个分类器，这些权重不再相等。同样，错误分类的训练数据的权重增加，并重复该过程。

— Multi-class AdaBoost, 2009.

该算法是为分类而开发的，涉及组合集成中所有决策树所做的预测。还为回归问题开发了一种类似的方法，其中使用决策树的平均值进行预测。每个模型对集成预测的贡献根据模型在训练数据集上的性能进行加权。

新算法不需要弱假设准确性的先验知识。相反，它适应这些准确性并生成加权多数假设，其中每个弱假设的权重是其准确性的函数。

— A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting, 1996.

现在我们熟悉了 AdaBoost 算法，让我们看看如何在 Python 中拟合 AdaBoost 模型。

AdaBoost Scikit-Learn API

scikit-learn Python 机器学习库为机器学习提供了 AdaBoost 集成的实现。

首先，通过运行以下脚本确认您使用的版本：

# 检查scikit-learn版本

import sklearn

print(sklearn.\_\_version\_\_)

运行该脚本将输出的 scikit-learn 版本。

在构建模型的过程中使用了随机性。这意味着每次在相同的数据上运行该算法时，都会产生一个略有不同的模型。

当使用具有随机学习算法的机器学习算法时，通过在多次运行或重复交叉验证中平均其性能来评估它们是很好的做法。在拟合最终模型时，最好是增加树的数量，直到模型的方差在重复评估中减少，或者拟合多个最终模型并平均其预测值。

让我们来看看如何为分类和回归开发 AdaBoost 集成。

用于分类的 AdaBoost

在本节中，我们将研究使用 AdaBoost 解决分类问题。

首先，我们可以创建一个包含 1,000 个示例和 20 个输入特征的合成二元分类问题。

下面列出了关键代码片段示例。

# 测试分类数据集

from skar.dtasts imprt me_clssificaton


# 对数据集进行总结

pin(X.shp y.hae)

运行示例创建数据集并总结输入和输出的维度。

接下来，我们可以在这个数据集上评估 AdaBoost 算法。

我们将使用重复的分层k-折交叉验证来评估该模型，有三个重复和10个折。我们将报告该模型在所有重复和折中的准确性的平均值和标准偏差。

# 评估adaboost算法的分类

from numpy import mean


# 定义模型

mdl = ABster()

# 评估该模型

cv = Reeio(n\_is=10, n\_pe=3, rn_tt=1)
s=-1, rr_se='raise')

# 报告性能

prt('ccrac %.3f (%.f)' % (ean(scoes),std(n_ces)))

运行示例报告模型的均值和标准偏差准确度。

注意：您的结果考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

在这种情况下，我们可以看到具有默认超参数的 AdaBoost 集成在此测试数据集上实现了约 80% 的分类准确率。

我们也可以使用AdaBoost模型作为最终模型，并进行预测分类。

首先，AdaBoost集合在所有可用的数据上进行拟合，然后可以调用predict()函数对新数据进行预测。

下面的例子在我们的二元分类数据集上演示了这一点。

# 使用adaboost进行分类预测

from sldat  s imprt mke_lassicain

#定义模型

moel = AdBoser()

# 在整个数据集上拟合模型

mdl.t(X, y)

# 进行一次预测



yhat = mdepreict(ow)

prnt('Preicte Clas: %d'  yht\[0\])

运行示例在整个数据集上拟合 AdaBoost 集成模型，然后用于对新数据行进行预测，就像我们在应用程序中使用模型时一样。

现在我们熟悉了使用 AdaBoost 进行分类，让我们看一下用于回归的 API。

用于回归的 AdaBoost

在本节中，我们将研究使用 AdaBoost 解决回归问题。

首先，我们可以创建一个具有 1,000 个示例和 20 个输入特征的综合回归问题。

下面列出了完整的示例。

# 测试回归数据集
fromrn.se impr mkergrsion

# 定义数据集
X, y = mkresion(naps=1000,n_eaes=20, nom=15, nse=0.1,ramtae=6)

# 对数据集进行总结

prntX.she, y.hae)

运行示例创建数据集并总结输入和输出的维度。

接下来，我们可以在这个数据集上评估 AdaBoost 算法。

正如我们在上一节所做的那样，我们将使用重复的 k 折交叉验证来评估模型，重复 3 次和 10 次。我们将报告模型在所有重复和折中的平均绝对误差 (MAE)。使 MAE 为负值，使其最大化而不是最小化。这意味着负 MAE 越大越好，完美模型的 MAE 为 0。

下面列出了完整的示例。

# 评估adaboost集合的回归效果

from numpy import mean




# 定义模型

mel = Aar()

# 评估该模型

KFld(n\_lit=10, n\_pes=3, rndstt=1)

crss(mde, X, y, sorng='n\_mea\_aoluteeror', cv=cv, nobs=-1, ercr='raise')

# 报告性能

rit('MAE: %.3f (%.3f)' % (mean(sc), std(_cres)))

运行示例报告模型的均值和标准偏差准确度。

注意：您考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

在这种情况下，我们可以看到具有默认超参数的 AdaBoost 集成实现了大约 100 的 MAE。

我们还可以使用 AdaBoost 模型作为最终模型并对回归进行预测。

首先，AdaBoost 集成拟合所有可用数据，然后可以调用_predict()_函数对新数据进行预测。

下面的示例在我们的回归数据集上演示了这一点。

# 用于预测回归的adaboost集成

import maeon





# 定义模型

moel = Botsor()

# 在整个数据集上拟合该模型

fit(X, y)

# 做一个单一的预测


 peict(row)

pit('Peon: %d' % ht\[0\])

运行示例在整个数据集上拟合 AdaBoost 集成模型，然后用于对新数据行进行预测，就像我们在应用程序中使用模型时一样。

现在我们已经熟悉了使用 scikit-learn API 来评估和使用 AdaBoost 集成，让我们看一下配置模型。

AdaBoost 超参数

在本节中，我们将仔细研究一些您应该考虑调整 AdaBoost 集成的超参数及其对模型性能的影响。

探索树的数量

AdaBoost 算法的一个重要超参数是集成中使用的决策树的数量。

回想一下，集成中使用的每个决策树都被设计为弱学习器。也就是说，它比随机预测有技巧，但技巧不高。因此，使用一级决策树，称为决策树桩。

添加到模型中的树的数量必须很高，模型才能正常工作，通常是数百甚至数千。

树的数量可以通过“ _n_ ”参数设置，默认为 50。

下面的示例探讨了值在 10 到 5,000 之间的树数量的影响。

# 探索adaboost集成的树数对性能的影响

from numpy import mean




# 获取数据集

def gdet():

X, y = ae\_scon(n\_spes=1000, nftus=20, inve=15, n\_rant=5, ram\_ae=6)

retrn X, y



# 获得要评估的模型列表

def gemls():

mels = dct()

# 定义要考虑的树的数量


for n in n_res:
mols\[str(n)\] = AaBstsfern_titos=n)

etrn moel



# 用交叉验证法评估一个给定的模型

def evat_oe(odl, X, y):

# 定义评估程序

cv = RpdStfKFol(n_pis=10, nrpt=3, andoste=1)

# 评估模型并收集结果
scs = cs\_vore(moel, X, y, scng='ccrcy', cv=cv, n\_jobs=-1)
return sces


# 定义数据集

X, y = gedast()

# 获得要评估的模型

odls = emols()

# 评估模型并存储结果

rslt, nmes = lst(), lst()

for nae, moel in odels.ims():

# 评估模型

scor = eateel(mdel, X, y)

# 存储结果

ruls.aped(scrs)

na   e.aped(nae)

# 总结表现

prnt('>%s %.3f (%3f)' % (nme, man(scrs), std(soes)))

# 绘制模型的性能，进行比较


p.shw()

运行示例首先报告每个数量的决策树的平均准确度。

注意：考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

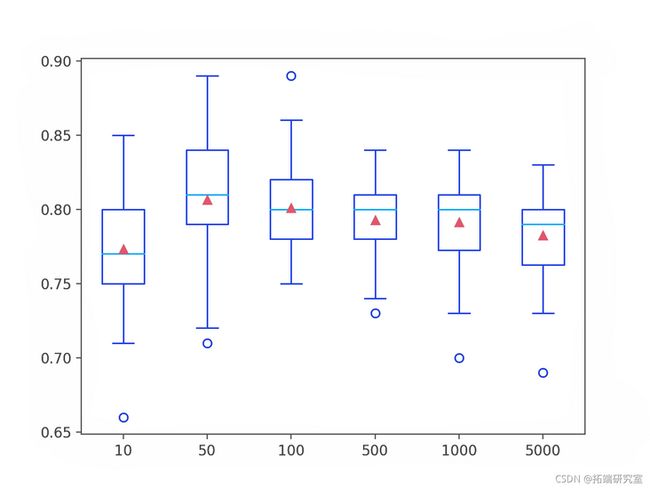
在这种情况下，我们可以看到该数据集的性能在大约 50 棵树之前有所提高，然后下降。这可能是在添加额外的树后集成过度拟合训练数据集的问题。

为每个配置数量的树的准确度分数分布创建了一个箱线图。

我们可以看到模型性能和集成大小的总体趋势。

AdaBoost 集成大小与分类精度的箱线图

探索弱学习者

默认情况下，只有一个层次的决策树被用作弱学习器。

我们可以通过增加决策树的深度，使合集中使用的模型不那么弱（更有技巧）。

下面的例子探讨了增加DecisionTreeClassifier弱学习器的深度对AdBoost组合的影响。

# 探索adaboost集成树深度对性能的影响

from numpy import mean





# 获得数据集

def ettst():


rtrn X, y



# 获得一个要评估的模型列表

def gtodes():
modls = di()

# 探索从1到10的深度

for i in rane(1,11):

# 定义基本模型

bae = DisioTer(mxdph=i)
# 定义集合模型

modls\[tr(i)\] = Bost(bseimaor=bse)

rtun moes



# 用交叉验证法评估一个给定的模型

def elaeel(moel, X, y):

# 定义评估程序

cv = RpaedSifdKod(n_pis=10, nepts=3, rndoste=1)
# 评估模型并收集结果

soes = cro\_acoe(moel, X, y,scorng='ccray', cv=cv, \_obs=-1)

return scos



# 定义数据集

X, y = edatet()

# 获得要评估的模型

mols = etels()

# 评估模型并存储结果

rsults, nes = lst(), lst()

for ame, odel in mdelsts():

# 评估模型

scrs = evlel(moel, X, y)

# 存储结果

rsls.aped(scos)

naes.apend(nme)

# 总结表现

pit('>%s %.3f (%.3f)' % (nae, man(scors), std(scres)))

# 绘制模型的性能，以便进行比较


p.hw()

运行示例首先报告每个配置的弱学习器树深度的平均准确度。

注意：考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

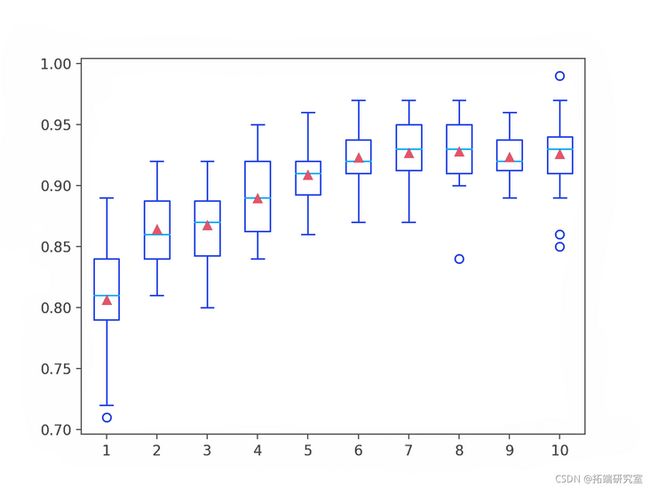
在这种情况下，我们可以看到随着决策树深度的增加，集成在该数据集上的性能也有所提高。

为每个配置的弱学习器深度的准确度分数分布创建了一个盒须图。

我们可以看到模型性能和弱学习器深度的总体趋势。

AdaBoost Ensemble 弱学习器深度与分类精度的箱线图

探索学习率

AdaBoost 还支持控制每个模型对集成预测的贡献的学习率。

这由“ learning_rate ”参数控制，默认情况下设置为 1.0 或全部贡献。根据集成中使用的模型数量，更小或更大的值可能是合适的。模型的贡献与集成中的树数量之间存在平衡。

更多的树可能需要更小的学习率；更少的树可能需要更大的学习率。通常使用 0 到 1 之间的值，有时使用非常小的值以避免过度拟合，例如 0.1、0.01 或 0.001。

下面的示例以 0.1 的增量探索了 0.1 和 2.0 之间的学习率值。

# 探索adaboost集合学习率对性能的影响

from numpy import mean

from numpy import std





# 获取数据集

def ge_taet() 



# 获得要评估的模型列表

def e_moels():

mods = dct()

# 探索从0.1到2的学习率，增量为0.1

for i in ane(0.1, 2.1, 0.1):

key = '%.3f' % i

mdls\[key\] = AdaBoo(leag_te=i)





# 用交叉验证法评估一个给定的模型

def vaatodl(moel, X, y):

# 定义评估程序

cv = RepeSatiKFld(n\_slts=10, n\_epts=3, ado_tae=1)

# 评估模型并收集结果

sces = csslsre(mel, X, y, soing='cacy', cv=cv, njs=-)




# 定义数据集

X, y = ge_dtet()

# 获得要评估的模型

model= et_oels()

# 评估模型并存储结果


for ne, moel in mode.itms():

# 评估模型

scos =valueoel(, X, y)

# 存储结果

reslt.pped(scors)

naeppend(ame)

# 总结表现


# 绘制模型的性能，以便进行比较



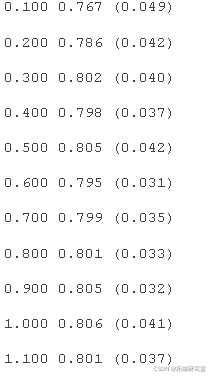
ot.ow()

运行示例首先报告每个配置的学习率的平均准确度。

注意：考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

在这种情况下，我们可以看到 0.5 到 1.0 之间的相似值，之后模型性能下降。

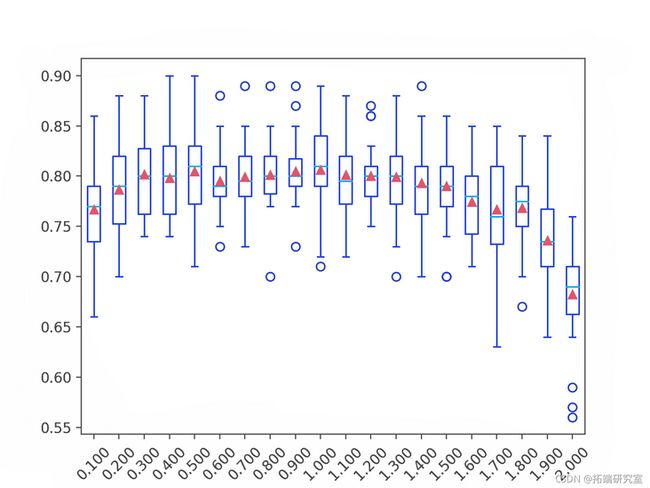
为每个配置的学习率的准确度分数分布创建了一个箱线图。

我们可以看到在这个数据集上学习率大于 1.0 时模型性能下降的总体趋势。

AdaBoost 集成学习率与分类精度的箱线图

探索替代算法

集成中使用的默认算法是决策树，但也可以使用其他算法。

目的是使用非常简单的模型，称为弱学习器。此外，scikit-learn 实现要求使用的任何模型还必须支持加权样本，因为它们是通过基于训练数据集的加权版本拟合模型来创建集成的方式。

可以通过“ base_estimator ”参数指定基本模型。在分类的情况下，基础模型还必须支持预测概率或类概率分数。如果指定的模型不支持加权训练数据集，您将看到如下错误信息：

ValueError: KNeighborsClassifier doesn't support sample_weight.

支持加权训练的模型的一个示例是逻辑回归算法。

下面的例子演示了一个 AdaBoost 算法逻辑回归算法弱学习者。

# 评估 adaboost 算法与逻辑回归弱学习者的分类方法

from numpy import mean





# 定义模型

modl = AdaClass(est=Logi())

# 评估该模型

cv = ReaeSrfiedKd(nspis=10, neas=3, andm_=1)

sce =crsvlre(del, X, y, scrg='acacy', cv=cv, nos=-1, r_soe='ase')

# 报告性能

运行示例报告模型的均值和标准偏差准确度。

注意：考虑到算法或评估程序的随机性，或数值精度的差异。考虑多次运行该示例并比较平均结果。

在这种情况下，我们可以看到带有逻辑回归弱模型的 AdaBoost 集成在这个测试数据集上实现了大约 79% 的分类准确率。

网格搜索 AdaBoost 超参数

将 AdaBoost 配置为算法可能具有挑战性，因为影响模型在训练数据上的行为的许多关键超参数和超参数相互交互。

因此，使用搜索过程来发现对给定的预测建模问题运行良好或最佳的模型超参数配置是一种很好的做法。流行的搜索过程包括随机搜索和网格搜索。

在本节中，我们将研究 AdaBoost 算法的关键超参数的网格搜索通用范围，您可以将其用作您自己项目的起点。这可以通过使用_GridSearchCV_ 类并指定一个字典来实现，该字典将模型超参数名称映射到要搜索的值。

在这种情况下，我们将对 AdaBoost 的两个关键超参数进行网格搜索：集成中使用的树的数量和学习率。我们将为每个超参数使用一系列流行的表现良好的值。

将使用重复的 k 折交叉验证评估每个配置组合，并使用平均分数（在本例中为分类精度）比较配置。

下面列出了在我们的合成分类数据集上对 AdaBoost 算法的关键超参数进行网格搜索的完整示例。

# 在分类数据集上用网格搜索adaboost的关键超参数的例子

from sklearn.datasets import make_classification



# 定义数据集

X, y = mke( neares=0, nnrte=15, nednt=5, rd_sae=6)

# 用默认的超参数定义模型

mdl = AdaosCr()

# 定义要搜索的数值的网格
rid =ict()

gid\['n_estrs'\] = \[10, 50, 100, 500\] 

grd\['lri_at'\] = \[0.0001, 0.001, 0.01, 0.1, 1.0\] 

# 定义评估程序

cv = RaSteKld(n\_lts=10, n\_eet=3, rn_te=1)

# 定义网格搜索程序
gri\_arh = GiarcCV(ipostor=oel, pram\_ri=gid, n_os=-1, cv=cv, srg='auacy')

# 执行网格搜索

gr_ru = gr.fit(X, y)

# 总结最佳得分和配置


# 总结所有被评估过的分数



for man, sev,prm in zip(ansstds, pams):
    print(")wt:" mantdv, paam))

运行该示例可能需要一段时间。在运行结束时，首先报告获得最佳分数的配置，然后是考虑的所有其他配置的分数。

在这种情况下，我们可以看到具有 500 棵树和 0.1 学习率的配置表现最好，分类准确率约为 81.3%。

尽管在这种情况下没有测试这些配置以确保网格搜索在合理的时间内完成，但模型可能会在更多树（例如 1,000 或 5,000）下表现得更好。