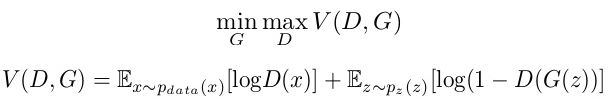小孩都看得懂的 GAN
全文共 6327 字,55 幅图,
预计阅读时间 32 分钟。
本文是「小孩都看得懂」系列的第十八篇,本系列的特点是内容不长,碎片时间完全可以看完,但我背后付出的心血却不少。喜欢就好!
小孩都看得懂的神经网络
小孩都看得懂的推荐系统
小孩都看得懂的逐步提升
小孩都看得懂的聚类
小孩都看得懂的主成分分析
小孩都看得懂的循环神经网络
小孩都看得懂的 Embedding
小孩都看得懂的熵、交叉熵和 KL 散度
小孩都看得懂的 p-value
小孩都看得懂的假设检验
小孩都看得懂的基尼不纯度
小孩都看得懂的 ROC
小孩都看得懂的 SVD
小孩都看得懂的 SVD 2
小孩都看得懂的 GMM
小孩都看得懂的贝塔分布
小孩都看得懂的多臂老虎机
小孩都看得懂的 GAN
0
GAN 是什么
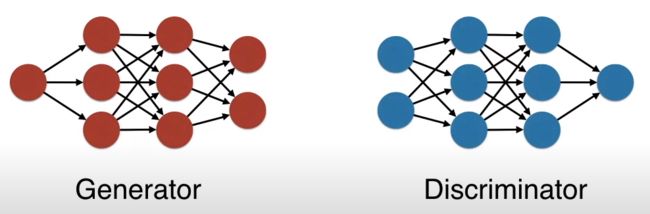
GAN 的全称是 Generative Adversarial Network,中文是生成对抗网络。
一言以蔽之,GAN 包含了两个神经网络,生成器(generator)和辨别器(discriminator),两者互相博弈不断变强,即生成器产出的东西越来越逼真,辨别器的识别能力越来越牛逼。
2
造假和鉴定
生成器和辨别器之间的关系很像造假者(counterfeiter)和鉴定者(Appraiser)之间的关系。
造假者不断造出假货,目的就是蒙骗鉴定者,在此过程中其造假能力越来越高。
鉴定者不断检验假货,目的就是识破造假者,在此过程中其鉴定能力越来越高。
GAN 是造假者的,也是鉴定者的,但归根结底还是造假者的。GAN 的最终目标是训练出一个“完美”的造假者,即能让生成让鉴定者都蒙圈的产品。
一动图胜千言,下图展示“造假者如何一步步生成逼真的蒙娜丽莎画而最终欺骗了鉴定者”的过程。
在此过程中,每当造假者生成一幅图。鉴定者会给出反馈,造假者从中学到如何改进来画出一张逼真图。
3
造假鉴定网络?
回到神经网络,造假者用生成器来建模,鉴定者用辨别器来建模。
根据上面动图可知,辨别器的任务是区分哪些图片是真实的,哪些图片是生成器产生的。
接下来我们用 Python 创建一个极简 GAN。
首先设置一个故事背景。
4
故事背景
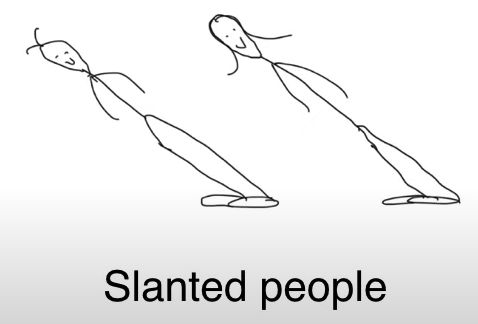
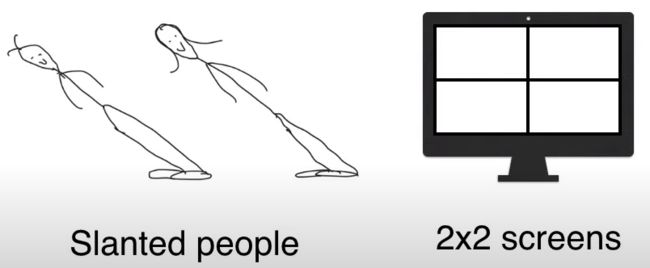
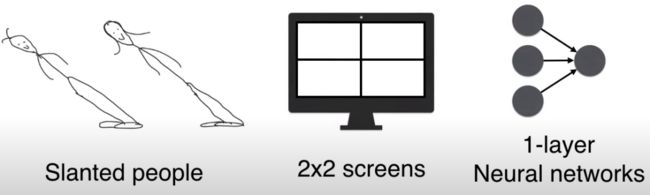
在倾斜岛(slanted island)上,每个人都是倾斜的,大概像左倾斜 45 度左右。
岛主想做人脸生成器,由于岛上的人的脸部特征非常简单,因此用 2 * 2 像素的模糊人脸图片。
限于技术,岛主只用了个一层的神经网络。
但在这个极度简单的设置下,一层的 GAN 也能生成“倾斜人脸”。
5
辨别人脸
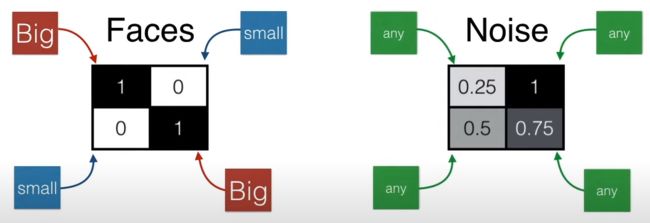
下图展示四个人脸的样子。
从 2*2 像素来表示人脸,深色代表此处有人脸,浅色代表此处没有人脸。
如果不是人脸呢?那么其 2*2 像素图中的元素就是随机的,如下所示。
复习一下:
人脸:对角线上是深色,非对角线上是浅色
非人脸:任意四处都可能是深色或浅色
像素可以用 0 到 1 的数值来表示:
人脸:对角线上的数值大,非对角线上的数值小
非人脸:任意四处都可能是 0-1 之间的任意数值
弄清了人脸照片和非人脸照片用不同特征的 2*2 数值矩阵表示之后,接下来两节我们来看如何构建辨别器(discriminator)和生成器(generator)。
先分析辨别器。
6
辨别器
辨别器就是用来辨别人脸,那么当看到照片的像素值时,如何辨别呢?
简单!上节已经分析过:
人脸:对角线上的数值大,非对角线上的数值小
非人脸:任意四处都可能是 0-1 之间的任意数值
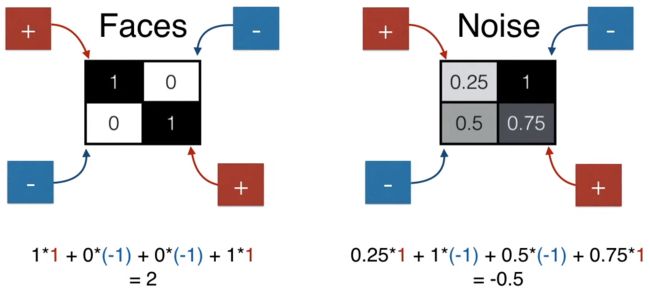
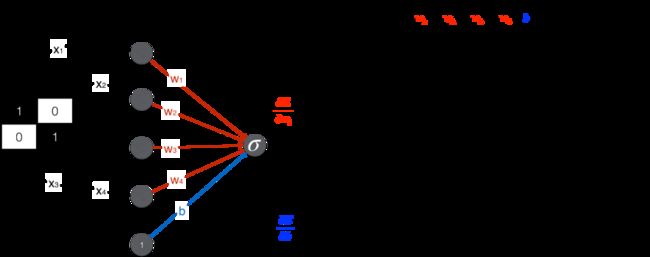
如果要用一个数值表示人脸和非人脸,该用什么样的操作呢?也简单,如下图所示,加上 (1,1) 位置的元素,减去 (1,2) 位置的元素,减去 (2,1) 位置的元素,加上 (2,2) 位置的元素,得到一个数值就可以了。
人脸得到的分数是 2(较大),非人脸得到的分数是 -0.5(较小)。
设定一个阈值 1,得分大于 1 是人脸,小于 1 不是人脸。
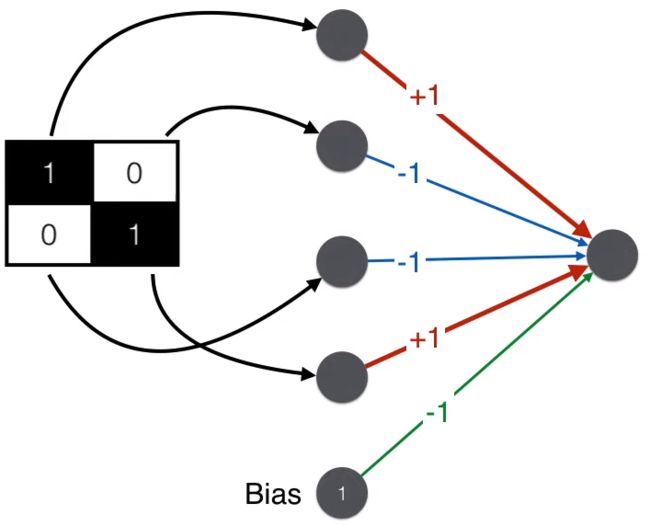
将上述内容用神经网络来表示,就成了下面的极简辨别器了。注意除了“加减减加”矩阵 4 个元素之外,最后还加上一个偏置项(bias)得到最终得分。
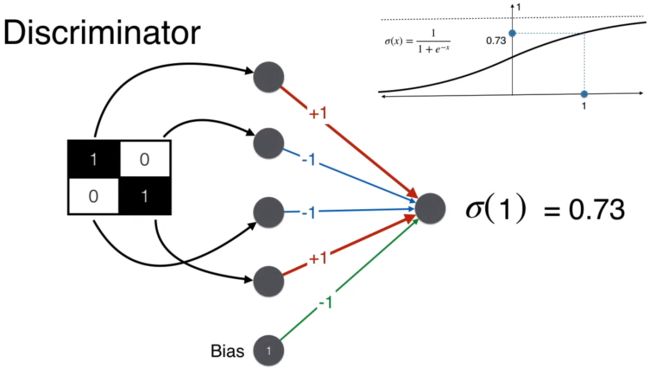
辨别器最终要判断是否是人脸,因此产出是一个概率,需要用 sigmoid 函数将得分 1 转化成概率 0.73。给定概率阈值 0.5,由于 0.73 > 0.5,辨别器判断该图是人脸。
对另一张非人脸的图,用同样操作,最后算出得分 -0.5,用 sigmoid 函数转换。给定概率阈值 0.5,由于 0.37 < 0.5,辨别器判断该图是人脸。
7
生成器
辨别器目标是判断人脸。而生成器目标是生成人脸,那什么样的矩阵像素是人脸图呢?简单!该规则被已经分析多次了:
人脸:对角线上的数值大,非对角线上的数值小
非人脸:任意四处都可能是 0-1 之间的任意数值
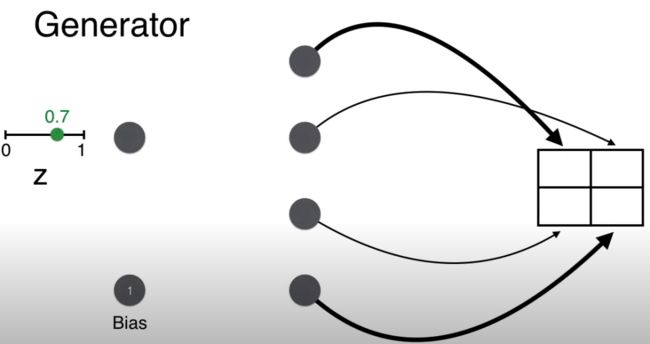
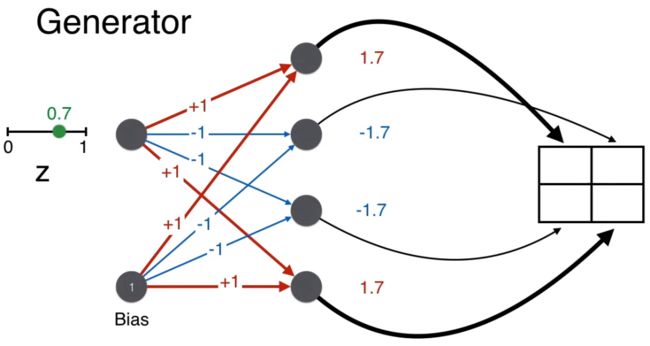
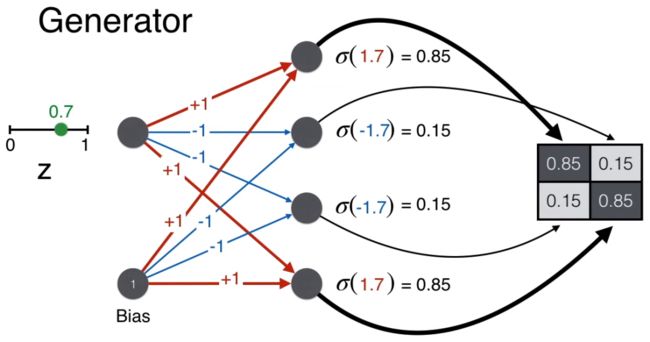
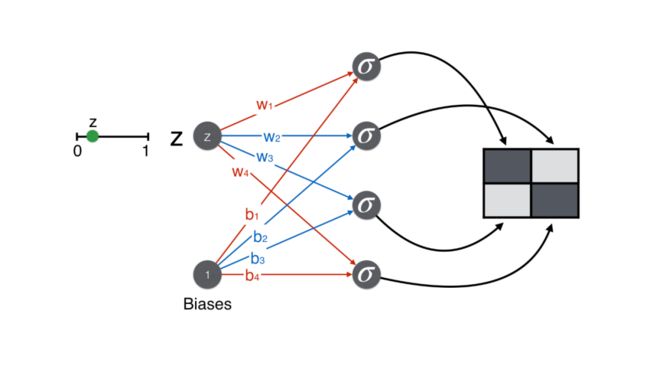
现在来看生成过程。第一步就是从 0-1 之间随机选取一个数,比如 0.7。
回忆生成器的目的是生成人脸,即要保证最终 2*2 矩阵的对角线上的像素要大(用粗线表明),而非对角线上的像素要小(用细线表明)。
举例,生成矩阵 (1,1) 位置的值,w = 1, b = 1,计算的分 wz + b = 1.7。
同理计算矩阵其他三个位置的得分。
最后都用 sigmoid 函数将得分转换一下,确保像素值在 0-1 之间。
注意按上图这样给权重 [1, -1, -1, 1] 和偏置 1,有因为 z 总是在 0 和 1 之间的一个正数,这样的一个神经网络(生成器)总可以生成一个像人脸的 2*2 的像素矩阵。
根据本节和上节的展示,我们已经知道什么样的辨别器可以判断人脸,什么样的生成器可以生成好的人脸,即什么样的 GAN 是个好 GAN。这些都是由权重和偏置决定的,接下来看看它们是怎么训练出来的。首先复习一下误差函数(error function)。
8
误差函数
通常把正类用 1 表示,负类用 0 表示。在本例中人脸是正类,用 1 表示;非人脸是负类,用 0 表示。
当标签为 1 时(人脸),-ln(x) 是一个好的误差函数,因为
当预测不准时(预测非人脸,假设 0.1),那么误差应该较大,- ln(0.1) 较大。
当预测准时(预测人脸,假设 0.9),那么误差应该较小,-ln(0.9) 较小。
当标签为 0 时(非人脸),-ln(1-x) 是一个好的误差函数。
当预测准时(预测非人脸,假设 0.1),那么误差应该较小,- ln(1-0.1) 较大。
当预测不准时(预测人脸,假设 0.9),那么误差应该较大,-ln(1-0.9) 较小。
根据下面两张总结图再巩固一下 ln 函数作为误差函数的逻辑。
接下来就是 GAN 中博弈,即生成器和辨别器放在一起会发生什么事情。
9
生成器和辨别器放在一起
复习一下两者的结构。
生成器:输入是一个 0-1 之间的随机数,输出是图片的像素矩阵
辨别器:输入是图片像素矩阵,输出是一个概率值
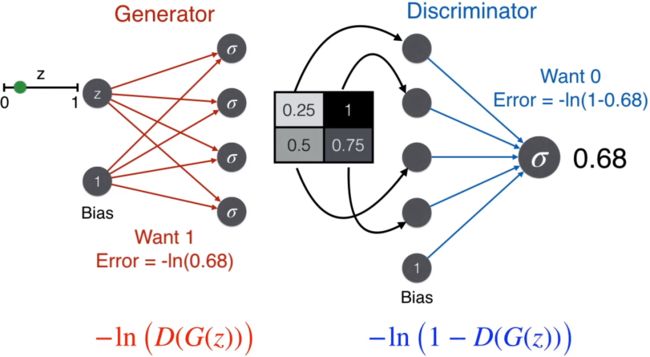
下面动图展示了从生成器到辨别器的流程。
因为该图片是从生成器来的,不是真实图片,因此一个好的辨别器会判断这不是脸,那么使用标签为 0 对应的误差函数,-ln(1-prediction)。
反过来,一个好的生成器想骗过辨别器,即想让辨别器判断这是脸,那么使用标签为 1 对应的误差函数,-ln(prediction)。
好戏来了,用 G 表示生成器,D 表示辨别器,那么
G(z) 是生成器的产出,即像素矩阵,它也是辨别器的输入
D(G(z)) 是辨别器的产出,即概率,又是上面误差函数里的 prediction
为了使生成器和辨别器都变强,我们希望最小化误差函数
-ln(D(G(z)) - ln(1-D(G(z))
其中 D(G(z)) 就是辨别器的 prediction。
将我们得到的误差函数对比 GAN 论文中的目标函数(下图),发现还是有些差别:
解释如下:
辨别器除了接收生成器产出的图片 G(z),还会接收真实图片 x,在这时一个好的辨别器会判断这是脸,那么使用标签为 1 对应的误差函数,-ln(-prediction)。那么对于辨别器,需要最小化的误差函数是
-ln(D(x)) - ln(1-D(G(z))
将负号去掉,等价于最大化
ln(D(x)) + ln(1-D(G(z))
这个不就是 V(D,G) 么?此过程是固定生成器,来优化辨别器来识别假图片。
V(D, G) 最大化后,在固定辨别器,来优化生成器来生成以假乱真的图片。但是生成器的误差函数不是 -ln(D(G(z)) 吗?怎么能和 V(D, G) 扯上关系呢?其实 -ln(D(G(z)) 等价于 ln(1-D(G(z)),这时 V(D, G) 的第二项,而其第一项 ln(D(x)) 对于 G 是个常数,加不加都无所谓。
最后 V(D, G) 中的两项都有期望符号,在实际优化中我们就通过 n 个样本的统计平均值来实现。第一项期望中的 x 从真实数据分布 p_data(x) 中来,第一项期望中的 z 从特定概率分布 p_z(z) 中来。
综上,先通过 D 最大化 V(D,G) 再通过 G 最小化 V(D, G)。
10
训练 GAN
在训练中,当人脸来自生成器,通过最小化误差函数,辨别器输出概率值接近 0。
当人脸来自真实图片,通过最小化误差函数,辨别器输出概率值接近 1。
当然所有神经网络的训练算法都是梯度下降了。
OK,接下来的内容确实不适合普通小孩了,对数学和编程有强烈兴趣的小孩可以继续看下去  。
。
11
数学推导
辨别器:从像素矩阵到概率
生成器:从随机数 z 到像素矩阵
得到误差函数相对于生成器和辨别器中的权重和偏置的各种偏导数后,就可以写代码实现了。
12
Python 实现 - 准备工作
引入 numpy 和 matplotlib。
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline编写绘画人脸像素的函数。
def view_samples(samples, m, n):
fig, axes = plt.subplots(figsize=(10, 10),
nrows=m, ncols=n,
sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples):
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(1-img.reshape((2,2)), cmap='Greys_r')
return fig, axes画出四张人脸,注意其像素矩阵中对角线上的数值大,非对角线上的数值小。
faces = [np.array([1,0,0,1]),
np.array([0.9,0.1,0.2,0.8]),
np.array([0.9,0.2,0.1,0.8]),
np.array([0.8,0.1,0.2,0.9]),
np.array([0.8,0.2,0.1,0.9])]
_ = view_samples(faces, 1, 4)画出二十张非人脸,注意其像素矩阵中的数都是随机的。
noise = [np.random.randn(2,2) for i in range(20)]
def generate_random_image():
return [np.random.random(), np.random.random(), np.random.random(), np.random.random()]
_ = view_samples(noise, 4,5)13
Python 实现 - 构建辨别器
首先实现 sigmoid 函数。
def sigmoid(x):
return np.exp(x)/(1.0+np.exp(x))用面向对象编程(OOP)来编写辨别器,代码如下:
其中
__init__() 是构建函数
forward() 函数将像素矩阵打平成向量 x,乘上权重 w 加上偏置 b 得到得分,再通过 sigmoid() 函数转成概率
error_form_image() 计算当接收真实图片为输入的误差函数
error_form_noise() 计算当接收生成器为输入的误差函数
derivatives_form_image() 计算当接收真实图片为输入误差函数对权重 w 和偏置 b 的偏导数
derivatives_form_noise() 计算当接收生成器为输入误差函数对权重 w 和偏置 b 的偏导数
update_form_image() 计算当接收真实图片为输入时的梯度下降法
update_form_noise() 计算当接收生成器为输入时的梯度下降法
14
Python 实现 - 构建生成器
用面向对象编程(OOP)来编写生成器,代码如下:
其中
__init__() 是构建函数
forward() 函数将随机数 z 乘上权重 w 加上偏置 b 得到得分,再通过 sigmoid() 函数转成像素
error() 计算当固定辨别器为输入的误差函数,分两步:
生成器的 forward() 函数得到像素
辨别器的 forward() 函数得到概率
derivatives() 计算当固定辨别器为输入误差函数对权重 w 和偏置 b 的偏导数,对着上一节数学公式看代码
update() 计算当固定辨别器为输入时的梯度下降法
15
Python 实现 - 训练 GAN
设定 1000 期(epoch),即将数据遍历 1000 遍开始训练,记录每期生成器和辨别器的误差。
画出生成器和辨别器的误差函数图,发现生成器逐步趋于稳定。
plt.plot(errors_generator)
plt.title("Generator error function")
plt.legend("gen")
plt.show()
plt.plot(errors_discriminator)
plt.legend('disc')
plt.title("Discriminator error function")16
Python 实现 - 结果展示
生成图片。
generated_images = []
for i in range(4):
z = random.random()
generated_image = G.forward(z)
generated_images.append(generated_image)
_ = view_samples(generated_images, 1, 4)
for i in generated_images:
print(i)[0.94688171 0.03401213 0.04080795 0.96308679]
[0.95653992 0.03437852 0.03579494 0.97063836]
[0.95056667 0.03414339 0.03893305 0.96599501]
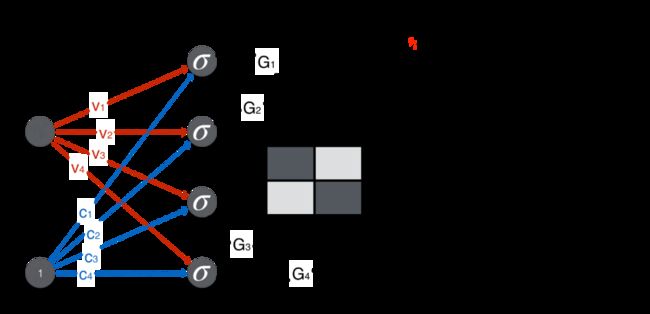
[0.94228203 0.03386046 0.04309146 0.95941292]打印出最终 GAN 的参数,即生成器和辨别器的权重和偏置。
print("Generator weights", G.weights)
print("Generator biases", G.biases)
print("Discriminator weights", D.weights)
print("Discriminator bias", D.bias)Generator weights [ 0.70702123 0.03720449 -0.45703394 0.79375751]
Generator biases [ 2.48490157 -3.36725912 -2.90139211 2.8172726 ]
Discriminator weights [ 0.60175083 -0.29127513 -0.40093314 0.37759987]
Discriminator bias -0.8955103005797729带有权重和偏置的 GAN 如下所示。
图中粗线对应大权重,细线对应小或者负权重。对照前面生成器要生成逼真人脸的目标来看(即 2*2 矩阵的对角线上的值大),是不是这个权重很合理。
朋友们,你们弄懂了 GAN 了吗?
想学习 Python 内容,可参考我的《三套 Python 精品课》。