吴恩达《神经网络和深度学习》第四周编程作业—深度神经网络应用--Cat or Not?
吴恩达《神经网络和深度学习》— 深度神经网络应用--Cat or Not?
- 1 安装包
- 2 数据集
- 3 模型的结构
-
- 3.1 两层神经网络
- 3.2 L层深度神经网络
- 3.3 通用步骤
- 4 两层神经网络
- 5 L层神经网络
- 6 结果分析
- 7 使用自己的图像进行测试
- 8 完整代码
※※※※※上一篇:【构建深度神经网络】※※※※※
在这篇文章中,我们将使用在上一篇文章中实现的函数来构建深层网络,并将其应用于分类cat图像和非cat图像。希望你会看到相对于先前的逻辑回归实现的分类,准确性有所提高。
学完本篇文章将掌握的技能:
∙ \bullet ∙ 建立深度神经网络并将其应用于监督学习
本文所使用的资料:【点击下载】,提取码:hwwc。请在开始之前下载好所需资料,然后将文件解压到你的代码文件同一级目录下,请确保你的代码那里有dnn_utils.py、testCases.py 、 lr_utils.py 文件以及一个包含数据集的文件夹datasets。
1 安装包
【说明】:在阅读这篇文章之前,请先阅读上一篇文章构建深度神经网络。博主把上篇文章中创建的所有函数都存放在一个名为dnn_app_utils.py的文件中(源代码可以参见本文本末),并且将在本篇文章中导入。
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils import *
from lr_utils import load_dataset
2 数据集
在这里,我们将使用与“用神经网络思想实现Logistic回归”中相同的“cats vs non-cats”数据集。此前建立的模型在对猫和非猫图像进行分类时只有70%的准确率。我们来看看利用深度神经网络模型,分类的准确性能不能得到提高。
【说明】:在文件夹datasets下包含两个数据集:训练集(train_catvnoncat.h5)和 测试集(test_catvnoncat.h5)。
∙ \bullet ∙ 标记为cat(1)和non-cat(0)图像的训练集m_train
∙ \bullet ∙ 标记为cat(1)和non-cat(0)图像的测试集m_test
∙ \bullet ∙ 每个图像的维度都为(num_px,num_px,3),其中3表示3个通道(RGB)。
让我们熟悉一下数据集吧, 首先通过运行以下代码来加载数据。
train_x_orig, train_y, test_x_orig, test_y, classes = load_dataset()
运行以下代码以展示数据集中的图像。通过更改索引,然后重新运行单元以查看其他图像。
【代码】:
# Example of a picture
index = 7
print("y = " + str(train_y[0, index]) + ". It's a " + classes[train_y[0, index]].decode("utf-8") + " picture.")
plt.imshow(train_x_orig[index])
plt.show()
【运行结果】:
y = 1. It's a cat picture.
通过以下代码可以查看训练集和测试集数据的具体信息。
【代码】:
# Explore your dataset
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]
print("Number of training examples: " + str(m_train))
print("Number of testing examples: " + str(m_test))
print("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print("train_x_orig shape: " + str(train_x_orig.shape))
print("train_y shape: " + str(train_y.shape))
print("test_x_orig shape: " + str(test_x_orig.shape))
print("test_y shape: " + str(test_y.shape))
【运行结果】:
Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)
与往常一样,在将图像输入到网络之前,需要对图像进行重塑和标准化。如下图所示:

【代码】:
# Reshape the training and test examples
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T
# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.
print("train_x's shape: " + str(train_x.shape))
print("test_x's shape: " + str(test_x.shape))
【运行结果】:
train_x's shape: (12288, 209)
test_x's shape: (12288, 50)
【说明】: 12288 = 64 × 64 × 3 12288 = 64 \times 64 \times 3 12288=64×64×3,这是图像重塑为向量的大小。
3 模型的结构
接下来,我们将建立两个不同的模型:
∙ \bullet ∙ 两层神经网络
∙ \bullet ∙ L层深度神经网络
然后,我们将比较这些模型的性能,并尝试不同的值。
3.1 两层神经网络
该模型可以总结为:INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT
对于一个样本,具体实现步骤为:
∙ \bullet ∙ 输入维度为 ( 64 , 64 , 3 ) (64, 64, 3) (64,64,3) 的图像,将其展平为大小为 ( 12288 , 1 ) (12288, 1) (12288,1) 的向量。
∙ \bullet ∙ 相应的向量: [ x 0 , x 1 , ⋯ , x 12287 ] T \left [ x_{0}, x_{1},\cdots ,x_{12287} \right ]^{T} [x0,x1,⋯,x12287]T 乘以大小为 ( n [ 1 ] , 12288 ) \left ( n^{\left [ 1 \right ]},12288 \right ) (n[1],12288) 的权重矩阵 W [ 1 ] W^{\left [ 1 \right ]} W[1]。
∙ \bullet ∙ 然后添加一个偏差项并按照公式获得以下向量: [ a 0 [ 1 ] , a 1 [ 1 ] , ⋯ , a n [ 1 ] − 1 [ 1 ] ] T \left [ a_{0}^{\left [ 1 \right ]},a_{1}^{\left [ 1 \right ]},\cdots ,a_{n^{\left [ 1 \right ]}-1}^{\left [ 1 \right ]} \right ]^{T} [a0[1],a1[1],⋯,an[1]−1[1]]T。
∙ \bullet ∙ 然后,重复相同的过程。
∙ \bullet ∙ 将所得向量乘以 W [ 2 ] W^{\left [ 2 \right ]} W[2] 并加上截距(偏差)。
∙ \bullet ∙ 最后,采用结果的sigmoid值。如果大于0.5,则将其分类为猫。
3.2 L层深度神经网络
该模型可以总结为:[LINEAR -> RELU] x (L-1) -> LINEAR -> SIGMOID
对于一个样本,具体实现步骤为:
∙ \bullet ∙ 输入维度为 ( 64 , 64 , 3 ) (64, 64, 3) (64,64,3) 的图像,将其展平为大小为 ( 12288 , 1 ) (12288, 1) (12288,1) 的向量。
∙ \bullet ∙ 相应的向量: [ x 0 , x 1 , ⋯ , x 12287 ] T \left [ x_{0}, x_{1},\cdots ,x_{12287} \right ]^{T} [x0,x1,⋯,x12287]T 乘以大小为 ( n [ 1 ] , 12288 ) \left ( n^{\left [ 1 \right ]},12288 \right ) (n[1],12288) 的权重矩阵 W [ 1 ] W^{\left [ 1 \right ]} W[1],然后加上截距 b [ 1 ] b^{\left [ 1 \right ]} b[1],结果为线性单元。
∙ \bullet ∙ 接下来计算获得的线性单元的Relu值。
∙ \bullet ∙ 把得到的激活值乘以大小为 ( n [ 2 ] , n [ 1 ] ) \left ( n^{\left [ 2 \right ]},n^{\left [ 1 \right ]} \right ) (n[2],n[1]) 的权重矩阵 W [ 1 ] W^{\left [ 1 \right ]} W[1],然后加上截距 b [ 2 ] b^{\left [ 2 \right ]} b[2],结果为线性单元。
∙ \bullet ∙ 接下来计算获得的线性单元的Relu值。
∙ \bullet ∙ 重复上述步骤 (L-1) 次。
∙ \bullet ∙ 最后,采用最终线性单位的sigmoid值。如果大于0.5,则将其分类为猫。
3.3 通用步骤
构建深度神经网络模型的一般步骤如下:
1. 初始化参数/定义超参数
2. 循环num_iterations次:
∙ \bullet ∙ 正向传播
∙ \bullet ∙ 计算损失函数
∙ \bullet ∙ 反向传播
∙ \bullet ∙ 更新参数(使用参数和反向传播的梯度)
3. 使用训练好的参数来预测标签
4 两层神经网络
使用上一篇文章构建深度神经网络中实现的辅助函数来构建具有以下结构的两层神经网络:LINEAR -> RELU -> LINEAR -> SIGMOID,你可能需要的函数及其输入为:
def initialize_parameters(n_x, n_h, n_y):
...
return parameters
def linear_activation_forward(A_prev, W, b, activation):
...
return A, cache
def compute_cost(AL, Y):
...
return cost
def linear_activation_backward(dA, cache, activation):
...
return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
...
return parameters
【代码】:
# GRADED FUNCTION: two_layer_model
def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
"""
Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (n_x, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- dimensions of the layers (n_x, n_h, n_y)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- If set to True, this will print the cost every 100 iterations
Returns:
parameters -- a dictionary containing W1, W2, b1, and b2
"""
np.random.seed(1)
grads = {
}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
(n_x, n_h, n_y) = layers_dims
# Initialize parameters dictionary, by calling one of the functions you'd previously implemented
parameters = initialize_parameters(n_x, n_h, n_y)
# Get W1, b1, W2 and b2 from the dictionary parameters.
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID.
# Inputs: "X, W1, b1".
# Output: "A1, cache1, A2, cache2".
A1, cache1 = linear_activation_forward(X, W1, b1, activation="relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, activation="sigmoid")
# Compute cost
cost = compute_cost(A2, Y)
# Initializing backward propagation
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
# Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation="sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation="relu")
# Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Retrieve W1, b1, W2, b2 from parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
现在可以正式开始训练了。
【代码】:
# CONSTANTS DEFINING THE MODEL
n_x = 12288 # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
parameters = two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), num_iterations=2500, print_cost=True)
【运行结果】:
Cost after iteration 0: 0.693049735659989
Cost after iteration 100: 0.6464320953428849
Cost after iteration 200: 0.6325140647912677
Cost after iteration 300: 0.6015024920354665
Cost after iteration 400: 0.5601966311605747
Cost after iteration 500: 0.5158304772764729
Cost after iteration 600: 0.47549013139433255
Cost after iteration 700: 0.4339163151225749
Cost after iteration 800: 0.40079775362038894
Cost after iteration 900: 0.35807050113237987
Cost after iteration 1000: 0.33942815383664127
Cost after iteration 1100: 0.3052753636196264
Cost after iteration 1200: 0.27491377282130164
Cost after iteration 1300: 0.24681768210614832
Cost after iteration 1400: 0.19850735037466102
Cost after iteration 1500: 0.17448318112556652
Cost after iteration 1600: 0.1708076297809593
Cost after iteration 1700: 0.11306524562164731
Cost after iteration 1800: 0.09629426845937145
Cost after iteration 1900: 0.08342617959726863
Cost after iteration 2000: 0.07439078704319081
Cost after iteration 2100: 0.06630748132267927
Cost after iteration 2200: 0.05919329501038169
Cost after iteration 2300: 0.05336140348560552
Cost after iteration 2400: 0.04855478562877016
迭代完成之后我们就可以进行预测了,预测函数如下:
【代码】:
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 测试集标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1, m))
# 根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("准确度为: " + str(float(np.sum((p == y)) / m)))
return p
预测函数构建好了我们就开始预测,查看训练集和测试集的准确性:
【代码】:
predictions_train = predict(train_x, train_y, parameters) # 训练集
predictions_test = predict(test_x, test_y, parameters) # 测试集
【运行结果】:
准确度为: 1.0
准确度为: 0.72
从上述结果可以看出,两层神经网络的性能(72%)比逻辑回归实现(70%)更好。接下来,让我们看看使用 L L L 层神经网络模型是否可以做得更好。
5 L层神经网络
【代码】:
# GRADED FUNCTION: L_layer_model
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False): # lr was 0.009
"""
Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
Arguments:
X -- data, numpy array of shape (number of examples, num_px * num_px * 3)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
learning_rate -- learning rate of the gradient descent update rule
num_iterations -- number of iterations of the optimization loop
print_cost -- if True, it prints the cost every 100 steps
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(1)
costs = [] # keep track of cost
# Parameters initialization.
parameters = initialize_parameters_deep(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
AL, caches = L_model_forward(X, parameters)
# Compute cost.
cost = compute_cost(AL, Y)
# Backward propagation.
grads = L_model_backward(AL, Y, caches)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration %i: %f" % (i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
现在,让我们训练5层的神经网络模型。
【代码】:
layers_dims = [12288, 20, 7, 5, 1] # 5-layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations=2500, print_cost=True)
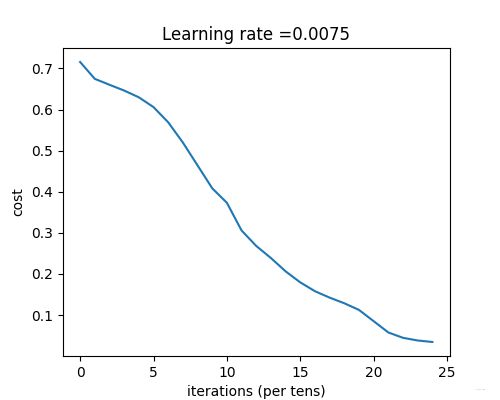
【运行结果】:
Cost after iteration 0: 0.715732
Cost after iteration 100: 0.674738
Cost after iteration 200: 0.660337
Cost after iteration 300: 0.646289
Cost after iteration 400: 0.629813
Cost after iteration 500: 0.606006
Cost after iteration 600: 0.569004
Cost after iteration 700: 0.519797
Cost after iteration 800: 0.464157
Cost after iteration 900: 0.408420
Cost after iteration 1000: 0.373155
Cost after iteration 1100: 0.305724
Cost after iteration 1200: 0.268102
Cost after iteration 1300: 0.238725
Cost after iteration 1400: 0.206323
Cost after iteration 1500: 0.179439
Cost after iteration 1600: 0.157987
Cost after iteration 1700: 0.142404
Cost after iteration 1800: 0.128652
Cost after iteration 1900: 0.112443
Cost after iteration 2000: 0.085056
Cost after iteration 2100: 0.057584
Cost after iteration 2200: 0.044568
Cost after iteration 2300: 0.038083
Cost after iteration 2400: 0.034411
训练完成,我们看一下预测:
【代码】:
predictions_train = predict(train_x, train_y, parameters) # 训练集
predictions_test = predict(test_x, test_y, parameters) # 测试集
【预测结果】:
准确度为: 0.9952153110047847
准确度为: 0.78
就准确度而言,从70%到72%再到78%,可以看到的是准确度在一点点增加,当然,你也可以手动的去调整layer_dims,准确度可能又会提高一些。
6 结果分析
我们可以看一看有哪些东西在L层模型中被错误地标记了,导致准确率没有提高。
【代码】:
def print_mislabeled_images(classes, X, y, p):
"""
绘制预测和实际不同的图像。
X - 数据集
y - 实际的标签
p - 预测
"""
a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))
plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
num_images = len(mislabeled_indices[0])
for i in range(num_images):
index = mislabeled_indices[1][i]
plt.subplot(2, num_images // 2 + 1, i + 1)
plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
plt.axis('off')
plt.title("Prediction: " + classes[int(p[0, index])].decode("utf-8") + " \n Class: " + classes[y[0, index]].decode("utf-8"))
plt.show()
print_mislabeled_images(classes, test_x, test_y, predictions_test)
根据上述结果,我们可以总结出模型往往表现欠佳的几种类型的图像包括:
∙ \bullet ∙ 猫身处于异常位置
∙ \bullet ∙ 图片背景与猫颜色类似
∙ \bullet ∙ 猫的种类和颜色稀有
∙ \bullet ∙ 相机角度
∙ \bullet ∙ 图片的亮度
∙ \bullet ∙ 比例变化(猫的图像很大或很小)
7 使用自己的图像进行测试
【说明】:
在使用自己的图像进行测试前,需要完成以下准备工作:
∙ \bullet ∙ 将图像添加到包含数据集的文件夹datasets中。
∙ \bullet ∙ 在以下代码中更改图像的路径及名称。
∙ \bullet ∙ 运行代码,检查算法是否正确(1 = cat,0 = non-cat)!
【代码】:
my_image = "datasets/cat.jpg" # change this to the name of your image file
my_label_y = [1] # the true class of your image (1 -> cat, 0 -> non-cat)
fname = my_image
image = np.array(plt.imread(fname))
my_image = np.array(Image.fromarray(image).resize(size=(num_px, num_px))).reshape((num_px*num_px*3, 1))
my_predicted_image = predict(my_image, my_label_y, parameters)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" +
classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
plt.show()
当输入为一张猫的图像,如下图所示:
准确度为: 1.0
y = 1.0, your L-layer model predicts a "cat" picture.
准确度为: 1.0
y = 0.0, your L-layer model predicts a "non-cat" picture.
【结果】:
准确度为: 1.0
y = 0.0, your L-layer model predicts a "non-cat" picture.
8 完整代码
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils import *
from lr_utils import load_dataset
np.random.seed(1)
train_x_orig, train_y, test_x_orig, test_y, classes = load_dataset()
# # Example of a picture
# index = 7
# print("y = " + str(train_y[0, index]) + ". It's a " + classes[train_y[0, index]].decode("utf-8") + " picture.")
# plt.imshow(train_x_orig[index])
# plt.show()
# Explore your dataset
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]
# print("Number of training examples: " + str(m_train))
# print("Number of testing examples: " + str(m_test))
# print("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
# print("train_x_orig shape: " + str(train_x_orig.shape))
# print("train_y shape: " + str(train_y.shape))
# print("test_x_orig shape: " + str(test_x_orig.shape))
# print("test_y shape: " + str(test_y.shape))
# Reshape the training and test examples
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T
# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.
# print("train_x's shape: " + str(train_x.shape))
# print("test_x's shape: " + str(test_x.shape))
# GRADED FUNCTION: two_layer_model
def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
"""
Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (n_x, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- dimensions of the layers (n_x, n_h, n_y)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- If set to True, this will print the cost every 100 iterations
Returns:
parameters -- a dictionary containing W1, W2, b1, and b2
"""
np.random.seed(1)
grads = {
}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
(n_x, n_h, n_y) = layers_dims
# Initialize parameters dictionary, by calling one of the functions you'd previously implemented
parameters = initialize_parameters(n_x, n_h, n_y)
# Get W1, b1, W2 and b2 from the dictionary parameters.
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID.
# Inputs: "X, W1, b1".
# Output: "A1, cache1, A2, cache2".
A1, cache1 = linear_activation_forward(X, W1, b1, activation="relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, activation="sigmoid")
# Compute cost
cost = compute_cost(A2, Y)
# Initializing backward propagation
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
# Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation="sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation="relu")
# Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Retrieve W1, b1, W2, b2 from parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
# GRADED FUNCTION: L_layer_model
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False): # lr was 0.009
"""
Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
Arguments:
X -- data, numpy array of shape (number of examples, num_px * num_px * 3)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
learning_rate -- learning rate of the gradient descent update rule
num_iterations -- number of iterations of the optimization loop
print_cost -- if True, it prints the cost every 100 steps
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(1)
costs = [] # keep track of cost
# Parameters initialization.
parameters = initialize_parameters_deep(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
AL, caches = L_model_forward(X, parameters)
# Compute cost.
cost = compute_cost(AL, Y)
# Backward propagation.
grads = L_model_backward(AL, Y, caches)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration %i: %f" % (i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 测试集标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1, m))
# 根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("准确度为: " + str(float(np.sum((p == y)) / m)))
return p
# # CONSTANTS DEFINING THE MODEL
# n_x = 12288 # num_px * num_px * 3
# n_h = 7
# n_y = 1
# layers_dims = (n_x, n_h, n_y)
# parameters = two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), num_iterations=2500, print_cost=True)
layers_dims = [12288, 20, 7, 5, 1] # 5-layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations=2500, print_cost=True)
# predictions_train = predict(train_x, train_y, parameters) # 训练集
# predictions_test = predict(test_x, test_y, parameters) # 测试集
def print_mislabeled_images(classes, X, y, p):
"""
绘制预测和实际不同的图像。
X - 数据集
y - 实际的标签
p - 预测
"""
a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))
plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
num_images = len(mislabeled_indices[0])
for i in range(num_images):
index = mislabeled_indices[1][i]
plt.subplot(2, num_images // 2 + 1, i + 1)
plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
plt.axis('off')
plt.title("Prediction: " + classes[int(p[0, index])].decode("utf-8") + " \n Class: " + classes[y[0, index]].decode("utf-8"))
plt.show()
# print_mislabeled_images(classes, test_x, test_y, predictions_test)
my_image = "datasets/girl.jpeg" # change this to the name of your image file
my_label_y = [0] # the true class of your image (1 -> cat, 0 -> non-cat)
fname = my_image
image = np.array(plt.imread(fname))
size = (num_px, num_px, 3)
my_image = np.resize(image, size).reshape((1, num_px*num_px*3)).T # 重置原始图片的大小
# my_image = np.array(Image.fromarray(image).resize(size=(num_px, num_px))).reshape((num_px*num_px*3, 1))
my_predicted_image = predict(my_image, my_label_y, parameters)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" +
classes[int(np.squeeze(my_predicted_image)), ].decode("utf-8") + "\" picture.")
plt.show()
【dnn_app_utils.py】:
import numpy as np
import h5py
import matplotlib.pyplot as plt
import testCases # 参见资料包
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward # 参见资料包
import lr_utils # 参见资料包
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
np.random.seed(1)
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
parameters -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(1)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
# # 测试initialize_parameters
# print("==============测试initialize_parameters==============")
# parameters = initialize_parameters(3, 2, 1)
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))
# GRADED FUNCTION: initialize_parameters_deep
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(3)
parameters = {
}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) / np.sqrt(layer_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert (parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
assert (parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
# # 测试initialize_parameters_deep
# print("==============测试initialize_parameters_deep==============")
# layers_dims = [5, 4, 3]
# parameters = initialize_parameters_deep(layers_dims)
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))
# GRADED FUNCTION: linear_forward
def linear_forward(A, W, b):
"""
Implement the linear part of a layer's forward propagation.
Arguments:
A -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
Returns:
Z -- the input of the activation function, also called pre-activation parameter
cache -- a python dictionary containing "A", "W" and "b" ; stored for computing the backward pass efficiently
"""
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
# # 测试linear_forward
# print("==============测试linear_forward==============")
# A, W, b = testCases.linear_forward_test_case()
# Z, linear_cache = linear_forward(A, W, b)
# print("A = " + str(A))
# print("W = " + str(W))
# print("b = " + str(b))
# print("Z = " + str(Z))
# GRADED FUNCTION: linear_activation_forward
def linear_activation_forward(A_prev, W, b, activation):
"""
Implement the forward propagation for the LINEAR->ACTIVATION layer
Arguments:
A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
A -- the output of the activation function, also called the post-activation value
cache -- a python dictionary containing "linear_cache" and "activation_cache";
stored for computing the backward pass efficiently
"""
if activation == "sigmoid":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
# # 测试linear_activation_forward
# print("==============测试linear_activation_forward==============")
# A_prev, W, b = testCases.linear_activation_forward_test_case()
# print("A_prev = " + str(A_prev))
# print("W = " + str(W))
# print("b = " + str(b))
#
# A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation="sigmoid")
# print("sigmoid,A = " + str(A))
#
# A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation="relu")
# print("ReLU,A = " + str(A))
# GRADED FUNCTION: L_model_forward
def L_model_forward(X, parameters):
"""
Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
Arguments:
X -- data, numpy array of shape (input size, number of examples)
parameters -- output of initialize_parameters_deep()
Returns:
AL -- last post-activation value
caches -- list of caches containing:
every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2)
the cache of linear_sigmoid_forward() (there is one, indexed L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)],
activation="relu")
caches.append(cache)
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation="sigmoid")
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
return AL, caches
# # 测试L_model_forward
# print("==============测试L_model_forward==============")
# X, parameters = testCases.L_model_forward_test_case()
# AL, caches = L_model_forward(X, parameters)
# print("X = " + str(X))
# print("parameters = " + str(parameters))
# print("AL = " + str(AL))
# print("caches 的长度为 = " + str(len(caches)))
# print("caches = " + str(caches))
# GRADED FUNCTION: compute_cost
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
cost = -1 / m * np.sum(Y * np.log(AL) + (1 - Y) * np.log(1 - AL), axis=1, keepdims=True)
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert (cost.shape == ())
return cost
# # 测试compute_cost
# print("==============测试compute_cost==============")
# Y, AL = testCases.compute_cost_test_case()
# print("Y = " + str(Y))
# print("AL = " + str(AL))
# print("cost = " + str(compute_cost(AL, Y)))
# GRADED FUNCTION: linear_backward
def linear_backward(dZ, cache):
"""
Implement the linear portion of backward propagation for a single layer (layer l)
Arguments:
dZ -- Gradient of the cost with respect to the linear output (of current layer l)
cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
A_prev, W, b = cache
m = A_prev.shape[1]
dW = 1 / m * np.dot(dZ, A_prev.T)
db = 1 / m * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
# # 测试linear_backward
# print("==============测试linear_backward==============")
# dZ, linear_cache = testCases.linear_backward_test_case()
#
# dA_prev, dW, db = linear_backward(dZ, linear_cache)
# print("dA_prev = " + str(dA_prev))
# print("dW = " + str(dW))
# print("db = " + str(db))
# GRADED FUNCTION: linear_activation_backward
def linear_activation_backward(dA, cache, activation):
"""
Implement the backward propagation for the LINEAR->ACTIVATION layer.
Arguments:
dA -- post-activation gradient for current layer l
cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
# # 测试linear_activation_backward
# print("==============测试linear_activation_backward==============")
# AL, linear_activation_cache = testCases.linear_activation_backward_test_case()
#
# dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation="sigmoid")
# print("sigmoid:")
# print("dA_prev = " + str(dA_prev))
# print("dW = " + str(dW))
# print("db = " + str(db) + "\n")
#
# dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation="relu")
# print("relu:")
# print("dA_prev = " + str(dA_prev))
# print("dW = " + str(dW))
# print("db = " + str(db))
# GRADED FUNCTION: L_model_backward
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {
}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# Lth layer (SIGMOID -> LINEAR) gradients.
# Inputs: "AL, Y, caches".
# Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = \
linear_activation_backward(dAL, current_cache, activation="sigmoid")
for l in reversed(range(L - 1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 2)], caches".
# Outputs: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)],
current_cache,
activation="relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
# # 测试L_model_backward
# print("==============测试L_model_backward==============")
# AL, Y_assess, caches = testCases.L_model_backward_test_case()
# grads = L_model_backward(AL, Y_assess, caches)
# print("dW1 = " + str(grads["dW1"]))
# print("db1 = " + str(grads["db1"]))
# print("dA1 = " + str(grads["dA1"]))
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of L_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
# # 测试update_parameters
# print("==============测试update_parameters==============")
# parameters, grads = testCases.update_parameters_test_case()
# parameters = update_parameters(parameters, grads, 0.1)
#
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))