【深度学习】数学基础

深度学习的主要应用

常用于非结构性数据：文字、音频、图像

图像处理领域主要应用

• 图像分类(物体识别)：整幅图像的分类或识别
• 物体检测：检测图像中物体的位置进而识别物体
• 图像分割：对图像中的特定物体按边缘进行分割
• 图像回归：预测图像中物体组成部分的坐标

语音识别领域主要应用

• 语音识别：将语音识别为文字
• 声纹识别：识别是哪个人的声音
• 语音合成：根据文字合成特定人的语音

自然语言处理领域主要应用

• 语言模型：根据之前词预测下一个单词。
• 情感分析：分析文本体现的情感(正负向、正负中或多态度类型)。
• 神经机器翻译：基于统计语言模型的多语种互译。
• 神经自动摘要：根据文本自动生成摘要。
• 机器阅读理解：通过阅读文本回答问题、完成选择题或完型填空。
• 自然语言推理：根据一句话(前提)推理出另一句话(结论)。

综合应用

• 图像描述：根据图像给出图像的描述句子
• 可视问答：根据图像或视频回答问题
• 图像生成：根据文本描述生成图像
• 视频生成：根据故事自动生成视频

数学基础

矩阵

矩阵的广义逆矩阵

• 如果矩阵不为方阵或者是奇异矩阵，不存在逆矩阵，但是可以计算其广义逆矩阵或者伪逆矩阵；
• 对于矩阵$A$，如果存在矩阵 $B$ 使得 $ABA=A$，则称 $B$为$ A$的广义逆矩阵。

矩阵分解

机器学习中常见的矩阵分解有特征分解和奇异值分解。

先提一下矩阵的特征值和特征向量的定义

• 若矩阵 $A$为方阵，则存在非零向量 $x$ 和常数 $\lambda$满足$Ax=\lambda x$，则称 $\lambda$为矩阵 $A$ 的一个特征值，$x$ 为矩阵 $A$关于 $\lambda$的特征向量。
• $A_{n\times n}$的矩阵具有 $n$个特征值，${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$ 其对应的n个特征向量为 ${\mathbf{u}}_1，{\mathbf{u}}_2，\cdots ，{\mathbf{u}}_n$
• 矩阵的迹(trace)和行列式(determinant)的值分别为

$$\mathrm{tr}(\mathrm{A})=\sum _{i=1}^n{\lambda }_i|\mathrm{A}|=\prod _{i=1}^n{\lambda }_i$$

矩阵特征分解：$A_{n\times n}$的矩阵具有 $n$个不同的特征值，那么矩阵A可以分解为 $A=U\Sigma U^T$.

其中 $\Sigma =\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]\mathrm{U}=\left[{\mathbf{u}}_1,{\mathbf{u}}_2,\cdots ,{\mathbf{u}}_n\right]{\Vert {\mathbf{u}}_i\Vert }_2=1$

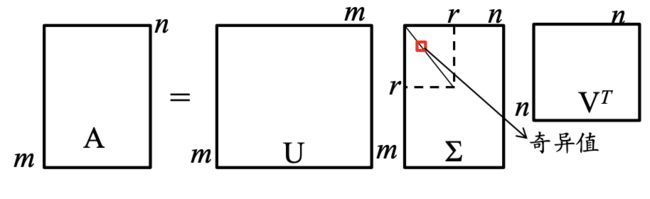
奇异值分解：对于任意矩阵$ A_{m \times n}$，存在正交矩阵 $U_{m\times m}$和 $V_{n\times n}$，使其满足 $A=U\Sigma V^T{U}^{T}U=V^{T}V=I$，则称上式为矩阵 AA 的特征分解。

概率统计

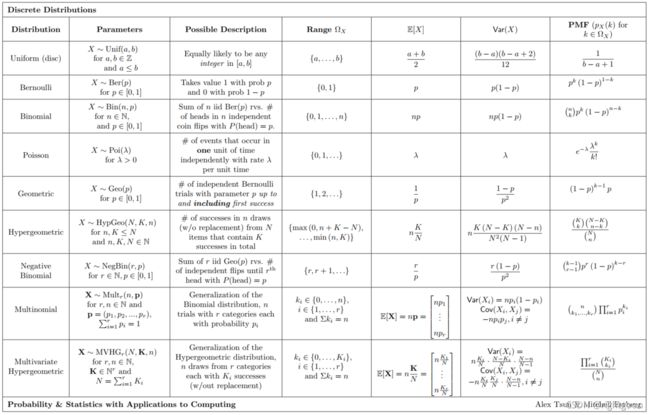
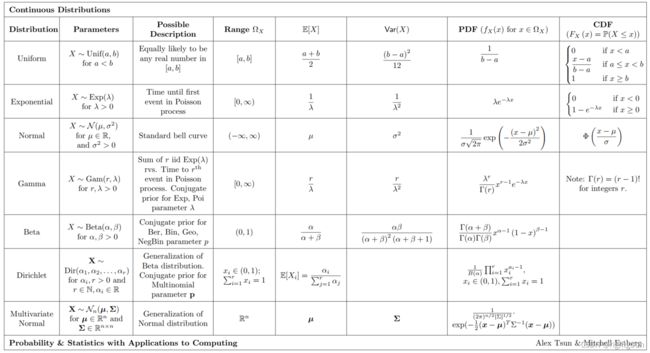
一些常见分布

先验概率(Prior probability)：根据以往经验和分析得到的概率，在事件发生前已知，它往往作为“由因求果”问题中的“因”出现。

后验概率(Posterior probability)：指得到“结果”的信息后重新修正的概率，是“执果寻因”问题中 的“因”，后验概率是基于新的信息，修正后来的先验概率所获得 的更接近实际情况的概率估计。

举例说明：一口袋里有3只红球、2只白球，采用不放回方式摸取，求: (1) 第一次摸到红球(记作A)的概率; (2) 第二次摸到红球(记作B)的概率; (3) 已知第二次摸到了红球，求第一次摸到的是红球的概率?

解：(1) $P(A=1)=3/5$， 这就是先验概率; (2)$P(B=1)=P(A=1)P(B=1|A=1)+P(A=0)P(B=1|A=0)=\frac{3}{5}\frac{2}{4}+\frac{2}{5}\frac{3}{4}=\frac{3}{5}$ (3) $P(A=1|B=1)=\frac{P(A=1)P(B=1|A=1)}{P(B=1)}=\frac{1}{2}$， 这就是后验概率。

信息论

熵(Entropy)

信息熵，可以看作是样本集合纯度一种指标，也可以认为是样本集合包含的平均信息量。

假定当前样本集合X中第i类样本 $x_i$所占的比例为$P(x_i)(i=1,2,...,n)$，则X的信息熵定义为：

$$H(X)=-\sum _{i=1}^{n}P(x_i){\log }_{2}P(x_i)$$

H(X)的值越小，则X的纯度越高，蕴含的不确定性越少

联合熵

两个随机变量X和Y的联合分布可以形成联合熵，度量二维随机变量XY的不确定性：

$$H(X,Y)=-\sum _{i=1}^n\sum _{j=1}^{n}P(x_i,y_j){\log }_{2}P(x_i,y_j)$$

条件熵

在随机变量X发生的前提下，随机变量Y发生带来的熵，定义为Y的条件熵，用H(Y|X)表示，定义为：

$$H(Y|X)=\sum _{i=1}^{n}P(x_i)H(Y|X=x_i)=-\sum _{i=1}^{n}P(x_i)\sum _{j=1}^{n}P(y_j|x_i){\log }_{2}P(y_j|x_i)=-\sum _{i=1}^n\sum _{j=1}^{n}P(x_i,y_j){\log }_{2}P(y_j|x_i)$$

条件熵用来衡量在已知随机变量X的条件下，随机变量Y的不确定。 熵、联合熵和条件熵之间的关系：

$$H(Y|X)=H(X,Y)-H(X)$$.

互信息

$$I(X;Y)=H(X)+H(Y)-H(X,Y)$$

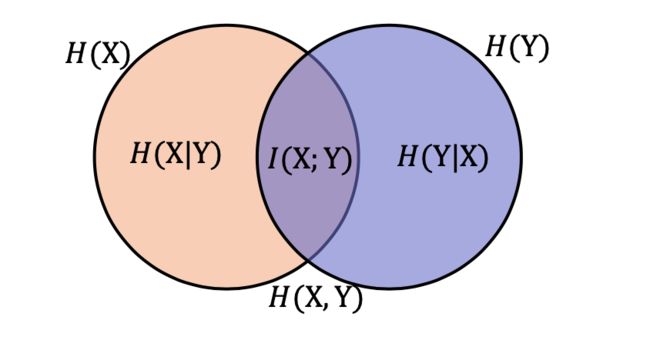
相对熵

相对熵又称KL散度，是描述两个概率分布P和Q差异的一种方法，记做D(P||Q)。在信息论中，D(P||Q)表示用概率分布Q来拟合真实分布P时，产生的信息表达的损耗，其中P表示信源的真实分布，Q表示P的近似分布。

• 离散形式：$D(P||Q)=\sum P(x)\log \frac{P(x)}{Q(x)}$
• 连续形式：$D(P||Q)=\int P(x)\log \frac{P(x)}{Q(x)}$

交叉熵

一般用来求目标与预测值之间的差距，深度学习中经常用到的一类损失函数度量，比如在对抗生成网络( GAN )中

$$D(P||Q)=\sum P(x)\log \frac{P(x)}{Q(x)}=\sum P(x)\log P(x)-\sum P(x)\log Q(x)=-H(P(x))-\sum P(x)\log Q(x)$$

交叉熵：$H(P,Q)=-\sum P(x)\log Q(x)$

参考：

• DataWhale 水很深的深度学习-数学基础
• CSE 312: Foundations of Computing II, Summer 2020 Handout