Datawhale开源教程学习——集成学习(task2机器学习基础模型)
目录
- Task02 机器学习基础模型
-
- 一、导论
-
- 使用sklearn构建完整的机器学习项目流程
- 二、作业
-
- Q1:详细阐述线性回归模型的最小二乘法表达。
- Q2:在线性回归模型中,极大似然估计与最小二乘估计有什么联系与区别。
- Q3:为什么多项式回归在在实际问题中的表现不是很好?
- Q4:决策树模型与线性模型之间的区别和联系?
- Q7:找一个数据集,使用线性回归模型拟合数据,要求不使用sklearn,只使用python和numpy。
Task02 机器学习基础模型
一、导论
机器学习的一个重要的目标就是利用数学模型来理解数据,发现数据中的规律,用作数据的分析和预测。
数据通常由一组向量组成,这组向量中的每个向量都是一个样本,我们用 x i x_i xi来表示一个样本,其中 i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N,共N个样本,每个样本 x i = ( x i 1 , x i 2 , . . . , x i p , y i ) x_i=(x_{i1},x_{i2},...,x_{ip},y_i) xi=(xi1,xi2,...,xip,yi)共p+1个维度,前p个维度的每个维度我们称为一个特征,最后一个维度 y i y_i yi我们称为因变量(响应变量)。
特征用来描述影响因变量的因素,如:我们要探寻身高是否会影响体重的关系的时候,身高就是一个特征,体重就是一个因变量。通常在一个数据表dataframe里面,一行表示一个样本 x i x_i xi,一列表示一个特征。
根据数据是否有因变量,机器学习的任务可分为:有监督学习和无监督学习。
-
有监督学习:给定某些特征去估计因变量,即因变量存在的时候,我们称这个机器学习任务为有监督学习。 如:我们使用房间面积,房屋所在地区,环境等级等因素去预测某个地区的房价。
-
无监督学习:给定某些特征但不给定因变量,建模的目的是学习数据本身的结构和关系。如:我们给定某电商用户的基本信息和消费记录,通过观察数据中的哪些类型的用户彼此间的行为和属性类似,形成一个客群。注意,我们本身并不知道哪个用户属于哪个客群,即没有给定因变量。
根据因变量是否连续,有监督学习又分为回归和分类。
使用sklearn构建完整的机器学习项目流程
一般来说,一个完整的机器学习项目分为以下步骤:
- 明确项目任务:回归/分类
- 收集数据集并选择合适的特征。
- 选择度量模型性能的指标。
- 选择具体的模型并进行训练以优化模型。
- 评估模型的性能并调参。
二、作业
Q1:详细阐述线性回归模型的最小二乘法表达。
A1: 最小二乘估计:
我们需要衡量真实值 y i y_i yi与线性回归模型的预测值 w T x i w^Tx_i wTxi(w和x都可看成列向量,w的转置与x相乘即为一个数值)之间的差距,在这里我们和使用二范数的平方和L(w)来描述这种差距,即:
L ( w ) = ∑ i = 1 N ∣ ∣ w T x i − y i ∣ ∣ 2 2 = ∑ i = 1 N ( w T x i − y i ) 2 = ( w T X T − Y T ) ( w T X T − Y T ) T = w T X T X w − 2 w T X T Y + Y Y T L(w) = \sum\limits_{i=1}^{N}||w^Tx_i-y_i||_2^2=\sum\limits_{i=1}^{N}(w^Tx_i-y_i)^2 = (w^TX^T-Y^T)(w^TX^T-Y^T)^T = w^TX^TXw - 2w^TX^TY+YY^T\\ L(w)=i=1∑N∣∣wTxi−yi∣∣22=i=1∑N(wTxi−yi)2=(wTXT−YT)(wTXT−YT)T=wTXTXw−2wTXTY+YYT
因此,我们需要找到使得L(w)最小时对应的参数w,即: w ^ = a r g m i n L ( w ) \\ \hat{w} = argmin\;L(w)\\ w^=argminL(w)
为了达到求解最小化L(w)问题,我们应用高等数学的知识,使用求导来解决这个问题: ∂ L ( w ) ∂ w = 2 X T X w − 2 X T Y = 0 \\ \frac{\partial L(w)}{\partial w} = 2X^TXw-2X^TY = 0 ∂w∂L(w)=2XTXw−2XTY=0
因此: w ^ = ( X T X ) − 1 X T Y \\ \hat{w} = (X^TX)^{-1}X^TY w^=(XTX)−1XTY
几何解释:
在线性代数中,我们知道两个向量a和b相互垂直可以得出: < a , b > = a . b = a T b = 0

可以理解为,图中的垂直虚线以向量表示,为Y-Xw(Xw代表底边黄色三角形区域中的任意一条向量),垂直虚线与底平面X相互垂直。故如上式所示。
Q2:在线性回归模型中,极大似然估计与最小二乘估计有什么联系与区别。
A2:
假设噪声 ϵ ∽ N ( 0 , σ 2 ) , y = f ( w ) + ϵ = w T x + ϵ \epsilon \backsim N(0,\sigma^2),y=f(w)+\epsilon=w^Tx+\epsilon ϵ∽N(0,σ2),y=f(w)+ϵ=wTx+ϵ,因此: y ∣ x i , w N ( w T x , σ 2 ) y|x_i,w ~ N(w^Tx,\sigma^2) y∣xi,w N(wTx,σ2)
我们使用极大似然估计MLE对参数w进行估计:
L ( w ) = l o g P ( Y ∣ X ; w ) = l o g ∏ i = 1 N P ( y i ∣ x i ; w ) = ∑ i = 1 N l o g P ( y i ∣ x i ; w ) = ∑ i = 1 N l o g ( 1 2 π σ e x p ( − ( y i − w T x i ) 2 2 σ 2 ) ) = ∑ i = 1 N [ l o g ( 1 2 π σ ) − 1 2 σ 2 ( y i − w T x i ) 2 ] a r g m a x w L ( w ) = a r g m i n w [ l ( w ) = ∑ i = 1 N ( y i − w T x i ) 2 ] L(w) = log\;P(Y|X;w) = log\;\prod_{i=1}^N P(y_i|x_i;w) = \sum\limits_{i=1}^{N} log\; P(y_i|x_i;w)\\ = \sum\limits_{i=1}^{N}log(\frac{1}{\sqrt{2\pi \sigma}}exp(-\frac{(y_i-w^Tx_i)^2}{2\sigma^2})) = \sum\limits_{i=1}^{N}[log(\frac{1}{\sqrt{2\pi}\sigma})-\frac{1}{2\sigma^2}(y_i-w^Tx_i)^2] \\ argmax_w L(w) = argmin_w[l(w) = \sum\limits_{i = 1}^{N}(y_i-w^Tx_i)^2]\\ L(w)=logP(Y∣X;w)=logi=1∏NP(yi∣xi;w)=i=1∑NlogP(yi∣xi;w)=i=1∑Nlog(2πσ1exp(−2σ2(yi−wTxi)2))=i=1∑N[log(2πσ1)−2σ21(yi−wTxi)2]argmaxwL(w)=argminw[l(w)=i=1∑N(yi−wTxi)2]
因此:线性回归的最小二乘估计等价于 噪声 ϵ ∽ N ( 0 , σ 2 ) \epsilon\backsim N(0,\sigma^2) ϵ∽N(0,σ2)的极大似然估计
解释:假设噪声属于正态分布,那么y也是正态分布,故使用极大似然估计对参数w进行估计。由于是极大似然估计,也就是对下面式子求最大
∑ i = 1 N [ l o g ( 1 2 π σ ) − 1 2 σ 2 ( y i − w T x i ) 2 ] \sum\limits_{i=1}^{N}[log(\frac{1}{\sqrt{2\pi}\sigma})-\frac{1}{2\sigma^2}(y_i-w^Tx_i)^2] \\ i=1∑N[log(2πσ1)−2σ21(yi−wTxi)2]
那么就转换为对下面这个式子求最小
1 2 σ 2 ( y i − w T x i ) 2 ] \frac{1}{2\sigma^2}(y_i-w^Tx_i)^2] \\ 2σ21(yi−wTxi)2]
所以就相当于前面的最小二乘估计,所以线性回归的最小二乘估计等价于存在噪声的极大似然估计。
Q3:为什么多项式回归在在实际问题中的表现不是很好?
A3:
在线性回归中,我们假设因变量与特征之间的关系是线性关系,这样的假设使得模型很简单,但是缺点也是显然的,那就是当数据存在非线性关系时,我们使用线性回归模型进行预测会导致预测性能极其低下,因为模型的形式本身是线性的,无法表达数据中的非线性关系。我们一个很自然的想法就是去推广线性回归模型,使得推广后的模型更能表达非线性的关系。
(a) 多项式回归:
为了体现因变量和特征的非线性关系,一个很自然而然的想法就是将标准的线性回归模型:
y i = w 0 + w 1 x i + ϵ i y_i = w_0 + w_1x_i + \epsilon_i yi=w0+w1xi+ϵi
换成一个多项式函数:
y i = w 0 + w 1 x i + w 2 x i 2 + . . . + w d x i d + ϵ y_i = w_0 + w_1x_i + w_2x_i^2 + ...+w_dx_i^d + \epsilon yi=w0+w1xi+w2xi2+...+wdxid+ϵ
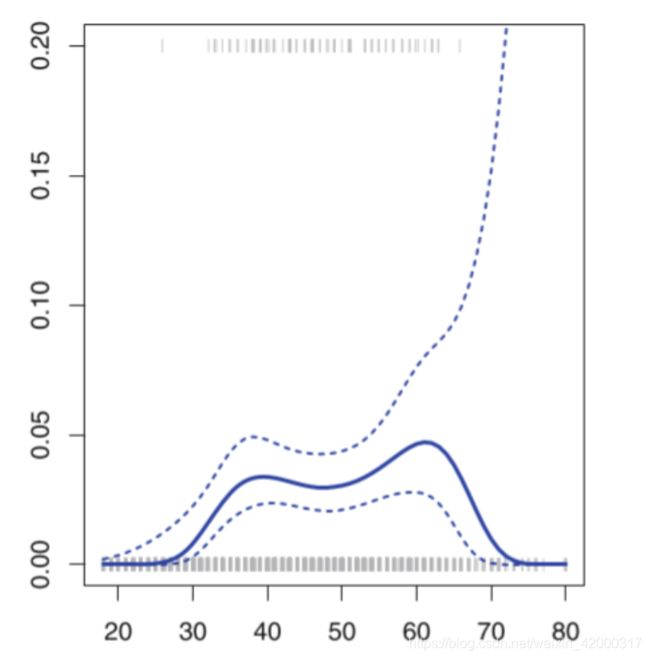
对于多项式的阶数d不能取过大,一般不大于3或者4,因为d越大,多项式曲线就会越光滑,在X的边界处有异常的波动。(图中的边界处的4阶多项式拟合曲线的置信区间(虚线表示置信区间)明显增大,预测效果的稳定性下降。)

这个图蓝色实线代表预测的曲线,虚线代表两侧置信区间。置信区间是越小越好,越大则越不确定。由于数据量大多集中在中间,所以在边侧的置信区间线不是很贴合。
下图是4阶多项式的预测图。如果阶数d很大,可以看出置信区间很大,故不准确。
Q4:决策树模型与线性模型之间的区别和联系?
A4:
回归树与线性模型的比较:
线性模型的模型形式与树模型的模型形式有着本质的区别,具体而言,线性回归对模型形式做了如下假定: f ( x ) = w 0 + ∑ j = 1 p w j x ( j ) f(x) = w_0 + \sum\limits_{j=1}^{p}w_jx^{(j)} f(x)=w0+j=1∑pwjx(j),而回归树则是 f ( x ) = ∑ m = 1 J c ^ m I ( x ∈ R m ) f(x) = \sum\limits_{m=1}^{J}\hat{c}_mI(x \in R_m) f(x)=m=1∑Jc^mI(x∈Rm)(是属于一块区域的加权平均)。那么模型更优要视具体情况而言,如果特征变量与因变量的关系能很好的用线性关系来表达,那么线性回归通常有着不错的预测效果,拟合效果则优于不能揭示线性结构的回归树。反之,如果特征变量与因变量的关系呈现高度复杂的非线性,那么树方法比传统方法更优。
树模型的优缺点:
- 树模型的解释性强,在解释性方面可能比线性回归还要方便。
- 树模型更接近人的决策方式。
- 树模型可以用图来表示,非专业人士也可以轻松解读。
- 树模型可以直接做定性的特征而不需要像线性回归一样哑元化(个人理解就是变成数字的形式,类似one-hot?)。
- 树模型能很好处理缺失值和异常值,对异常值不敏感,但是这个对线性模型来说却是致命的。(树模型可以把缺失值当成一个类别,而线性模型通常用均值来填补缺失值)(对距离有要求的算法都会对异常值敏感)
- 树模型的预测准确性一般无法达到其他回归模型的水平(树模型容易过拟合),但是改进的方法很多(如集成学习等)。
待补充:sklearn使用回归树的例子
Q7:找一个数据集,使用线性回归模型拟合数据,要求不使用sklearn,只使用python和numpy。
待补充
