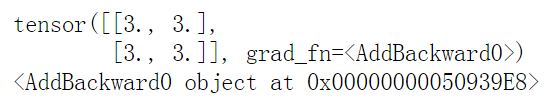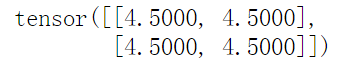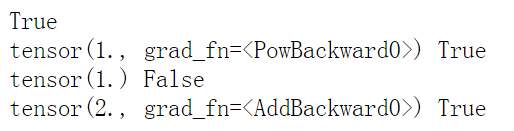《动手学深度学习》(Pytorch版) 学习笔记—— 2.3 自动求梯度
文章目录
- 前言
- 1 概念
- 2 Tensor
- 3 梯度
-
- 3.1 一些实际例子
-
- 3.1.1
- 3.1.2 中断梯度追踪的例子
- 3.1.3
前言
Python初学者一枚,文章仅为个人学习记录,便于以后查看使用。
深度学习中,我们经常需要对函数求梯度(gradient)。
PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图,并执行反向传播。
1 概念
Tensor是这个包的核心类。
如果将其属性.requires_grad设置为True,它将开始追踪(track)在其上的所有操作(这样就可以利用链式法则进行梯度传播了)。
完成计算后,可以调用.backward()来完成所有梯度计算。
此Tensor的梯度将累积到.grad属性中。
注意:在y.backward()时,如果y是标量,不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor。详见 2 节。
如果不想被继续追踪,可以调用.detach()将其从追踪记录中分离出来,这样就可以防止将来的计算被追踪,这样梯度就传不过去了。
还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来。
这种方法在评估模型的时候很常用,因为在评估模型时,我们并不需要计算可训练参数(requires_grad=True)的梯度。
Function是另外一个很重要的类。
Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图(DAG)。
每个Tensor都有一个.grad_fn属性,该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的,若是,则grad_fn返回一个与这些运算相关的对象,否则是None。
2 Tensor
创建一个Tensor并设置requires_grad=True:
x = torch.ones(2, 2, requires_grad=True)
print(x)
print(x.grad_fn)
做一下运算操作:
y = x + 2
print(y)
print(y.grad_fn)
注意:x是直接创建的,所以它没有grad_fn, 而y是通过一个加法操作创建的,所以它有一个为< AddBackward >的grad_fn。
像x这种直接创建的称为叶子节点,叶子节点对应的grad_fn是None。
print(x.is_leaf, y.is_leaf)
再来点复杂度运算操作:
z = y * y * 3
out = z.mean()
print(z, out)
通过.requires_grad_()来用in-place的方式改变requires_grad属性:
a = torch.randn(2, 2) # 缺失情况下默认 requires_grad = False
a = ((a * 3)) / (a - 1)
print(a.requires_grad) # False
a.requires_grad_(True)
print(a.requires_grad) # True
b = (a * a).sum()
print(b.grad_fn)
3 梯度
因为out是一个标量,所以调用backward()时不需要指定求导变量:
out.backward() # 等价于 out.backward(torch.tensor(1.))
out关于x的梯度 d(out)/dx :
print(x.grad)
所以上面的输出是正确的。
那么向量y关于向量x的梯度就是一个雅可比矩阵(Jacobian matrix):
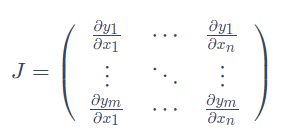
而torch.autograd这个包就是用来计算一些雅克比矩阵的乘积的。
例如,如果 vv 是下图标量函数
![]()
的梯度:

注意:grad在反向传播过程中是累加的(accumulated),这意味着每一次运行反向传播,梯度都会累加之前的梯度,所以一般在反向传播之前需把梯度清零。
# 再来反向传播一次,注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)
out3 = x.sum()
x.grad.data.zero_()
out3.backward()
print(x.grad)
▲▲▲为什么在y.backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor?
简单来说,是为了避免向量(甚至更高维张量)对张量求导,而转换成标量对张量求导。

所以必要时我们要把张量通过将所有张量的元素加权求和的方式转换为标量。
![]()
3.1 一些实际例子
3.1.1
x = torch.tensor([1.0, 2.0, 3.0, 4.0], requires_grad=True)
y = 2 * x
z = y.view(2, 2)
print(z)
现在 z 不是一个标量,所以在调用backward时需要传入一个和z同形的权重向量进行加权求和得到一个标量。
v = torch.tensor([[1.0, 0.1], [0.01, 0.001]], dtype=torch.float)
z.backward(v)
print(x.grad)
注意:x.grad是和x同形的张量。
3.1.2 中断梯度追踪的例子
x = torch.tensor(1.0, requires_grad=True)
y1 = x ** 2
with torch.no_grad():
y2 = x ** 3
y3 = y1 + y2
print(x.requires_grad)
print(y1, y1.requires_grad) # True
print(y2, y2.requires_grad) # False
print(y3, y3.requires_grad) # True
y2没有grad_fn且y2.requires_grad=False,y3有grad_fn。
将y3对x求梯度:
y3.backward()
print(x.grad)
输出:
![]()
▲▲▲为什么是2不是5?
由于Y2的定义是被torch.no_grad():包裹的,所以与y2有关的梯度是不会回传的,只有与 y1有关的梯度才会回传。

上面提到,y2.requires_grad=False,所以不能调用 y2.backward(),会报错:
![]()
3.1.3
如果我们想要修改tensor的数值,但是又不希望被autograd记录(即不会影响反向传播),那么可以对tensor.data进行操作。
x = torch.ones(1,requires_grad=True)
print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经独立于计算图之外
y = 2 * x
x.data *= 100 # 只改变了值,不会记录在计算图,所以不会影响梯度传播
y.backward()
print(x) # 更改data的值也会影响tensor的值
print(x.grad)