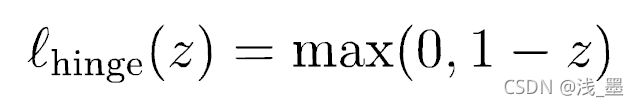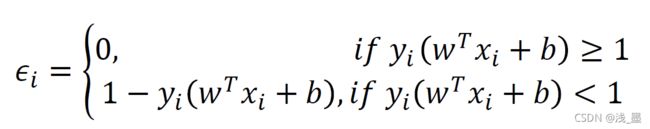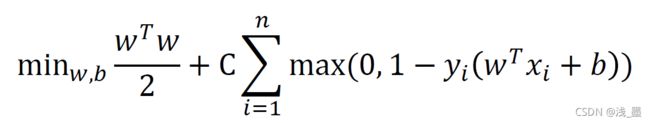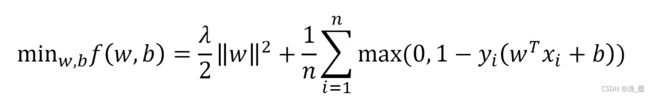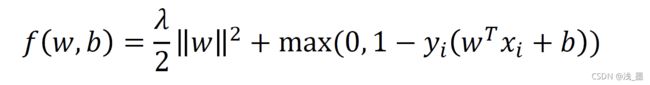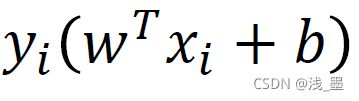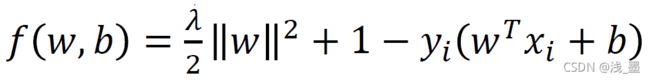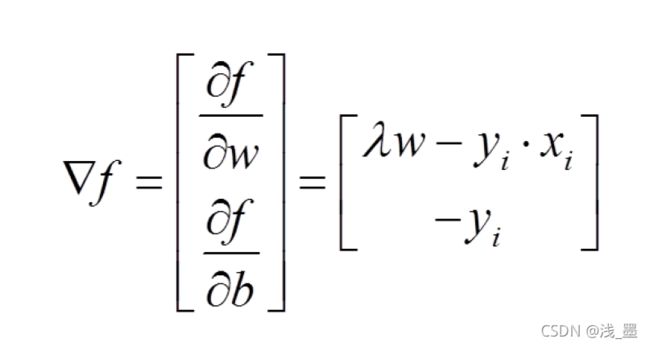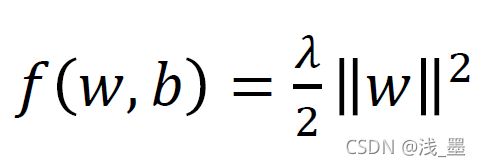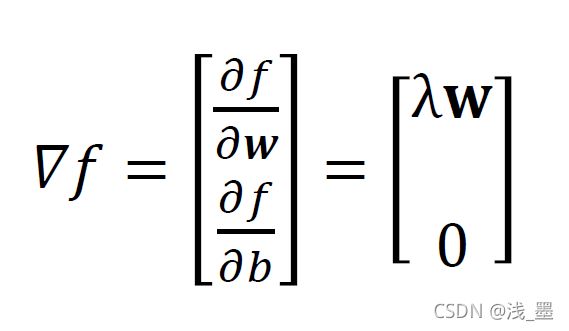Python使用佩加索斯（Pegasos）算法实现软间隔SVM

一.软间隔SVM目标函数推导

SVM假定存在一个超平面能够将两类样本完全分隔开来，但在实际情况中，数据是不能被一个平面完全分隔的，因此，为了使得问题可解，我们需要在原SVM的优化问题上加入松弛变量ε，ε是一个大于等于0的数，引入松弛变量后，原优化问题转化为：

                               

其中，C是正则化常数，其取值越大，则表示对误分类的惩罚越大，即要求越严格。不难看出，当ε=0时，该问题将会成为标准的SVM优化问题.

引入松弛变量后，其约束条件变为：

                                  

由于标签y的取值为-1或1，则其约束条件可以简化为：

                            

那么，我们应该如何求得该目标函数的最优解呢？

首先，需要构建损失函数，我们通过惩罚错误分类的数目来实现，在这里，采用hinge损失函数：

                                   

 则松弛变量ε可以用该损失函数来表示：

                            

其含义为，当分类正确时，即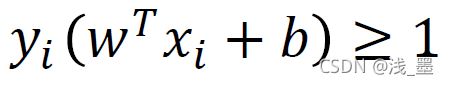时，松弛变量为0，即不进行惩罚，当分类失败时，对其进行惩罚。

则目标函数可以简化为：

                          

 令C = 1/(nλ), 给公式整体xλ得到目标函数：

                          

 对于一个随机选择的样本点，目标函数为：

                         

二. 佩加索斯算法

对于该目标函数，我们可以使用梯度下降法来求解该目标函数。

当<1时，，则：

                              

当>1时，，则：

                               

此时，我们得到了目标函数对两个参数的梯度，则我们可以通过梯度下降的方式来优化参数：

                        

     其中η_t为学习率，η_t = 1/(λt),t为训练的轮次，其作用是控制参数优化的步长，当训练轮数越多时，参数优化步长越小。

得到参数的更新公式后，我们采用随机梯度下降的方式训练模型，训练步骤如下：

                    

 

 这便是佩加索斯算法，使用该算法，可以在O(N)的时间复杂度内训练模型，十分高效。

三. 佩加索斯算法代码实现

def svm(data,label,lamda,n):
    row,col = np.shape(data)
    w = np.zeros(col)
    b = 0.0
    for i in range(1,n+1):
        r = random.randint(0,row-1)
        eta = 1.0/(lamda*i)
        predict = forward(w,b,data[r])
        if label[r] * predict < 1:
            w = w - w/i + eta * label[r] * data[r]
            b = b + eta * label[r]
        else:
            w = w - w/i
    return w,b

 预测时，只需要计算WX+b即可：

def forward(w,b,x):
    return w*x.T + b

 在这里，贴上一段使用svm分类垃圾邮件的代码，邮件数据集中训练样本已转换为词向量，原始标签为（0，1），因此，在使用SVM分类时需要先将标签转为（-1，1）。

'''
返回测试数据,test_data['Xtest']为数据,test_data['ytest']为标签
'''
def load_test_data():
    test_data = loadmat('./data/spamTest.mat')
    test_label = []
    for item in test_data['ytest']:
        if item[0] == 0:
            test_label.append([-1])
        else:
            test_label.append([1])

    return np.mat(test_data['Xtest']),np.mat(test_label)

 完整代码如下：

import random
import numpy as np
from scipy.io import loadmat

'''
返回训练数据,train_data['X']为数据,train_data['y']为标签
'''
def load_train_data():
    train_data = loadmat('./data/spamTrain.mat')
    label = []
    for item in train_data['y']:
        if item[0] == 0:
            label.append([-1])
        else:
            label.append([1])
    return np.mat(train_data['X']),np.mat(label)

'''
返回测试数据,test_data['Xtest']为数据,test_data['ytest']为标签
'''
def load_test_data():
    test_data = loadmat('./data/spamTest.mat')
    test_label = []
    for item in test_data['ytest']:
        if item[0] == 0:
            test_label.append([-1])
        else:
            test_label.append([1])

    return np.mat(test_data['Xtest']),np.mat(test_label)

def forward(w,b,x):
    return w*x.T + b


def svm(data,label,lamda,n):
    row,col = np.shape(data)
    w = np.zeros(col)
    b = 0.0
    for i in range(1,n+1):
        r = random.randint(0,row-1)
        eta = 1.0/(lamda*i)
        predict = forward(w,b,data[r])
        if label[r] * predict < 1:
            w = w - w/i + eta * label[r] * data[r]
            b = b + eta * label[r]
        else:
            w = w - w/i
    return w,b

def test(w,b):
    test_data,test_label = load_test_data()
    pre_list = []
    for item in test_data:
        y_pre = forward(w,b,item)
        if y_pre[0][0]>0:
            pre_list.append(1)
        else:
            pre_list.append(-1)
    count = 0
    for i in range(len(pre_list)):
        if(pre_list[i] == test_label[i][0]):
            count += 1
    print("The accuracy is:",count/len(pre_list))

def train():
    train_data, train_label = load_train_data()
    w,b = svm(train_data,train_label,0.1,2000)
    return w,b

if __name__ == '__main__':
    for i in range(10):
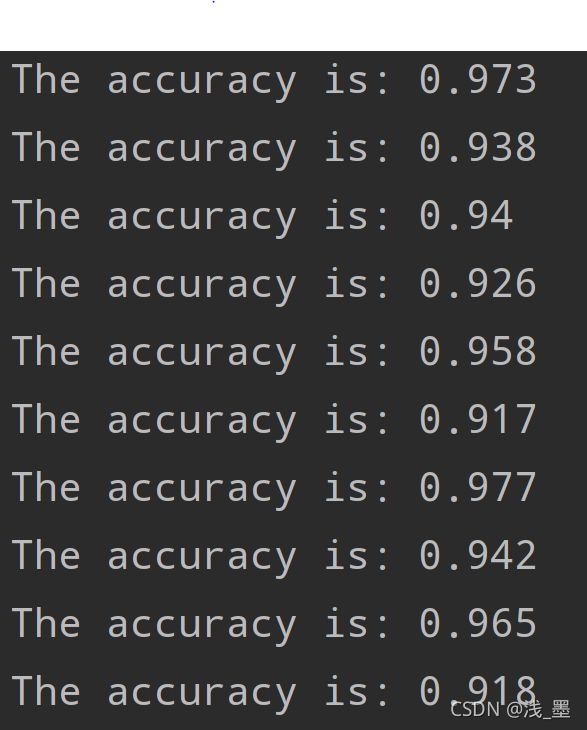
        w,b = train()
        test(w,b)

 在λ = 0.1时，分类准确率最高可以达到97.7%。

四. 数据集

数据集链接如下：

链接：https://pan.baidu.com/s/1LkAZaw-gPc4FXRmD8jpGJQ 
提取码：8h82