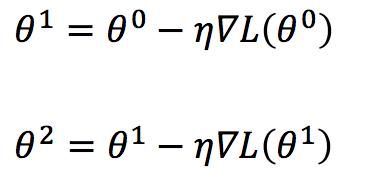小白机器学习基础算法学习必经之路
https://www.toutiao.com/a6657427848900379150/
2019-02-14 15:21:13
未来,人工智能是生产力,是变革社会的主要技术力量之一。 掌握人工智能技术,需要从基础的机器学习算法开始学习,逐渐建立机器学习知识体系。
本场篇文章 :
- 带大家克服心理上对于机器学些的敬畏,绕开弯路(本人入过很多坑),进入机器学习领域。
- 从基本概念和机器学习的应用领域入手,帮助大家建立机器学习的概念模型。
- 用最基本的线性回归和逻辑回归算法,让大家掌握机器学习神秘的“三板斧”方法论。
- 通过自身多年的学习经验,举一反三,引导大家科学建立机器学习和深度学习的学习路线。
一. 引言
首先,我们看一下在Quora(美国知乎)上的三个问题和专家回答。1. 我能在没有计科硕士、博士文凭的情况下找到一份关于机器学习的工作吗? “你当然可以,但是想进入这个领域则无比艰难。” --Drac Smith
2. 我是一名软件工程师,我自学了机器学习,我如何在没有相关经验的情况下找到一份关于机器学习的工作?
“我正在为我的团队招聘机器学习专家,但你的MOOC并不会给你带来工作机会。事实上,大多数机器学习方向的硕士也并不会得到工作机会,因为他们(与大多数上过MOOC的人一样)并没有深入地去理解。他们都没法帮助我的团队解决问题。”-- Ross C. Taylor
3. 找一份机器学习相关的工作需要掌握怎样的技能?
“首先,你得有正儿八经的计科或数学专业背景。ML是一个比较先进的课题,大多数的教材都会直接默认你有以上背景。其次,机器学习是一个集成了许多子专业的奇技淫巧的课题,你甚至会想看看MS的机器学习课程,去看看他们的授课、课程和教材。”“统计,假设,分布式计算,然后继续统计。” --Hydrangea
通过以上三个问题好专业人士的回答,很多机器学习小白可能会望而却步。
其实,我通过自身的学习经验,长期坚持和积累,发现机器学习的内在规律,分享出来,让大家克服心理恐惧,高效的投入的机器学习课程中。
再举一些机器学习大牛的例子:
- Kaggle Grandmaster Evgeny Patekha:四十岁才开始数据科学生涯
- Kaggle Grandmaster Alexander Larko:五十五岁才开始参加Kaggle竞赛
说明任何时候学习都不嫌晚!但是一定要有正确的方法和坚毅的态度。
好吧,那么我们就进入机器学习的世界。
二、机器学习的概念
究竟什么是机器学习?
这个问题回答如果在教科书,可能会很复杂。但是能够把复杂的问题简单化,是一件见不太容易的事情(需要足够的功力)。但是我尽量为大家这样做。
机器学习就是需找一种函数f(x),这种函数能够做预测、分类、生成等工作。
那么,找到这个函数f(x)是机器学习者的核心任务。下面的讲到的“方法论”核心就是如何去f(x)。
三、机器学习的“三板斧”方法论
机器学习的过程和把大象放冰箱一样,一共分三步:
step_1: 定义一个函数集合(define a function set)
step_2: 判断函数的好坏(goodness of a function)
step_3: 选择最好的函数(pick the best one)**
首先,进人用“三板斧”解决机器学习中最基本的回归(预测)、分类问题之前,我们进行一下准备活动。
准备活动1:学习梯度下降
三板斧中的核心步骤- 步骤3: 选择最好的函数。
步骤3中,如何选择好的神经网络(f(x))的呢?
$L( heta)$ 代表判断函数的好坏(一般为与真实值的差距,差距越小越好)
我们的目标是让$L( heta)$ 最小化:
这里我们就引入梯度下降(高等数学中的基本概念):
梯度下降机器学习、深度学习中最重要的概念之一:
梯度下降是目前,最有效的方法之一。
方法:我们举两个参数的例子$ heta1$,$ heta2$, 损失函数是L。那么它的梯度是:
那我为了求得最小值,我们有:
参数不断被梯度乘以学习率η 迭代
那么上述公示公为什么是减号,不是加号呢? 我们定义$ heta$改变的方向是movement的方向, 而gradient的方向是等高线的法线方向
准备活动2:了解Keras
Kearas 是机器学习、深度学习小白代码入门的最佳工具之一。
如果想提升、练习代码能力,还是建议算法徒手python实现。 复杂的深度神经网络项目还是推荐TensorFlow或者Pytorch
简介:
- Keras是一个高级神经网络API,Keras由纯Python编写而成并基Tensorflow、Theano以及CNTK后端。
- Keras 为支持快速实验而生,能够把你的idea迅速转换为结果,如果你有如下需求,请选择Keras:
- 简易和快速的原型设计(keras具有高度模块化,极简,和可扩充特性)支持CNN和RNN,或二者的结合无缝CPU和GPU切换。
为了更加生动的让小白同学克服机器学习、深度学习编程的恐惧心理,我再这里给出一幅图:
机器学习,尤其是深度学习编程strong text其实是:搭积木!
介绍完本次代码演示的工具后,我们就用实际经典的机器学习的代码,手握“三板斧”,带大家进入机器学习的世界。
机器学习最重要的问题,主要是在回归(预测)、和分类,我们的例子包含这两大类。
1. 线性回归
- 问题 给下面一组数据,用一条线来对数据进行拟合,并可以预测新输入 x 的输出值。
- 创建数据(模拟数据)
- # create some data
- X = np.linspace(-1, 1, 200)
- # randomize the data
- np.random.shuffle(X)
- Y = 0.5 * X + 2 + np.random.normal(0, 0.05, (200, ))
- # plot data
- plt.scatter(X, Y)
- plt.show()
- # train 前 160 data points
- X_train, Y_train = X[:160], Y[:160]
- # test 后 40 data points
- X_test, Y_test = X[160:], Y[160:]
可视化创建的数据集如下:
下面就是三板斧了:
(1) 线性回归- 徒手代码版(推荐)
我们定义函数集合为:$y= heta_{1}*x+ heta_{0} $, m=160(训练数据的量)
# 第一板斧:定义一个函数集合
X = np.c_[np.ones(m), X]
theta = np.zeros(2)
# Some gradient descent settings
iterations = 1500
alpha = 0.01
# 第二板斧:判断函数的好坏(本例中用的是MSE 均方误差)
cost = np.sum((np.dot(X, theta) - y) ** 2) / (2 * m)
# 第三板斧:选择最好的函数(theta 让Loss最小)
theta = gradient_descent(X_train,Y_train, theta, alpha, iterations, cost)
# 结果
predict = np.dot(X_test, theta)
注: gradient_descent 函数的实现我们暂时忽略,但是原理大家已经掌握。 我们的预测结果如下:
(2) 线性回归- Kears 神经网络版
三板斧1:定义一个函数集合(建立神经网络模型) 我们定义函数集合为:$y= heta_{1}*x+ heta_{0} $
我们用 神经网络来拟合这样函数。
Sequential 建立 model, 再用 model.add 添加神经层,添加的是 Dense 全连接神经层。
参数有两个,一个是输入数据和输出数据的维度,本代码的例子中 x 和 y 是一维的。
如果需要添加下一个神经层的时候,不用再定义输入的纬度,因为它默认就把前一层的输出作为当前层的输入。在这个例子里,只需要一层就够了。(即使是一层神经网络可以拟合任何函数)
model = Sequential()
model.add(Dense(output_dim=1, input_dim=1))
三板斧2:判断函数的好坏 误差函数是判断函数好坏的主要方式,本例中用的是MSE 均方误差; 优化器用的是 sgd 随机梯度下降法(一种能让MSE找到最小值的通用方法)
# choose loss function and optimizing method model.compile(loss=‘mse’, optimizer=‘sgd’)
三板斧3:选择最好的函数(训练模型)
训练的时候用 model.train_on_batch 一批一批的训练 X_train, Y_train。默认的返回值是 cost,每100步输出一下结果。
# training
print('Training -----------')
for step in range(301):
cost = model.train_on_batch(X_train, Y_train)
if step % 100 == 0:
print('train cost: ', cost)
"""
Training -----------
train cost: 4.111329555511475
train cost: 0.08777070790529251
train cost: 0.007415373809635639
train cost: 0.003544030711054802
"""
三板斧过后,我们检验一下我们模型:
用到的函数是 model.evaluate,输入测试集的x和y, 输出 cost,weights 和 biases。其中 weights(theta0) 和 biases(theta1) 是取在模型的第一层 model.layers[0] 学习到的参数。从学习到的结果你可以看到, weights 比较接近0.5,bias 接近 2。
# test
print(' Testing ------------')
cost = model.evaluate(X_test, Y_test, batch_size=40)
print('test cost:', cost)
theta1, theta0 = model.layers[0].get_weights()
print('Weights=', theta1, ' biases=', theta0 )
"""
Testing ------------
40/40 [==============================] - 0s
test cost: 0.004269329831
Weights= [[ 0.54246825]]
biases= [ 2.00056005]
"""
可视化结果 :
# plotting the prediction
Y_pred = model.predict(X_test)
plt.scatter(X_test, Y_test)
plt.plot(X_test, Y_pred)
plt.show()
我们的回归问题,通过找到函数的参数theta1 =0.5,theta0 =2.0,已经完成:
2. 分类
分类问题中,我们使用深度学习的“Hello World”,手写数字识别作为例子。 手写数字识别。用最简单的DNN神经网络实现。
Keras 自身就有 MNIST 这个数据包,再分成训练集和测试集。x 是一张张图片,y 是每张图片对应的标签,即它是哪个数字。
输入的 x 变成 60,000*784 的数据,然后除以 255 进行标准化,因为每个像素都是在 0 到 255 之间的,标准化之后就变成了 0 到 1 之间。
对于 y,要用到 Keras 改造的 numpy 的一个函数 np_utils.to_categorical,把 y 变成了 one-hot 的形式,即之前 y 是一个数值, 在 0-9 之间,现在是一个大小为 10 的向量,它属于哪个数字,就在哪个位置为 1,其他位置都是 0。
from keras.datasets import mnist
# download the mnist to the path '~/.keras/datasets/' if it is the first time to be called
# X shape (60,000 28x28), y shape (10,000, )
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# data pre-processing
X_train = X_train.reshape(X_train.shape[0], -1) / 255. # normalize
X_test = X_test.reshape(X_test.shape[0], -1) / 255. # normalize
y_train = np_utils.to_categorical(y_train, num_classes=10)
y_test = np_utils.to_categorical(y_test, num_classes=10)
print(X_train[1].shape)
"""
(784,)
"""
print(y_train[:3])
"""
[[ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]
"""
我们的三板斧又可以登场了:
三板斧1:定义一个函数集合(建立神经网络模型):
在回归网络中用到的是 model.add 一层一层添加神经层,以下图片分类的方法是直接在模型的里面加多个神经层。好比一个水管,一段一段的,数据是从上面一段掉到下面一段,再掉到下面一段。
第一段就是加入 Dense 神经层。32 是输出的维度,784 是输入的维度。 第一层传出的数据有 32 个 feature,传给激励单元,激励函数用到的是 relu 函数。 经过激励函数之后,就变成了非线性的数据。 然后再把这个数据传给下一个神经层,这个 Dense 我们定义它有 10 个输出的 feature。同样的,此处不需要再定义输入的维度,因为它接收的是上一层的输出。 接下来再输入给下面的 softmax 函数,用来分类。
model = Sequential([
Dense(32, input_dim=784),
Activation('relu'),
Dense(10),
Activation('softmax'),
])
三板斧2:判断函数的好坏:
损失函数,分类和回归问题的不一样,用的是交叉熵(信息学的概念,其实就是两个组概率分布相似程度)。
用 RMSprop 作为优化器(暂时可以认为是一种让Loss稳定减少的工具),它的参数包括学习率等,可以通过修改这些参数来看一下模型的效果。
rmsprop = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
model.compile(optimizer=rmsprop, loss=‘categorical_crossentropy’, metrics=[‘accuracy’])
三板斧3:选择最好的函数(训练模型)
这里用到的是 fit 函数,把训练集的 x 和 y 传入之后,nb_epoch 表示把整个数据训练多少次,batch_size 每批处理32个。
model.fit(X_train, y_train, epoch=20, batch_size=100) “”" Training ------------ Epoch 1/2 60000/60000 [==============================] - 2s - loss: 0.3506 - acc: 0.9025
Epoch 2/2 60000/60000 [==============================] - 2s - loss: 0.1995 - acc: 0.9421
“”" 三板斧过后,我们检验一下我们模型:
print(' Testing ------------')
# Evaluate the model with the metrics we defined earlier
loss, accuracy = model.evaluate(X_test, y_test)
print('test loss: ', loss)
print('test accuracy: ', accuracy)
"""
Testing ------------
9760/10000 [============================>.] - ETA: 0s
test loss: 0.1724540345
test accuracy: 0.9489
"""
我们的回归问题已经完成:分类准确率已经达到94.89%。
四、机器学习的推荐学习路线
1.学习准备:
(1) 数学篇 高等数学: 微分部分即可(掌握微分原理) 线性代数: 掌握矩阵的基本运算、矩阵微分、Jacobian矩阵和Hessian矩阵 (2) 英语篇: 具有大学英语4级水平 (3) 编程篇: 具有使用Python解决基础数据结构问题的能力
2.学习路线(1年):
推荐直接学习国外一流大学的高水平视频课程,同步写课程作业,学习路线共分4步,
(1) 机器学习基础算法(3个月)
- 国外课程推荐:吴恩达机器学习(斯坦福大学CS229)
- 国内教材推荐: 《机器学习》 周志华 《统计学习方法》李航
- 《机器学习课》邹博
(2) 深度学习(6个月)
- 计算机视觉(斯坦福大学CS231N)(3个月)
- 自然语言处理(斯坦福大学CS224N)(3个月)
(3) 机器学习编程框架(1个月)
- Tensorflow(斯坦福大学CS20I)
- PyTorch
(4) 强化学习(2个月)
- UCL-Course(伦敦大学学院 ) (AlphaGo之父 David Silver)
3. 学习宝典:
(1) 创建博客
- CSDN
- 知乎
(2) 打AI比赛
- 天池
- Kaggle
(3) 创建Github
- 课程作业
- 比赛代码
- 学习项目
(4) 读高水平英文论文
深度学习经典论文
4. 编程建议:
编写代码是机器学习、深度学习有力的武器,但是也是需要循序渐进,不能一开始就使用“重武器”(框架),这样对基本的概念和掌握会很不牢靠,而且容易沾沾自喜,感觉自己都掌握了,其实不然。
建议路线:
- python 徒手算法实现
- 使用sklearn等基础的机器学习库
- 学习Tensorflow或者Pytorch
- 学习Keras
五、机器学习的学习资料
1.数学知识
1.线性代数
2.概率论
3.凸函数优化
4.随机梯度下降算法
5. 机器学习中的数学基本知识
6.统计学习方法
2.编程知识
- Python复习
- 廖雪峰python3教程
- github教程
- 机器学习代码修行100天
3. 机器学习资料汇总
- 深度学习经典论文
- 深度学习斯坦福教程
- 莫烦机器学习教程
- 吴恩达机器学习新书:machine learning yearning
- 自上而下的学习路线: 软件工程师的机器学习