水声通信系统的建模和仿真-多径衰落信道

---

前言

本来第一节是加性高斯白噪声的，它的方法很简单，就是在原信号上加上一个高斯白。一般用randn函数或awgn函数。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、模型建立

在该模型中，有一个基地（或者其他舰艇）会发射声波，这里的参数如下所示：

声速	d	ro	采样频率	发射信号
1km/s	100m	30m	1e5	1e2

以上参数可以自己改动，以达到自己的需求

二、公式推导

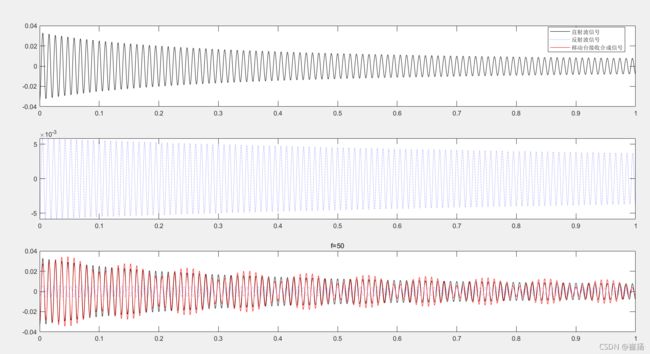
直达波、反射波和合成波公式：

E1=cos(2*pi*f.*(t-ro/c)+2*pi*fd_f*t)./(ro+v.*t);                 %%直径波信号
E2=cos(2*pi*f.*(t-(2*d-ro)/c)+2*pi*fd_z*t)./(2*d-ro+v.*t);       %%反射波信号
E3=E1-E2;                                                        %%合成信号

可以看出当v不等于0时，可以推出合成波可以近似两个不同频率的余弦波相乘，也就是在余弦波在一个余弦波的包络中，可以通过下面的仿真看出来。

---

三、仿真和结果

clc;close all;clear all;
c=1000;       %%水声的速度
f=50;         %%信号的发射频率
T=1/f;        %%信号的发射周期
v=100;        %%信号速度
fd_z=(1+v/c)*f;       %%相对方向的多普勒频率
fd_f=(1-v/c)*f;       %%相同方向的多普勒频率
ro=30;                %%与基站的距离
d=100;                %%基站与障碍物的距离
delta_t=2*(d-ro)/c;   %%直径波与反射波的时延差
fs=1e5;               %%信号采样频率
t=0:1/fs:1;           
E1=cos(2*pi*f.*(t-ro/c)+2*pi*fd_f*t)./(ro+v.*t);                 %%直径波信号
E2=cos(2*pi*f.*(t-(2*d-ro)/c)+2*pi*fd_z*t)./(2*d-ro+v.*t);       %%反射波信号
E3=E1-E2;                                                        %%合成信号
figure;
subplot(3,1,1);
F1=plot(t,E1,'-k');
subplot(3,1,2);
F2=plot(t,E2,':b');
subplot(3,1,3);
F3=plot(t,E1,'-k',t,E2,':b',t,E3,'-r');
legend('直射波信号','反射波信号','移动台接收合成信号');

四、频率选择性衰落

频率选择性衰落：信道特性随着频率不同而不同
其中时间延时差和信号周期在仿真中为：

delta_t=2*(d-ro)/c;   %%直径波与反射波的时延差
f=50;         %%信号的发射频率
T=1/f;        %%信号的发射周期

首先需要知道相干带宽是时延差的倒数
很容易可以知道：当时间延时差远小于信号周期（相干带宽远大于信号频率）时，时延差相对很小，直径波和反射波就相差不多；反之，当时间延时差远大于信号周期（相干带宽远小于信号频率）时，时延差相对很大，直径波就会被反射波验证干扰。
为了验证二者可以接着往下，写一个动态图的程序来观察这一点，其中需要将反射波和直径波分母去掉，否则二者幅值相差较大，观察现象不会很明显。这里遍了一个大致的程序，但是参数没有凑好，有兴趣的话可以自己后面再凑，如果能理解相干带宽的概念就不用。

%考虑时延差和信号周期（也就是信号频率和相干频率）
%用于判断会不会有频率选择性衰落，下面比较二者大小。
%但实际比较需要二者信号的幅值
while f<10000
    f=10+f;
    T=1/f;
    E1=cos(2*pi*f.*(t-ro/c)+2*pi*fd_f*t)./(ro+v.*t);
    E2=cos(2*pi*f.*(t-(2*d-ro)/c)+2*pi*fd_z*t)./(2*d-ro+v.*t);
    E3=E1-E2;
    delta_t=2*(d-ro)/c;
    F5=title(['反射信号和直射信号的时延差为',num2str(delta_t),',T=',num2str(T),',f=',num2str(f)]);
    set(F1,'XData',t,'YData',E1);
    set(F2,'XData',t,'YData',E2);
    set(F3,'XData',t,'YData',E3);
    drawnow;
end

总结

下面几章会从数字信号载波传输来仿真，也会将程序分享出来