动手学深度学习（PyTorch实现）笔记(正式篇1)——线性回归

动手学深度学习（PyTorch实现）笔记（正式篇1）（暂）

1. 线性回归

线性回归从零实现

• 导入包或模块

%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

• 生成数据集

num_inputs = 2                # 输入个数（特征数）
num_examples = 1000           # 数据集样本数
true_w = [2, -3.4]            # 线性回归模型真实权重
true_b = 4.2                  # 偏差
features = torch.randn(num_examples, num_inputs,
                      dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                      dtype=torch.float32)

此时，features 每一行是长度为 2 的向量；labels 每一行是长度为 1 的向量（标量）。

print(features[0], labels[0])

tensor([1.0934, 0.1052]) tensor(6.0331)

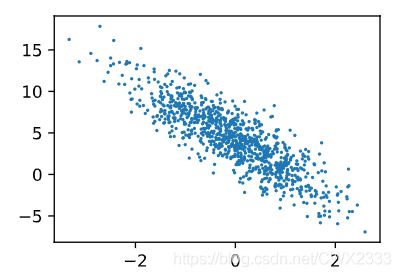
使用图像来展示生成的数据，通过生成第二个特征 features[:, 1] 和标签 labels 的散点图，更直观观察其线性关系。

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')
    
def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图尺寸
    plt.rcParams['figure.figsize'] = figsize

set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);

• 读取数据

训练模型时，需要遍历数据集并不断读取小批量数据样本。
此处定义一个函数：每次返回 batch_size （批量大小）个随机样本的特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)            # 随机读取样本
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)])
        # 最后一次可能不足一个 batch
        yield features.index_select(0, j), labels.index_select(0, j)

开始读取第一个小批量数据样本并打印。

batch_size = 10        # 批量特征形状（10，2）

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

tensor([[ 0.3239,  0.6145],
        [-0.3363, -0.3712],
        [-1.6444, -1.6122],
        [-0.4703,  2.2787],
        [-1.5904,  2.0459],
        [-0.3405, -0.0603],
        [-0.2708, -0.4437],
        [ 1.5776,  0.0512],
        [ 0.4813,  0.1332],
        [-1.9300,  0.2644]]) 
 tensor([ 2.7606,  4.7838,  6.3881, -4.4822, -5.9377,  3.7343,  5.1658,  7.1920,
         4.7004, -0.5661])

• 初始化模型参数

# 权重 初始化成 均值为0、标准差为0.01 的正态随机数
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)),
                dtype=torch.float32)
# 偏差 初始化成 0
b = torch.zeros(1, dtype=torch.float32)

此后模型训练中，需要这些参数求梯度来迭代参数的值，

因此要让它们的 requires_grad=True。

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

tensor([0.], requires_grad=True)

• 定义模型

线性回归的矢量计算表达式实现，mm()函数实现矩阵乘法。

def linreg(X, w, b):
    return torch.mm(X, w) + b

• 定义损失函数

使用均方误差损失函数。

实现中，将真实值 y 变形成预测值 y_hat 的形状。

函数返回结果也和 y_hat 的形状相同。

def squared_loss(y_hat, y):
    # 此处返回值为向量，且，pytorch的MSEloss并没有除以2
    return (y_hat - y.view(y_hat.size())) ** 2 / 2    

• 定义优化算法

sgd()函数实现 小批量随机梯度下降算法。

通过不断迭代模型参数来优化损失函数。

此处得到一个批量样本的的梯度和，除以批量大小得到平均值。

def sgd(params, lr, batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size
        # 此处更改param时用的是param.data

• 训练模型

lr = 0.03    # 学习率
num_epochs = 3    # 迭代周期个数
net = linreg
loss = squared_loss

for epoch in range(num_epochs):    # 训练模型一共需要num_epochs个迭代周期
    # 每一个迭代周期， 会使用训练数据集中所有样本一次(假设样本数能被批量大小整除)。
    # X和y分别是小批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()    # l是有关小批量X和y的损失
        l.backward()    # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size)    # 使用小批量随机梯度下降迭代模型参数
        
        # 梯度清零
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

epoch 1, loss 0.039137
epoch 2, loss 0.000154
epoch 3, loss 0.000050

比较所学到的参数与用来生成训练集的真实参数

print(true_w, '\n', w)
print(true_b, '\n', b)

[2, -3.4] 
 tensor([[ 1.9997],
        [-3.3992]], requires_grad=True)
4.2 
 tensor([4.1998], requires_grad=True)