《动手学深度学习》(Pytorch版) 学习笔记—— 3.2 线性回归的从零开始实现

---

前言

Python初学者一枚，文章仅为个人学习记录，便于以后查看使用。

本节介绍如何只利用Tensor和autograd来实现一个线性回归的训练。

首先，导入本节中实验所需的包或模块，其中的matplotlib包可用于作图，且设置成嵌入显示。

%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

1 生成数据集

构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。

设训练数据集样本数为1000，输入个数（特征数）为2。
给定随机生成的批量样本特征

我们使用线性回归模型真实权重

和偏差b=4.2，以及一个随机噪声项ϵ来生成标签：

其中噪声项ϵ服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。

下面生成数据集。

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)

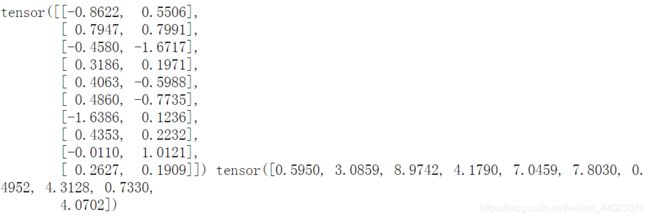
print(features[0], labels[0])

注意：features的每一行是一个长度为2的向量，而labels的每一行是一个长度为1的向量（标量）。

输出：

通过生成第二个特征features[:, 1]和标签 labels 的散点图，可以更直观地观察两者间的线性关系。

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize

# # 在../d2lzh_pytorch里面添加上面两个函数后就可以这样导入
# import sys
# sys.path.append("..")
# from d2lzh_pytorch import * 

set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);

输出：

将上面的plt作图函数以及use_svg_display函数和set_figsize函数定义在d2lzh_pytorch包里。以后在作图时，将直接调用d2lzh_pytorch.plt。
由于plt在d2lzh_pytorch包中是一个全局变量，在作图前只需要调用d2lzh_pytorch.set_figsize()即可打印矢量图并设置图的尺寸。
（原书中提到的d2lzh里面使用了mxnet，改成pytorch实现后本项目统一将原书的d2lzh改为d2lzh_pytorch。）

2 读取数据

在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。

定义一个函数：它每次返回batch_size（批量大小）个随机样本的特征和标签。

# 本函数已保存在d2lzh包中方便以后使用
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
        yield features.index_select(0, j), labels.index_select(0, j)

读取第一个小批量数据样本并打印。
每个批量的特征形状为(10, 2)，分别对应批量大小和输入个数；标签形状为批量大小。

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

输出：

3 初始化模型

权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。

w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)

之后的模型训练中，需要对这些参数求梯度来迭代参数的值，因此我们要让它们的requires_grad=True。

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

4 定义模型

下面是线性回归的矢量计算表达式的实现。
使用mm函数做矩阵乘法。

def linreg(X, w, b): # 本函数已保存在d2lzh_pytorch包中方便以后使用
    return torch.mm(X, w) + b

5 定义损失函数

使用上一节描述的平方损失来定义线性回归的损失函数。
在实现中，需要把真实值y变形成预测值y_hat的形状。
以下函数返回的结果也将和y_hat的形状相同。

def squared_loss(y_hat, y): # 本函数已保存在d2lzh_pytorch包中方便以后使用
    # 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
    return(y_hat - y.view(y_hat.size())) ** 2/2

6 定义优化算法

以下的sgd函数实现了上一节中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。
这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。将它除以批量大小来得到平均值。

def sgd(params, lr, batch_size): # 本函数已保存在d2lzh_pytorch包中方便以后使用
    for param in params:
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

7 训练模型

在训练中，将多次迭代模型参数。在每次迭代中，根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。
由于之前设批量大小batch_size为10，每个小批量的损失l的形状为(10, 1)。由于变量l并不是一个标量，所以我们可以调用.sum()将其求和得到一个标量，再运行l.backward()得到该变量有关模型参数的梯度。

注意：在每次更新完参数后不要忘了将参数的梯度清零。

在一个迭代周期（epoch）中，将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。
这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和0.03。

在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）
    # X和y分别是小批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失
        l.backward() # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
        
        # 不要忘了梯度清零
        w.grad.data.zero_()
        b.grad.data.zero_()    
    train_1 = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_1.mean().item()))

输出：

训练完成后，可以比较学到的参数和用来生成训练集的真实参数。它们应该很接近。

print(true_w, '\n', w)
print(true_b, '\n', b)

输出：

8 小结

仅使用Tensor和autograd模块就可以很容易地实现一个模型。