树系列问题III——二叉树
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
if(root == null){
return;
}
//先对二叉树进行先序遍历,然后用列表存储,再展开为单链表
List<TreeNode> node=new ArrayList<>();
PreOrder(root,node);
for(int i=0;i<node.size()-1;i++){
TreeNode NewRoot=node.get(i);
TreeNode NewRight=node.get(i+1);
NewRoot.left=null;
NewRoot.right=NewRight;
}
}
//先序遍历
public void PreOrder(TreeNode root,List<TreeNode> list){
if(root == null){
return ;
}
list.add(root);
PreOrder(root.left,list);
PreOrder(root.right,list);
}
}
结果:
执行用时:1 ms, 在所有 Java 提交中击败了36.82%的用户
内存消耗:37.5 MB, 在所有 Java 提交中击败了93.55%的用户
通过测试用例:225 / 225
124. 二叉树中的最大路径和
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
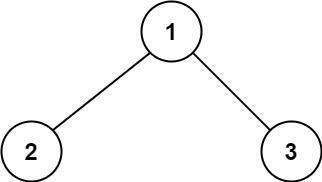
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
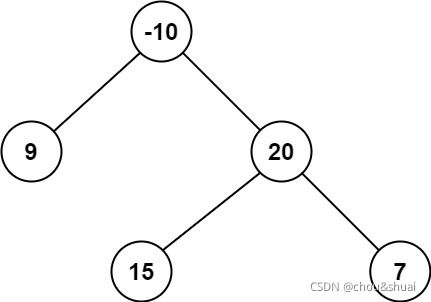
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int Maxsum=Integer.MIN_VALUE;//最大路径和
public int maxPathSum(TreeNode root) {
//对根节点调用函数 MaxPath,即可得到每个节点的最大贡献值
MaxPath(root);
return Maxsum;
}
public int MaxPath(TreeNode node){
//该函数计算二叉树中的一个节点的最大贡献值,在以该节点为根节点的子树中寻找以该节点为起点的一条路径,使得该路径上的节点值之和最大
//空节点的最大贡献值等于0;非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和
if(node == null){
return 0;
}
//递归计算左右子节点的最大贡献值
int Left=Math.max(MaxPath(node.left),0); // 只有在最大贡献值大于 0 时,才会选取对应子节点
int Right=Math.max(MaxPath(node.right),0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int pathsum=Left+node.val+Right;
//更新最大路径和
Maxsum=Math.max(Maxsum,pathsum);
// 返回节点的最大贡献值
return node.val+Math.max(Left,Right);
}
}
结果:
94 / 94 个通过测试用例
执行用时: 0 ms
内存消耗: 40.4 MB
129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
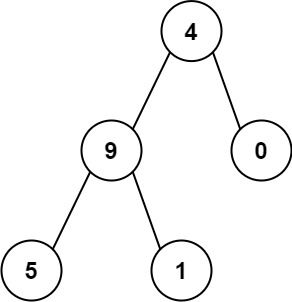
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//从根节点开始,遍历每个节点,如果遇到叶子节点,则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点,则计算其子节点对应的数字,然后对子节点递归遍历
public int sumNumbers(TreeNode root) {
return DFS(root,0);
}
public int DFS(TreeNode root,int presum){
if(root == null){
return 0;
}
int sum =presum*10+root.val;
if(root.left == null && root.right == null){
return sum;
}else {
return DFS(root.left,sum)+DFS(root.right,sum);
}
}
}
结果:
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:35.8 MB, 在所有 Java 提交中击败了61.96%的用户
通过测试用例:108 / 108
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
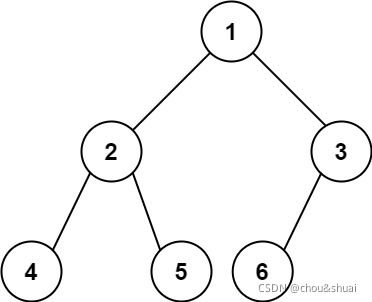
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int count=0;//记录该树的节点个数
public int countNodes(TreeNode root) {
if(root == null){
return 0;
}
Inorder(root);
return count;
}
//中序遍历,遇到节点则count++
public void Inorder(TreeNode root){
if(root == null){
return;
}
Inorder(root.left);
count++;
Inorder(root.right);
}
}
结果:
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:40.9 MB, 在所有 Java 提交中击败了45.32%的用户
通过测试用例:18 / 18