【机器学习实验一】手撕 kNN(K-Nearest Neighbor, k最邻近算法)

kNN算法

本次博客的所有源代码均已上传个人github仓库，若对您有帮助，欢迎给个star
https://github.com/Scienthusiasts/Machine-Learning

1.算法简介

kNN算法全称叫k-Nearest Neighbors，即k最近邻算法。1968年由 Cover和 Hart 提出。在机器学习算法中，kNN算法的思想简洁，可解释性强，同时也是一个有监督学习通用算法(既适用于分类问题也适用于回归问题)。不过一般情况下kNN在分类领域更为常用。

2.算法思想

kNN的思想非常容易理解：即对于一个待预测样本，该样本的类别可以用距离它最近的k个带有标签的邻居来表示：

图中X_μ为待预测点，与其最近的k个点中(k=5)，红色的点占了4个，因此该点被分类为红色。就是这么简单！

kNN算法有一个特点，那就是相对于其他分类或回归算法，kNN算法本身是无参的，不会对数据的分布做出任何假设。什么意思呢，比如说，像一般的多元线性回归或者Softmax多分类算法，算法本身是自带学习权重的，权重参数需要通过优化算法(梯度下降)学习得来，而kNN算法本身不带参数，只需要通过比较就能给出分类结果。

不过，kNN算法也并不是"一无所有"，它仍然具有两个非常重要的超参数，一个是算法的距离度量方式，另一个就是k值的选取。对于距离度量方式，最常用的就是欧式距离度量(L2)，除此之外，距离公式的选择还可以是曼哈顿距离(L1)，闵可夫斯基距离(Lp), 余弦距离等等。距离度量的选择可以根据算法实现具体任务的不同而不同。而对于K值的选取，则关系到算法的泛化能力，这一细节我们将会在后续的部分详细讨论。

3.算法流程

kNN算法的一般流程

1.计算待预测数据与各个训练数据之间的距离；
2.按照距离的递增关系进行排序；
3.选取与待预测数据距离最小前K个点；
4.确定前K个点所在类别的出现频率；
5.返回前K个点中出现频率最高的类别作为测试数据的预测分类；

伪代码

时间复杂度

由于kNN算法无需训练，因此在算法的预测过程中，时间复杂度主要来源于两方面，一是对于数据集的遍历，另一个就是距离的计算，假设数据集的size为(m,n),即包含m个数据点，每个数据的维度为n，因此距离度量产生的时间复杂度为O(n),遍历数据集产生的时间复杂度为O(m),算法的时间复杂度为两者相乘O(mn).。(忽略排序的最小时间复杂度O(mlogm))

4.代码部分

kNN算法的python实现

import numpy as np


class kNN():
    def __init__(self, k, X_train, y_train, X_test):
        self.k = k
        self.X_train = X_train
        self.y_train = y_train
        self.X_test = X_test
        self.neighbors = np.zeros((len(self.X_test), len(self.X_train)))

    # 欧氏距离
    def EuclDist(self, x0, x1):
        return np.sum(np.square(x1 - x0))

    # 计算当前数据与标签数据的距离
    def Allneighbors(self):
        for i in range(len(self.X_test)):
            for j in range(len(self.X_train)):
                self.neighbors[i, j] = self.EuclDist(self.X_test[i], self.X_train[j]) # 计算欧式距离

    # 下标转为类别(分类问题)
    def index2label(self, index):
        knearest = self.y_train[index][:self.X_test.shape[0]] # 获取下标对应的标签
        # 统计K近邻的大多数:
        predict = []
        for i in range(self.X_test.shape[0]):
            predict.append(np.argmax(np.bincount(knearest[i]))) # 统计出现次数最多的类别
        return np.array(predict)

    # 下标转为数值(回归问题)
    def index2value(self, index):
        knearest = self.y_train[index][:self.X_test.shape[0]] # 获取下标对应的标签
        # 统计K近邻的大多数:
        predict = np.mean(knearest, axis=1) # 预测结果为k近邻的均值
        return predict.reshape(-1)

    # kNN算法主干
    def kNN(self, mode="classification"):
        # 1.计算距离
        self.Allneighbors() 
        # 2.按距离从小到大排序
        self.sort_index = np.argsort(self.neighbors, axis=1, kind='quicksort', order=None) 
        # 3.取前k个近邻
        self.sort_index = self.sort_index[:, 0:self.k] 
        # 4.确定前K个点所在类别的出现频率
        # 5.返回前K个点中出现频率最高的类别
        if mode == "classification":   # 分类
            return self.index2label(self.sort_index)
        if mode == "regression":       # 回归
            return self.index2value(self.sort_index)

kNN实现手写数字分类(书上的例子)

使用书本上的例子,原始文件采用txt文本文件以二值化01存储：

将原始文件压缩为(batches, h, w)的numpy矩阵格式转储：

def txt2img(path):
    X, y = [], []
    for files in os.listdir(path):
        file = open(path + files)
        data = []
        for line in file.readlines():
            row = []
            for pix in line[:-1]:
                row.append(int(pix))
            data.append(np.array(row))
        X.append(np.array(data))
        y.append(int(files.split('_')[0]))

    return np.array(X), np.array(y)


path = './testDigits/'
X, y = txt2img(path)
np.save('X_test.npy', X)
np.save('y_test.npy', y)

digit_recognize.py

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split  # 划分训练集和验证集

# 导入自定义评估模块:
import sys; sys.path.append('../')
from kNN import kNN
sys.path.append('../../metrics')
from metrics import metrics



# 读取数据集
X_train = np.load('X_train.npy')
y_train = np.load('y_train.npy')
X_test = np.load('X_test.npy')
y_test = np.load('y_test.npy')


# 数据集可视化
for i in range(32):
    plt.subplot(4, 8, i+1)
    img = X_train[i*60,:]
    plt.imshow(img)
    plt.title(y_train[i*60])
    plt.axis("off")                
    plt.subplots_adjust(hspace = 0.3)  # 微调行间距
plt.show()



# KNN最近邻进行分类
knn = kNN(3, X_train, y_train, X_test)
pred = knn.kNN()
# 分类准确率
accuracy = np.mean(pred == y_test)
print(pred.shape)
print('准确率:', accuracy)

准确率: 0.9894291754756871

kNN实现约会网站配对(书上的例子)

读取约会数据集并可视化

# 读取约会数据集
def draw(X, y):
    # 数据集3D可视化
    fig = plt.figure()
    # 3D绘图
    ax = fig.add_subplot(111, projection='3d')
    # 按类别分类
    X_sort = [np.where(y==i+1) for i in range(3)]
    color = ["red", "green", "blue"]
    label = ["不喜欢", "一般", "极具魅力"]
    for i in range(3):
        ax.scatter(X[X_sort[i], 0], X[X_sort[i], 1], X[X_sort[i], 2], s=5, c=color[i], label=label[i]) 
        ax.legend()
    plt.show()

if __name__ == '__main__':
    path = './datingTestSet2.txt'
    # 读取数据
    X, y = read_datasets(path)
    # 划分训练集验证集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
    # 标准归一化
    scaler = StandardScaler()
    scaler.fit(X_train)
    X_train = scaler.transform(X_train)
    X_test  = scaler.transform(X_test)
    # 数据集3D可视化
    draw(X_train, y_train)

kNN最近邻分类：

    # KNN 最近邻进行分类
    knn = kNN(10, X_train, y_train, X_test)
    pred = knn.kNN()
    # 分类准确率
    accuracy = np.mean(pred == y_test)
    print(pred.shape)
    print('准确率:', accuracy)

准确率: 0.9533333333333334

kNN实现手写数字分类(sklearn的例子)

数据集来源：sklearn.datasets.load_digits

sklearn 是python下的一个机器学习库，本次数据集使用sklearn下自带的手写数字数据集：load_digits

和家喻户晓的MNIST数据集相比，sklearn下的手写数字是8x8大小，数据集的特征维度有所减少。

数据集信息：

Each datapoint is a 8x8 image of a digit.

================= ==============

Classes 10

Samples per class ~180

Samples total 1797

Dimensionality 64

================= ==============

数据集部分可视化

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as datasets  # 数据集模块

# 读取数据集
X, y = datasets.load_digits(return_X_y=True)


for i in range(32):
    plt.subplot(4, 8, i+1)
    img = X[i,:].reshape(8, 8)
    plt.imshow(img)
    plt.title(y[i])
    plt.axis("off")                
    plt.subplots_adjust(hspace = 0.3)  # 微调行间距
plt.show()

预测，计算accuracy

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as datasets  # 数据集模块
from sklearn.model_selection import train_test_split  # 划分训练集和验证集

from kNN import kNN
# 读取数据集
X, y = datasets.load_digits(return_X_y=True)
# 随机划分训练集和验证集,使用sklearn中的方法
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# KNN最近邻进行分类(k=6)
knn = kNN(6, X_train, y_train, X_test)
pred = knn.kNN()
# 分类准确率
accuracy = np.mean(pred == y_test)
print('准确率:', accuracy)

准确率: 0.9805555555555555

可以看到算法的识别准确率还是比较可观的，然而代价就是算法需要将每一个样本点与训练集数据一一进行距离的计算，时间复杂度大约在O(nm)。

预测结果评估，可视化混淆矩阵(k = 200)，计算precision， recall值

class metrics():

    '''混淆矩阵可视化'''
    # y_hat.shape = [datasize,]
    # y.shape = [datasize,]
    # label.shape = [classes,]
    @staticmethod 
    def confusion_matrix_vis(y, y_hat, label):
        conf_mat = confusion_matrix(y, y_hat)
        # print(conf_mat)
        df_cm = pd.DataFrame(conf_mat, index = label, columns = label)
        heatmap = sns.heatmap(df_cm, annot = True, fmt = 'd', cmap = "hot")
        heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation = 0, ha = 'right')
        heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation = 50, ha = 'right')
        plt.ylabel('Ground Truth')
        plt.xlabel('Prediction')
        plt.show()


    '''评估分类模型的查准率与召回率'''
    @staticmethod 
    def precision_recall(y, y_hat, classes):
        conf_mat = confusion_matrix(y, y_hat)
        # total_num = np.sum(conf_mat)

        TP = [conf_mat[i,i] for i in range(classes)]
        FP = [np.sum(conf_mat[:,i]) - TP[i] for i in range(classes)]
        FN = [np.sum(conf_mat[i,:]) - TP[i] for i in range(classes)]
        # TN = [total_num - FN[i] - FP[i] - TP[i] for i in range(classes)]

        precision = [TP[i] / (TP[i] + FP[i]) for i in range(classes)]
        recall = [TP[i] / (TP[i] + FN[i]) for i in range(classes)]

        return precision, recall



label = [0,1,2,3,4,5,6,7,8,9]
# 绘制混淆矩阵
metrics.confusion_matrix_vis(y_test, pred, label)
precision, recall = metrics.precision_recall(y_test, pred, 10)
for i in range(10):
    print('类别%d: 查准率:%f, 召回率:%f' % (i, precision[i], recall[i]))

(540,)
准确率: 0.8907407407407407
类别0: 查准率:0.963636, 召回率:0.981481
类别1: 查准率:0.847826, 召回率:0.709091
类别2: 查准率:0.808511, 召回率:0.950000
类别3: 查准率:0.892857, 召回率:0.980392
类别4: 查准率:0.920635, 召回率:0.906250
类别5: 查准率:0.934783, 召回率:0.843137
类别6: 查准率:0.906250, 召回率:0.983051
类别7: 查准率:0.910448, 召回率:0.968254
类别8: 查准率:0.953488, 召回率:0.788462
类别9: 查准率:0.754717, 召回率:0.784314

5.实验部分

数据归一化对预测精度的影响(基于约会网站的例子)

一般情况下，机器学习算法对于输入的数据都有一个普遍的要求，那就是输入数据的量纲必须尽可能的一致，即输入特征不同特征维度之间的尺度范围应尽量保持一致。

在约会网站的例子中，每年获得的飞行常客里程数与其他维度的量纲存在数量级别的差距，因此在计算过程中，量纲较大的维度的损失将主导数据的总损失(损失类比kNN的距离计算)，宏观来看就是，数据的分布在量纲大的维度十分突出，其余的维度分布不明显，仿佛数据被降维了：

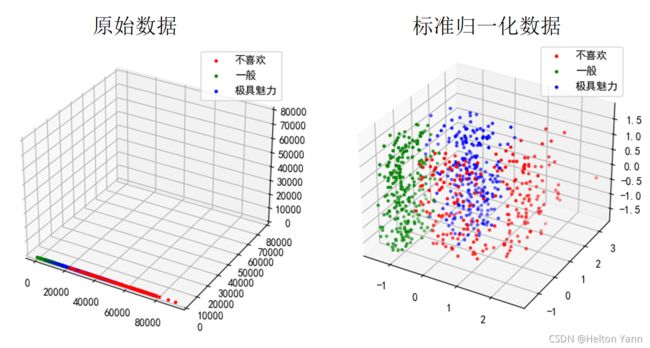
经过多次实验，未归一化数据与归一化数据在预测精度上的比值大约在0.83左右(k=200)：

… …
未归一化准确率: 0.8033333333333333
归一化后准确率: 0.96
比值：0.8368055555555556
… …

可见，数据归一化能够提升kNN算法的预测精度。

k的取值对决策的影响

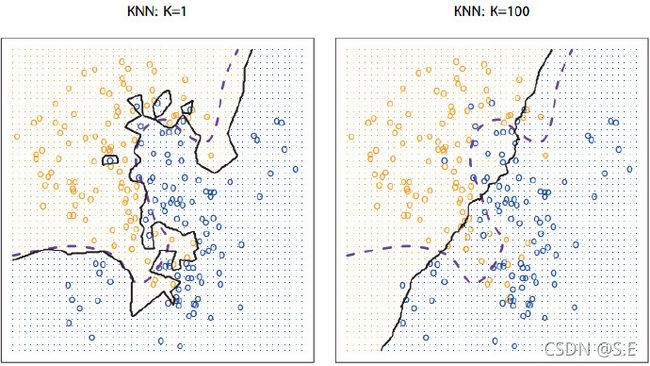
在算法思想部分我们稍微提到了kNN算法一个非常重要的超参数k，k的值决定了算法做出最终决策需要参考的近邻数，由于k是算法的一个超参，因此我们可以通过将k的值设置为一个自变量，通过绘制k-acc曲线来寻找一个比较合适的k值：

实验结论

上面这张图仍然是基于sklearn.datasets.load_digits数据集所绘制的，实验采取将数据集以4：1的比例划分为训练集和验证集，横轴表示算法的k的取值(1-100)，纵轴表示最终验证集的识别准确率。实验表明，当k的取值在5左右时，算法会有较好的准确率，当k值逐渐增大时，准确率明显呈现下降的趋势。

一个可能的解释是k值反映了kNN模型的复杂程度，这个解释实际上是相对于有参机器学习算法而言。

k值越小，代表模型的‘感受野’越小，待分类数据对于近邻数据的依赖程度也就越大，模型也就越复杂。一旦近邻数据存在噪声或是特征不够一般，模型就有极大的概率出错。这在有参机器学习上实则是一个过拟合概念。

相反的，k值越大，模型的‘感受野’也就越大，待分类数据对于近邻数据的依赖程度也就越小(因为参与决策的数据增多了），这时候表示模型越简单，比较不容易受到异常点或是噪声的影响，模型的泛化能力更好。然而实验结果表明k值也不能太大，k值越大，模型的归纳能力也就越差，这实际上也一种欠拟合现象。一个极端的情况是，当k值等于训练样本数时，对于任意输入样本，模型的决策都相同，这时候模型的归纳能力为0

对于上面的描述，使用一个可视化的例子可能会更直观些：

上面的图示中，我使用kNN算法来完成一个函数回归任务(回归方法为取k近邻的均值)，每一张图表示一个等高线地形图，每张图的采样点均为2500。

待预测函数：
$$f(x,y)=\sin \left(\sqrt{x^2+y^2}\right)+\cos (x)$$
左侧的GT表示函数的真值，右侧依次表示当k=(1, 50, 300, 500, 1000, 2000, 2300, 2500)时算法的回归效果。可见随着k值的增大，算法预测结果越“平滑”，预测样本之间的特征也越相似。当k=2500时，算法相当于求取数据点的均值，所有数据点被回归到了同样的值。

实验代码

生成回归数据：

import numpy as np
import matplotlib.pyplot as plt

class datasets():

    def F(self, x, y):
        return np.sin(np.sqrt(x**2 + y**2)) + np.cos(x)

    def gen_data(self):
        # 生成x,y的数据
        n = 50
        x, y = np.linspace(-30, 30, n), np.linspace(-30, 30, n)
        # 把x,y数据生成mesh网格状的数据
        X, Y = np.meshgrid(x, y)
        Z = self.F(X, Y)

        x = X.reshape(-1, 1) 
        y = Y.reshape(-1, 1)
        z = Z.reshape(-1)
        data = np.c_[x, y]
        
        return X, Y, Z, data, z

预测与数据可视化：

def save_prediction():
    # 读取数据集
    data = datasets()
    X_grid, Y_grid, Z, X, y = data.gen_data()
    # 划分训练集和验证集,使用sklearn中的方法
    # KNN最近邻进行分类
    knn = kNN(1, X, y, X)
    pred = knn.kNN(mode="regression").reshape(50, 50)
    np.save('k=1.npy', pred)

def k_regression_visualize():
    k = ['1', '50', '300', '500', '1000', '2000', '2300', '2500']
    data = datasets()
    X_grid, Y_grid, Z, _, _ = data.gen_data()

    plt.figure(figsize=(26, 13))
    for i in range(8):
        plt.subplot(2,4,i+1)
        plt.title('k='+k[i])
        pred = np.load('k='+k[i]+'.npy')
        contour = plt.contourf(X_grid, Y_grid, pred, 100, cmap='bwr')
        plt.colorbar(contour)
    plt.subplots_adjust(left=0.02,bottom=0.05,right=0.98,top=0.95,wspace=0.07,hspace=0.1)
    plt.savefig('./kNN.png',dpi=100)
    # plt.show()

6.算法优缺点总结

优点：

算法简洁，易于理解，可解释性强。

kNN属于一种惰性算法，因此不需要训练。

缺点：

算法需要在内存中存储所有的数据集，内存占用高

算法预测阶段的时间复杂度高，存在维度灾难问题

对k值敏感，超参数k不好确定

机器学习实验专栏系列文章：
【机器学习实验一】手撕 kNN(K-Nearest Neighbor, k最邻近算法)
【机器学习实验二】决策树(Decision Tree)及其在图像识别任务上的应用
【机器学习实验三】纯手撕三种朴素贝叶斯算法(Naive Bayes)，并进行IMDB影评数据集分类及手写数字识别