SVO原理解析
文章目录
-
- 一、SVO框架:
- 二、定位
-
- 1、稀疏图像对齐
- 2、特征点对齐
- 3、地图优化(位姿及点云结构优化)
- 三、建图
- 四、深度滤波器:《Video-based, Real-Time Multi View Stereo》
- 五、参考文献
一、SVO框架:

从上图可以看出SVO的分为两个主要部分:定位和建图。这两部分以并行线程执行,保证算法的实时性。从图中也可以看出来,两个线程是有所耦合的,如定位线程的第二步(图像坐标对齐)时使用了建图中估计的特征点的深度(三维坐标点)。
SVO算法分解开后,就是几个比较传统的求解思路的组合。
定位中包含三步:
1、 直接法求解粗略的相机初始位姿:这里作者不再使用大范围的图像块进行直接法的tracking,进在关键帧进行离散的特征点提取,并保证特征点在图像中分布的均匀性。将特征点按帧进行传递,使用特征点及其周围的图像块(4*4)进行灰度值匹配来实现直接法求解。
2、 光流法优化3D点的投影坐标:光流法得到空间点在当前帧的投影坐标,从而将问题转化为普通的特征点法的求解问题。
3、 特征点法,使用Local BA优化。这一步就是传统的特征点法的求解思路,已知两帧图像的特征点的图像坐标,求解相机位姿及特征点的三维坐标。
也就是说SVO是直接法、光流法及特征点的综合算法了。
Tips:
作者自身也讨论了,如果不用第一步,直接使用第二步和第三步也可以实现定位(这样就是LK-slam的求解思路了),作者给出的原因,如果不使用第一步直接法得到比较可靠的相机位姿,直接使用第二步寻找匹配点,那么会使得求解过程比较长,且不能很好的判断外点(计算错误的一些空间点)。
此外,如果只用第一步直接法,则会有比较大的漂移。
建图:
建图中包含了点云的深度估计,单目深度估计大多采用概率模型的滤波方法来实现深度的估计,就是假设点的深度符合一定的概率模型,在得到新的观测值后,对点的深度的估计进一步调整,当深度的方差小于一定的阈值之后,说明该点的深度估计值比较可靠,进而参与帧间传递,并最终加入环境地图中。
作者这里的点云深度概率模型是高斯+均匀分布。
二、定位
1、稀疏图像对齐
通过最小化与相同3D点的投影位置对应的像素之间的光度误差,得到相机相对于前一帧 k − 1 k-1 k−1时刻的位姿变化 T k , k − 1 T_{k,k-1} Tk,k−1。在图中,红色部分指的是待求解的参数,蓝色表示需要优化的约束。下同。
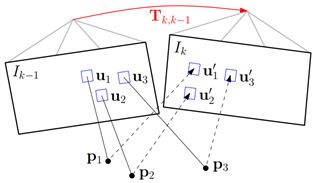
注意:只有关键帧才会进行特征点提取,不是关键帧,则通过新的普通帧的观测,优化特征点的深度值,然后将特征点传播给当前帧。
误差公式: k − 1 k-1 k−1帧图像特征点 u i \mathbf{u}_i ui及其周围像素块的灰度与其对应点及其周围像素块在 k k k帧图像所呈现的灰度值相等。
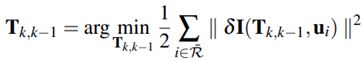
其中:
![]()
I ( u i ) {\mathbf{I}}(\mathbf{u}_i) I(ui)表示特征点及其周围点形成的特征点patch,设为 4 × 4 4\times4 4×4的围绕该特征点的像素。
这一步的优化,作者使用了Inverse Compositional的求解方法,使雅可比矩阵固定,可离线求解。注意IC法是对 I k − 1 \mathbf{I}_{k-1} Ik−1进行展开求导。IC方法雅可比矩阵固定。ICInverse Compositional介绍
J = J= J=
下降方向求解:
![]()
其中的 δ I ( 0 ) \delta\mathbf{I}(0) δI(0)是指 δ I ( 0 , u i ) \delta\mathbf{I}(0, \mathbf u_i) δI(0,ui), p i \mathbf{p}_i pi是指 k − 1 k-1 k−1帧的相机坐标系下与 u i \mathbf{u}_i ui对应的空间点在 k − 1 k-1 k−1帧相机坐标系下的三维坐标。IC方法每次迭代,雅可比矩阵不需要重新计算,只需要计算 δ I ( 0 ) \mathbf{\delta}\mathbf{I}(\mathbf{0}) δI(0),然后求解下降方向 ξ \mathbf{\xi} ξ。
定位 T k , k − 1 T_{k,k-1} Tk,k−1更新:注意IC反向求解,累加 T ( ξ ) − 1 {T(\mathbf{\xi})}^{-1} T(ξ)−1。
![]()
2、特征点对齐
上一步得到 T k , k − 1 T_{k,k-1} Tk,k−1,以及估计的图像特征点深度(由mapping线程得到),但是不准确的位姿及点云深度估计会给带来匹配误差,如下图所示,通过光度误差,优化特征点在当前( k k k)帧的投影图像坐标。注意,特征点只有在关键帧才提取。
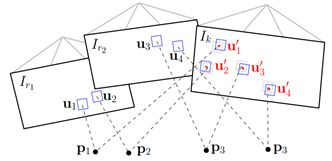
误差方程:对于当前帧能够观测到的每个特征(空间)点,找到能够观测该点的最近的关键帧,这里使用的是观测角度大小来评价。约束关键帧的特征点块与当前帧的匹配的特征点块的光度误差来找到更加准确的空间点在当前帧k帧的图像坐标。
由于使用关键帧来进行光度约束匹配,因此距离较远,且选择的图像块较大,使用(8*8),因此,作者同时加了映射变换 A i A_i Ai来保证匹配的合理性,这个映射变换通常用来对图像块进行拉伸以及旋转等变换。
由于没有变换矩阵 T T T的参与,直接优化 u u u则会使得最后的结果小部分偏离极线约束。
求解:同样使用IC(inverse compositional)来求解,上述问题成为一个光流法中求解匹配点的步骤,使用LK的IC求解得到 u i ′ \mathbf{u}_i\prime ui′。
3、地图优化(位姿及点云结构优化)
以上得到当前帧特征点的在当前图像上的投影图像坐标 u i ′ \mathbf{u}_i\prime ui′,便可以使用类似特征点法的思路来优化位姿估计,再固定位姿估计,进一步优化3D点的位置。这一步有两个优化步骤:1)优化相机位姿估计;2)优化3维点世界坐标。

约束方程:
- 位姿估计约束方程:已知两帧(临近关键帧 r r r与当前帧 k k k)之间的匹配特征点的图像坐标,求解相机运动,这就是传统特征点法求解的问题,约束就是已知的特征点提图像投影坐标和使用变换矩阵 T T T得到的图像坐标之间的差值。
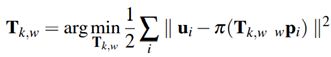
- 3维空间点位置优化:

这个问题就是一个local BA的问题,同普通的特征点法一致,可以使用g2o等工具,通过添加点面约束进行求解。
三、建图
建图部分:作者将特征点提取及深度估计作为建图的内容。
首先判断是否为关键帧,当观测到附近的观测帧都距离当前帧较远则将当前帧作为关键帧。
代码文件:
svo/src/frame_handler_mono.cpp: fuction: FrameHandlerMono::processFrame()
186 double depth_mean, depth_min;
187 frame_utils::getSceneDepth(*new_frame_, depth_mean, depth_min);
188 if(!needNewKf(depth_mean) || tracking_quality_ == TRACKING_BAD)
189 {
190 depth_filter_->addFrame(new_frame_);
191 return RESULT_NO_KEYFRAME;
192 }
193 new_frame_->setKeyframe();
194 SVO_DEBUG_STREAM("New keyframe selected.");
-
当前帧为关键帧:初始化深度滤波器。
将已经收敛的尚未插入地图中点(point_candidates_)以及地图中能够在当前帧下观测到的点都插入到当前帧中,并进行新一轮的特征点检测。为每一个构建的特征点,均构建深度种子,深度方差初始化为一个较大值。深度值初始化为由先前传递过来的三位点的深度的平均值。就是尚未插入地图中点(point_candidates_)以及地图中能够在当前帧下观测到的点。 -
当前帧是普通帧:估计迭代特征点深度,当深度估计方差小于一定阈值,表明深度估计收敛,则插入地图。
使用定位线程得到的 T r , k T_{r,k} Tr,k,计算得到参考关键帧 r r r中的点 u i \mathbf{u}_i ui对应到当前帧k图像中极线,根据定位线程得到的当前帧关于 u i \mathbf{u}_i ui的匹配点 u i ′ \mathbf{u}_i\prime ui′,则可以利用三角化计算处 u i ′ \mathbf{u}_i\prime ui′对应的深度值 d i k ~ \widetilde{d_i^k} dik 。作者设 d i k ~ \widetilde{d_i^k} dik 符合高斯+均匀分布:
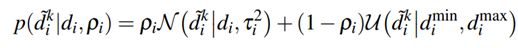
其中 ρ i \rho_i ρi表示预测点是内点的概率
内点表示估计较为可靠时, d i k ~ \widetilde{d_i^k} dik 服从以真实深度 d i d_i di为均值, τ i 2 \tau_i^2 τi2为方差的正态分布。
外点则表示该点是不可靠的点,此时,设, d i k ~ \widetilde{d_i^k} dik 服从 [ d i m i n , d i m a x ] [d_i^{min},d_i^{max}] [dimin,dimax]的均匀分布。
d i m i n d_i^{min} dimin和 d i m a x d_i^{max} dimax根据估计值与方差取的。
SVO的深度滤波器使用的概率模型是《Video-based, Real-Time Multi View Stereo》中的深度概率模型,不同的是SVO中的使用的逆深度估计。
四、深度滤波器:《Video-based, Real-Time Multi View Stereo》
由于单目直接法匹配会产生一些错误的结果,单一的模型分布,如高斯很难收敛,且不具备检测外点的功能,因此一种混合模型被提出,这个模型考虑外点,即在极线上找不到其对应的匹配点,不过极线的搜索准确的前提是相机的位姿足够精确的基础上。概率模型如下所示:(1)
p ( x n ∣ Z , π ) = π N ( x n ∣ Z , τ n 2 ) + ( 1 − π ) U ( x n ∣ Z m i n , Z m a x ) p\left(x_n|Z,\pi\right)=\pi N\left(x_n|Z,\tau_n^2\right)+\left(1-\pi\right)U\left(x_n|Z_{min},Z_{max}\right) p(xn∣Z,π)=πN(xn∣Z,τn2)+(1−π)U(xn∣Zmin,Zmax)
其中, x n x_n xn表示第 n n n次观测得出的深度计算值;
Z Z Z表示此点对应的真实深度;
π \pi π表示该点是内点的概率。
上述概率模型是说,当特征点为内点时,该点的观测值深度结果是以真实深度为中心, τ 2 \tau^2 τ2为方差的正态分布,当特征点不为内点时,即该点可能由于计算错误,并不属于参考帧的观测范围等等原因,则该点的观测值深度结果服从一个区间的均匀分布。
我们需要根据一序列的特征点的观测结果 x 1 x_1 x1, ⋯ x n \cdots x_n ⋯xn,来最大可能的拟合出该特征点的真实深度。即使下述概率最大:
p ( Z , π ∣ x 1 , ⋯ , x n ) p\left(Z,\pi|x_1,\cdots{,x}_n\right) p(Z,π∣x1,⋯,xn)
一种思路就是,将可能的Z分为一些等分,将所有的观测结果对应落入 Z Z Z的格子中,形成直方图的形式:如下分别对应5, 10, 20, 100次的计算结果,横轴表示 Z Z Z的分布,就是将可能的深度值分格排列在横轴上,纵轴表示有多少次的观测深度落在此深度格中。
![]()
这是一种计算方法,但是要对所有的特征点都进行深度估计,每个点的深度估计想要越精确,则深度的分格对应就越小,则对应的可能深度值就多(就是指横轴分布的越细越宽),这样非常耗存储,并且并不能应对外点的情况。
因此作者提出了参数化混合概率模型求解的方法。利用概率密度函数迭代收敛来得到深度估计值,同时加入了内点因子 π \pi π来排除外点干扰。
概率模型迭代:每次观测之后,利用新观测值对深度概率模型进行更新:

其中: C C C为常数,

内点概率 π \pi π符合Beta分布。这个理解,是否为内点设定符合二项分布,即由发生的次数和未发生的次数,即如果 a + b a+b a+b次观测中, a a a次观测为内点, b b b次观测为外点,则内点概率 π = a a + b \pi=\frac{a}{a+b} π=a+ba,则 a a a, b b b决定\pi的值,则 π \pi π符合 B e t a ( a , b ) Beta(a,b) Beta(a,b)分布。二项分布的概率符合Beta分布。
公式(2)的推导:
设 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn相互独立,即 p ( x i ∣ x j ) = p ( x i ) , p ( x i , x j ) = p ( x i ) p ( x j ) p(x_i|x_j)=p(x_i), p(x_i,x_j)=p(x_i)p(x_j) p(xi∣xj)=p(xi),p(xi,xj)=p(xi)p(xj)
其他涉及公式: p ( x , y ) = p ( x ∣ y ) p ( y ) p(x,y)=p(x|y)p(y) p(x,y)=p(x∣y)p(y)

有了迭代公式,如何计算出 p ( Z , π ∣ x 1 , ⋯ x n ) p\left(Z,\pi|x_1,\cdots x_n\right) p(Z,π∣x1,⋯xn)?
令:
![]()
即:
![]()
根据公式(2)可知深度估计分布的更新公式:

其中:
C p ( Z , π ∣ a n − 1 , b n − 1 , μ n − 1 , σ n − 1 ) p ( x n ∣ Z , π ) Cp\left(Z,\pi|a_{n-1},b_{n-1},\mu_{n-1},\sigma_{n-1}\right)p\left(x_n|Z,\pi\right) Cp(Z,π∣an−1,bn−1,μn−1,σn−1)p(xn∣Z,π)不再服从×分布,则使用矩匹配让其近似于×分布。
使用矩相等求得更新后的概率模型参数 a n , b n , μ n , σ n a_n,b_n,\mu_n,\sigma_n an,bn,μn,σn
1)首先计算Gaussian* Beta分布的一阶矩和二阶矩:(*1)
Z的一阶矩:
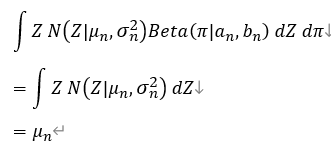
Z的二阶矩:
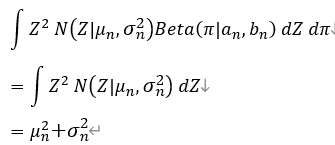
π \pi π的一阶矩:

π \pi π的二阶矩:
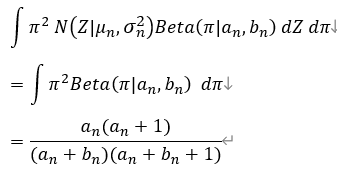
上式可以看出一阶矩对应概率参数的期望,二阶(非中心)矩就是对变量的平方求期望,二阶中心矩对应变量方差。通过使矩相等,近似分布。并通过观测值更新深度概率模型。
2)计算叠加新的观测值后的深度概率 C p ( Z , π ∣ a n − 1 , b n − 1 , μ n − 1 , σ n − 1 ) p ( x n ∣ Z , π ) Cp\left(Z,\pi|a_{n-1},b_{n-1},\mu_{n-1},\sigma_{n-1}\right)p\left(x_n|Z,\pi\right) Cp(Z,π∣an−1,bn−1,μn−1,σn−1)p(xn∣Z,π)的矩:
首先计算新的观测概率模型:
![]()
叠加带入公式(4) 得到新的深度概率模型:

利用以下公式将上步公式中 Z Z Z分离,方便后续求矩的积分:
![]()
证明过程如下:
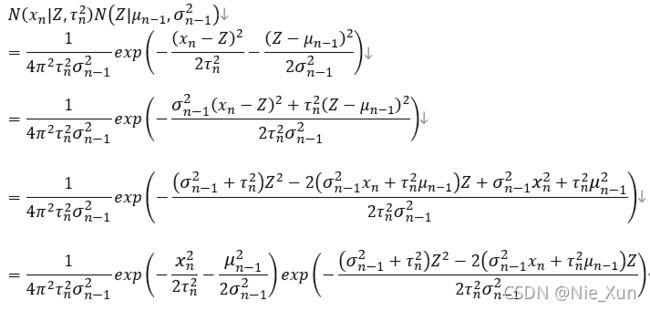
令:

上式凑平方可化为:

(6)代入以上公式(5):
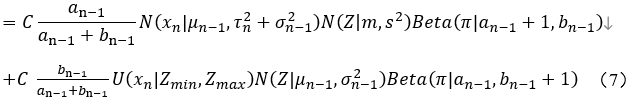
令:
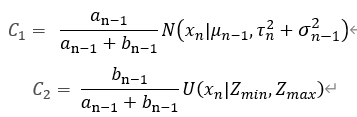
接着公式(7)简化:
![]()
使 p ( Z , π ∣ a n , b n , μ n , σ n ) p\left(Z,\pi|a_n,b_n,\mu_n,\sigma_n\right) p(Z,π∣an,bn,μn,σn)归一化,即要满足概率密度0阶矩为1:
![]()
即:

所以:
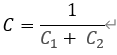
对应上文中的 N = C 1 + C 2 {N=C}_1+{\ C}_2 N=C1+ C2
令:

最后(8)变为:
![]()
开始根据(9)计算一阶矩和二阶矩**(*2)**
Z的一阶矩:

Z的二阶矩:

π \pi π的一阶矩:
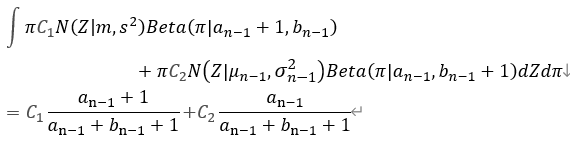
π \pi π的二阶矩:
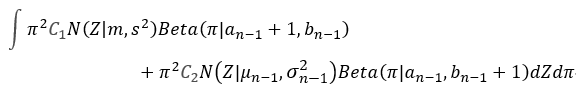
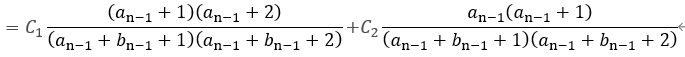
利用以上更新后的一二阶矩的值 (*2),对应 (*1),求得更新后的概率模型参数 ( a n , b n , μ n , σ n ) \left(a_n,b_n,\mu_n,\sigma_n\right) (an,bn,μn,σn)

令:
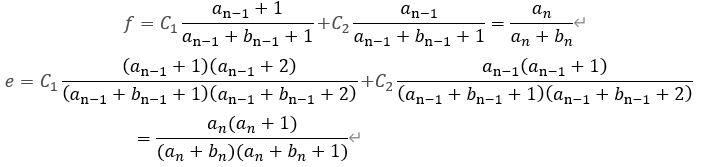
得:

代入上式:

整理:

附代码程序:svo/ src/depth_filter.cpp updateSeed()
309 void DepthFilter::updateSeed(const float x, const float tau2, Seed* seed)
310 {
311 float norm_scale = sqrt(seed->sigma2 + tau2);
312 if(std::isnan(norm_scale))
313 return;
314 boost::math::normal_distribution<float> nd(seed->mu, norm_scale);
315 float s2 = 1./(1./seed->sigma2 + 1./tau2);
316 float m = s2*(seed->mu/seed->sigma2 + x/tau2);
317 float C1 = seed->a/(seed->a+seed->b) * boost::math::pdf(nd, x);
318 float C2 = seed->b/(seed->a+seed->b) * 1./seed->z_range;
319 float normalization_constant = C1 + C2;
320 C1 /= normalization_constant;
321 C2 /= normalization_constant;
322 float f = C1*(seed->a+1.)/(seed->a+seed->b+1.) + C2*seed->a/(seed->a+seed->b+1.);
323 float e = C1*(seed->a+1.)*(seed->a+2.)/((seed->a+seed->b+1.)*(seed->a+seed->b+2.))
324 + C2*seed->a*(seed->a+1.0f)/((seed->a+seed->b+1.0f)*(seed->a+seed->b+2.0f));
325
326 // update parameters
327 float mu_new = C1*m+C2*seed->mu;
328 seed->sigma2 = C1*(s2 + m*m) + C2*(seed->sigma2 + seed->mu*seed->mu) - mu_new*mu_new;
329 seed->mu = mu_new;
330 seed->a = (e-f)/(f-e/f);
331 seed->b = seed->a*(1.0f-f)/f;
332 }
333
五、参考文献
[1] Forster C , Pizzoli M , D Scaramuzza∗. SVO: Fast semi-direct monocular visual odometry[C]// IEEE International Conference on Robotics & Automation. IEEE, 2014.
[2] G. Vogiatzis and C. Hernandez, “Video-based, Real-Time Multi View ´
Stereo,” Image and Vision Computing, vol. 29, no. 7, 2011
3.https://www.cnblogs.com/ilekoaiq/p/8228324.html
4.https://www.zybuluo.com/Xiaobuyi/note/1107128
5.depth_filter.pdf来自泡泡