广义相加模型(GAM)与向前逐步选择算法(基于R语言)
广义相加模型(GAM)与向前逐步选择算法(基于R语言)
一、题目
(a)使用College数据集,以Outstate作为响应变量,其余作为预测变量,使用逐步回归得到一组合适的预测变量的子集。
(b)将观测数据分成训练集和测试集。在训练集上拟合广义可加模型,将Outstate作为响应变量,逐步回归得到的结果作为预测变量。画出拟合结果,解释你的发现。
(c)在测试集上评价前面得到的模型,并解释结果。
(d)如果有的话,观察哪些变量和响应变量有非线性关系。
二、向前逐步选择
导入college数据集后,先进行数据的预处理。
分类变量Private需改成数值型的0-1变量,便于线性回归。
数据集的第一列是大学名称,对于预测Outstate没有帮助,所以删去。(下列代码基于R语言)
library(data.table)
college = fread("C:\\Users\\39291\\Downloads\\College.csv", data.table = FALSE)#导入数据
college$Private = as.numeric(as.factor(college$Private)) - 1#将分类变量Private的Yes改成1,No改成0
college = college[, -1]#删去数据框的第一列
进行向前逐步回归,也就是根据RSS最低原则,不断增加预测变量的个数,得到不同预测变量个数的RSS较低的模型。
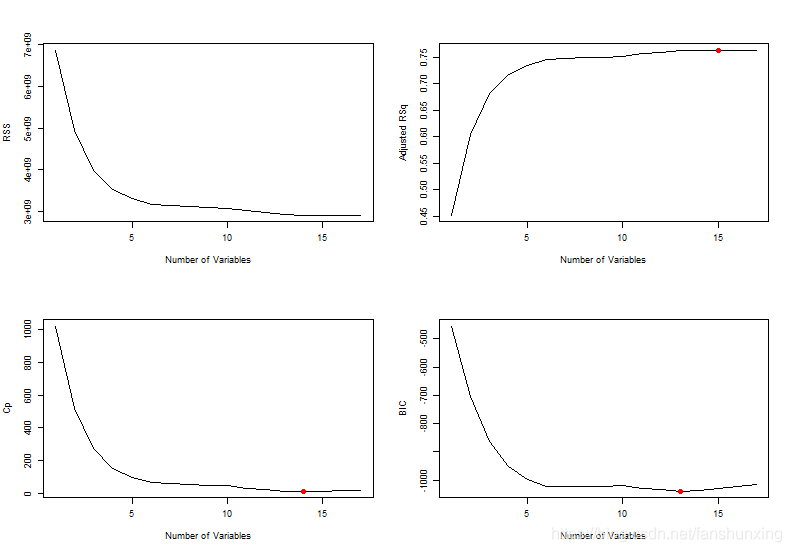
画出RSS与预测变量的关系,显然随着预测变量的增加,RSS单调减少。
画出调整后R2、Cp、BIC与模型预测变量个数的关系,并根据这三个准则选取最优模型。
library(leaps)
regfit.fwd = regsubsets(Outstate ~ ., data = college, nvmax = 18, method = "forward") #向前逐步回归
par(mfrow = c(2, 2)) #告诉R:我要画一张带有4张子图的图片,每行两张图,共两列。
plot(summary(regfit.fwd)$rss, xlab = "Number of Variables", ylab = "RSS", type = "l") #画出RSS与变量个数的关系图
plot(summary(regfit.fwd)$adjr2, xlab = "Number of Variables", ylab = "Adjusted RSq",
type = "l") #画出调整后R2与变量个数的曲线图
which.max(summary(regfit.fwd)$adjr2) #输出调整后R2准则下的最优模型预测变量个数
points(15, summary(regfit.fwd)$adjr2[15], col = "red", cex = 2, pch = 20) #在图中标出最优模型预测变量个数
plot(summary(regfit.fwd)$cp, xlab = "Number of Variables", ylab = "Cp", type = "l") #画出Cp与变量个数的关系图
which.min(summary(regfit.fwd)$cp) #输出Cp准则下的最优模型预测变量个数
points(14, summary(regfit.fwd)$cp[14], col = "red", cex = 2, pch = 20) #在图中标出最优模型预测变量个数
which.min(summary(regfit.fwd)$bic) #输出BIC准则下的最优模型预测变量个数
plot(summary(regfit.fwd)$bic, xlab = "Number of Variables", ylab = "BIC", type = "l") #画出BIC与变量个数的关系图
points(13, summary(regfit.fwd)$bic[13], col = "red", cex = 2, pch = 20) #在图中标出最优模型预测变量个数
15
14
13
从后面的三张图可以看出,预测变量个数从1增加到5这个阶段内,模型的精度提升很快,预测变量继续增加,模型精度趋于平稳。
三种准则给出的最优模型不一样,分别为15、14、13,但是从图中可以看出,没有充分的证据能说明15、14、13这三个模型的精度有差异,所以为了降低模型的复杂度,根据BIC准则,选取13个预测变量的模型。
向前逐步选择法告诉我们,13个预测变量的模型包含了"Outstate", “Private”, “Apps”, “Accept”, “Top10perc”, “F.Undergrad”, “Room.Board”, “Personal”, “PhD”, “Terminal”, “S.F.Ratio”, “perc.alumni”, “Expend”, “Grad.Rate”
coef(regfit.fwd, 13) #查看13个预测变量的线性模型的系数
newcollege = college[, c("Outstate", "Private", "Apps", "Accept", "Top10perc", "F.Undergrad",
"Room.Board", "Personal", "PhD", "Terminal", "S.F.Ratio", "perc.alumni", "Expend",
"Grad.Rate")] #将不需要的预测变量删去,获得新的数据集
-
(Intercept)
- -1892.07713634199 Private
- 2265.83016853156 Apps
- -0.283975257681937 Accept
- 0.718371544900607 Top10perc
- 22.4612567540299 F.Undergrad
- -0.168147955025797 Room.Board
- 0.888833534297277 Personal
- -0.249201636844794 PhD
- 12.8091799114049 Terminal
- 23.6504462927951 S.F.Ratio
- -46.9406094582559 perc.alumni
- 41.012859922414 Expend
- 0.198501137697485 Grad.Rate
- 23.626834893044
三、建立gam模型
college数据集共有777个观测,我们需要将它分成两个子集——训练集与测试集。
随机的从777个观测中选取259个作为测试集,其他的作为训练集。
set.seed(3) #为可重复性考虑,设定随机数种子
test = sample(777, 259) #从1-777中随机选取数据进入测试集
newcollege_train = newcollege[-test, ]
newcollege_test = newcollege[test, ]
建立广义可加模型,这其中除了分类数据Private为一阶线性的外,其他的预测变量都以自由度为3的光滑样条的形式出现在广义可加模型中。
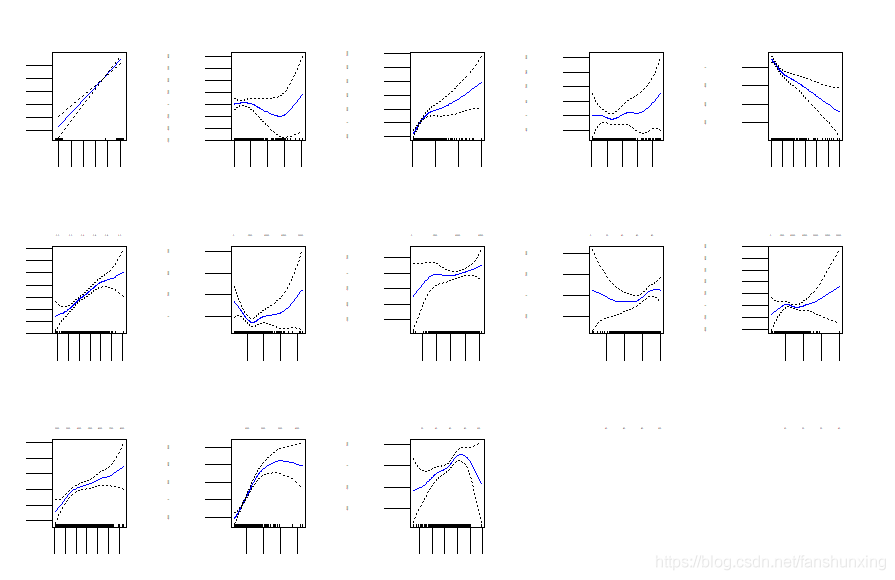
画出这13个预测变量的局部依赖图。
library(foreach)
library(splines)
library(gam)
fit1 = gam(Outstate ~ Private + s(Apps) + s(Accept) + s(Top10perc) + s(F.Undergrad) +
s(Room.Board) + s(Personal) + s(PhD) + s(Terminal) + s(S.F.Ratio) + s(perc.alumni) +
s(Expend) + s(Grad.Rate), data = newcollege_train) #建立gam模型
plot(fit1, se = TRUE, col = "blue") #画出局部依赖图(共13张)
将广义可加模型fit1作用在测试集上,看看模型的精度如何,并与简单线性模型进行对比。
preds1 = predict(fit1, newdata = newcollege_test) #把用训练集拟合得到的fit1 gam模型用来预测测试集的Outstate
sqrt(mean((newcollege_test$Outstate - preds1)^2)) #算出预测结果与训练集真值之间的标准误差MSE
fit2 = lm(Outstate ~ Private + Apps + Accept + Top10perc + F.Undergrad + Room.Board +
Personal + PhD + Terminal + S.F.Ratio + perc.alumni + Expend + Grad.Rate, data = newcollege_train) #拟合一个简单线性模型fit2用于对比
preds2 = predict(fit2, newdata = newcollege_test) #运用简单线性模型fit2来预测测试集
sqrt(mean((newcollege_test$Outstate - preds2)^2)) #算出预测结果与训练集真值之间的标准误差MSE
1892.84022849016
1990.50283312372
广义可加模型预测测试集的标准误为1892,优于简单线性模型的1990
四、题目后续问题的解答
哪些预测变量与响应变量之间存在非线性关系?
在整个college数据集上建立广义可加模型fit3,R语言的描述性函数会对广义可加模型做假设检验,原假设为预测变量与响应变量间是线性关系,备择假设为预测变量与响应变量间是非线性关系。
fit3 = gam(Outstate ~ Private + s(Apps) + s(Accept) + s(Top10perc) + s(F.Undergrad) +
s(Room.Board) + s(Personal) + s(PhD) + s(Terminal) + s(S.F.Ratio) + s(perc.alumni) +
s(Expend) + s(Grad.Rate), data = newcollege) #在整个college数据集上构建广义可加模型fit3
summary(fit3) #查看fit3的假设检验结果
Anova for Nonparametric Effects
Npar Df Npar F Pr(F)
(Intercept)
Private
s(Apps) 3 3.3509 0.018643 *
s(Accept) 3 9.1271 6.188e-06 ***
s(Top10perc) 3 0.9018 0.439859
s(F.Undergrad) 3 3.1151 0.025649 *
s(Room.Board) 3 1.5387 0.203140
s(Personal) 3 4.7410 0.002778 **
s(PhD) 3 2.6190 0.049876 *
s(Terminal) 3 1.1730 0.319081
s(S.F.Ratio) 3 5.0551 0.001799 **
s(perc.alumni) 3 1.1565 0.325496
s(Expend) 3 28.9299 < 2.2e-16 ***
s(Grad.Rate) 3 2.9458 0.032215 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
P值越小,越拒绝原假设,也就是说此时预测变量与响应变量有显著的非线性关系。
所以Apps、Accept、F.Undergrad、Personal、PhD、S.F.Ratio、Expend、Grad.Rate都与响应变量Outstate存在非线性关系。
至于Private,由于它是二元变量,没有线性不线性一说,所以它没有p值。
五、模型的优化
根据假设检验,我们知道了哪些预测变量与响应变量有显著的非线性关系,那么我们就对这些变量构建光滑样条函数,然后将其他的变量视作线性关系,再次建立广义可加模型,并评估它的精度。
fit4 = gam(Outstate ~ Private + s(Apps) + s(Accept) + Top10perc + s(F.Undergrad) +
Room.Board + s(Personal) + s(PhD) + Terminal + s(S.F.Ratio) + perc.alumni + s(Expend) +
s(Grad.Rate), data = newcollege_train) #在训练集上构建新的gam模型fit4
preds4 = predict(fit4, newdata = newcollege_test) #预测测试集
sqrt(mean((newcollege_test$Outstate - preds4)^2)) #算出标准误
Warning message in model.matrix.default(mt, mf, contrasts):
"non-list contrasts argument ignored"
1866.6052984557
改进后的广义可加模型fit4的预测集标准误为1866,比原来的广义可加模型fit1更精确。