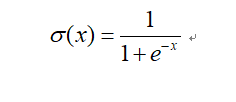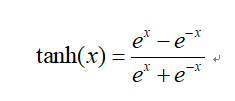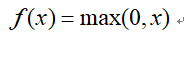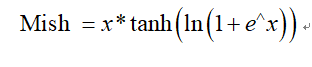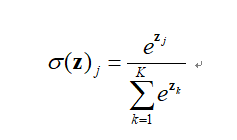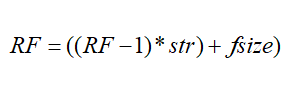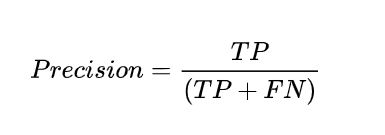【深度学习笔记】 【深度学习混淆专业名词解释】

1.监督学习、无监督学习、半监督学习和强化学习到底有什么区别？

Supervised learning（监督学习)

它是有特征（feature）和标签（label）的，即便是没有标签的，机器也是可以通过特征和标签之间的关系，判断出标签。举例子理解：高考试题是在考试前就有标准答案的，在学习和做题的过程中，可以对照答案，分析问题找出方法。在高考题没有给出答案的时候，也是可以给出正确的解决。这就是监督学习。
一句话概括：给定数据，预测标签。
通过已有的一部分输入数据与输出数据之间的对应关系，生成一个函数，将输入映射到合适的输出，例如分类。

Unsupervised learning（无监督学习)

只有特征，没有标签。举例子理解：高考前的一些模拟试卷，是没有标准答案的，也就是没有参照是对还是错，但是我们还是可以根据这些问题之间的联系将语文、数学、英语分开，这个过程就叫做聚类。在只有特征，没有标签的训练数据集中，通过数据之间的内在联系和相似性将他们分成若干类。
一句话概括：给定数据，寻找隐藏的结构。
直接对数据集建模。
以上两者的区别：监督学习只利用标记的样本集进行学习，而无监督学习只利用未标记的样本集。

Semi-Supervised learning(半监督学习)

使用的数据，一部分是标记过的，而大部分是没有标记的。和监督学习相比较，半监督学习的成本较低，但是又能达到较高的准确度。
综合利用有类标的和没有类标的数据，来生成合适的分类函数。
半监督学习出现的背景：实际问题中，通常只有少量的有标记的数据，因为对数据进行标记的代价有时很高，比如在生物学中，对某种蛋白质的结构分析或者功能鉴定，可能会花上生物学家很多年的工作，而大量的未标记的数据却很容易得到。

Reinforcement learning(强化学习)

强化学习也是使用未标记的数据，但是可以通过一些方法知道你是离正确答案越来越近还是越来越远（奖惩函数）。可以把奖惩函数看作正确答案的一个延迟、稀疏的形式。可以得到一个延迟的反馈，并且只有提示你是离答案越来越近还是越来越远。

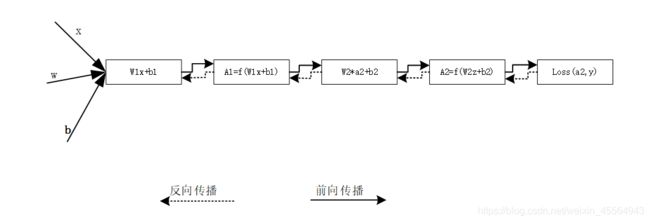
2.理解前向传播、损失函数、反向传播的概念及具体过程

2.1前向传播

前向传播算法（Forard  Propagation），它是一种将大脑神经网络的基本结构信息进行深度向前传播计算的一种方式。前向信号传播网络算法通常认为需要对进入神经网络的各种信号输入，神经网络的相互连接网络结构和各个输入神经元之间的相互作用关系进行详细描述。简单来说，其定义就是：将上一层的输出作为下一层的输入，并计算下一层的输出，一直到运算到输出层为止。

2.2损失函数

损失函数( loss function )通常是指衡量二元模型中所预测的值与真正实值之间的不一样性和复杂程度，通常被认为是二元模型中的实值非负函数，用L（θ，d）表示。在实际问题中，损失函数通常是表示真实值和预测值之间的距离。损失越小，即表示真实值和所预测值之间的偏差就越小，模型也就相应比较准确。损失函数也可以被认为是任何一个函数。然而，通常采用均方误差法和交叉熵误差法。 

2.3反向传播算法

反向传播算法，英文名称为Back Propagation（bp），它是一种高效地从所有的参数中运用梯度下降算法。在进行训练的整个过程中，前向传播的目标是因为它会产生一个损失函数，而反向传播则是因为它能够让来自这个损失函数的信息能够通过网络进行逆向流动，从而以便于计算得出梯度。逆向传播算法主要包含两个环节，分别是激励性传播和权重的更新。通过这两个环节进行反复的循环迭代，一直到整个网络的针对于输入的响应都能够达到其预定的目标区域范围。简单的说法就是，先将输出参数进行向前计算，再将其输入值进行反向传递，再通过相互之间的逆转运动来修改参数，到最后可以将损失函数输入最小时的参数修改成作为最后一次学习的参数。

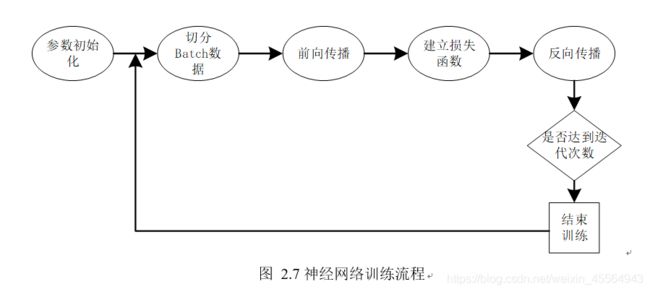
3.神经网络的训练流程是怎样的？

神经网络的训练的目的是从训练数据中地洞获得最佳权值参数的过程，分为两个阶段：

1. 通过前向传播的算法进行计算可以得到预测值，然后再进行计算出所预测值与真实估计值之间的误差大小，此误差也可以叫做损失函数。
2. 通过反向传播算法计算损失函数对于每一个参数的梯度，然后使用合适的梯度下降算法对参数进行更新。

基本流程如下：

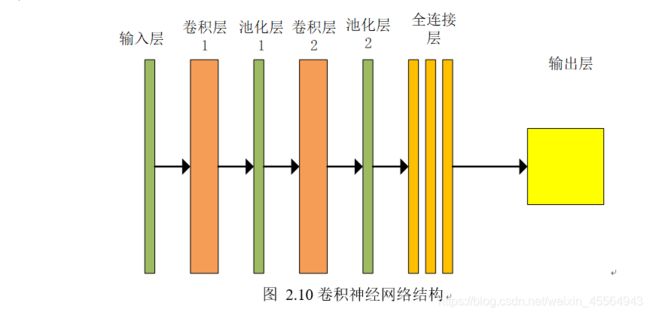
4.卷积神经网络的结构是什么？

卷积神经网络，即Convolutional Neural Network（cnn），是在我国计算机视觉及图像信号处理技术等领域比较受欢迎且应用范围广泛的一种新型神经网络。比较于全连接式神经网络，卷积式神经网络已被引入卷积层架构与池化层架构，这两层都是 cnn 重要的组成部分。比较简单的卷积式神经网络框架如下: 

2.1卷积神经网络一般由卷积层、池化层、全连接层构成。

卷积层：

卷积，即convolutional，它是特别用来替代一般矩阵的线性运算，其目的是提取图像特征。具体来说，针对一个大型图像的像素灰度为一个像素矩阵，卷积的一个工作基本原理也就是我们只要利用一个卷积软件内核可以进行逐步地计算扫描一个新的像素矩阵，然后与一个新的像素灰度矩阵里的每一个灰度元素矩阵进行相乘运算即可从而得到一个新的图像灰度为一个像素矩阵，整个扫描过程也就是卷积。通常卷积大致可以分为三种卷积形式：full卷积、same卷积和函数valid卷积。其卷积运算由两个关键的参数来定义：

1. 卷积核大小：一般为3 * 3 或者5 * 5 。
2. 输出特征图的深度：一般由使用卷积核数量决定。

池化层：

池化运算的操作，即 pooling ，其主要功能之一就是对卷积的结果做进一步的处理，对卷积的基本特征也做进一步的处理。具体来说，它主要是将一个平面内的某一个位置和其相邻的特征数据进行了统计和汇总，然后把统计和汇总的结果当做是此位置在此平面内的数据输出，其操作又有点类似于传统的图像处理中的减少样本数目量的操作。一般可以划分为 same 池化和 valid 池化，按照功能详细分配的话，可以划分为平均值池化和最大价值池化。

2.2卷积层和池化层的区别： 

对比于卷积和池化，他们有如下两方面主要的区别：

1. 卷积核的权重我们可能需要确认已经被设定,或者在进行计算的过程中经由机器学习的算法来自动进行优化后才能够得出，它可以是一个完全未知的参数；而且池化并非没有任何未知的参数所需要进行估计，同时也不会出现任何参数被优化的操作过程，因此于对计算机而言，池化操作就是非常简易。
2. 对于一个矩阵输入的任意通道的所有像素矩阵，只要它们都可以是卷积计算，一个卷积计算核的分层计算只有一个机会在其中直接产生一个输入通道；但是于矩阵池化而言，它实际上也只是一种基于矩阵分层化的运算，所以矩阵输出的通道像素每个矩阵输入通道的卷积大小主要取决于每个矩阵输入中的像素以及每个矩阵的输出通道的数量。

5.数据增强的概念是什么？它有什么作用？

 5.1数据增强概念

 数据增强，即Data Augmentation，它通过对数据施加各种变换来达到增加样本量的目的。

一般而言，对于数据增强可以分为两类：离线增强和在线增强。

1. 离线增强 ：直接对一个数据集中的因素进行处理，数据个数就转化为了增强因素乘以其中的原始数据集。此种方法通常适合在数据集规模较小的场景中使用。
2. 在线增强 ：这种增强方法是用来获取批处理数据，然后对批处理数据进行增强，如旋转、平移、折叠等相应的变化，由于一些数据集不能接受线性水平增长，这种方法长期用于大数据集，许多机器学习框架已经支持这种数据增强方法，并可以使用gpu来优化计算。

5.2数据增强作用：

数据增强作用：

简单地说就是为了让有限度的数据生成和产生更多的信息，具体地说就是通过增加训练样品(包括噪声和信息)的数量和多样性，以及改善和提高模型的鲁棒性，即通过设计的目标检测模型能够比从不同的环境中所获得的图像更加具备鲁棒性。神经网络在工作时需要很多参数，其中很多有数百万个参数，要使这些参数正确工作需要大量的数据进行训练，但在很多实际项目当中，我们很难找到足够的数据来完成任务。随机改变训练样本可以减少模型对某些属性的依赖，从而提高模型的泛化能力。

6.激活函数是什么？各有什么优缺点？

6.1概念

激活函数在物理学上是人体和机械学中的一个重要组成部分，它的本质就是一个非线性的信号，通过接收一个真正的实数来作为信号的输入然后再产生一个真正的实数输出，其主要功能就是通过这种方式来增加人体与神经网络之间的一种信号表达能力，从而促进其对复杂的非线性信号进行处理。目前比较常用的激活函数有sigmoaid，tanh，relu,mish等。

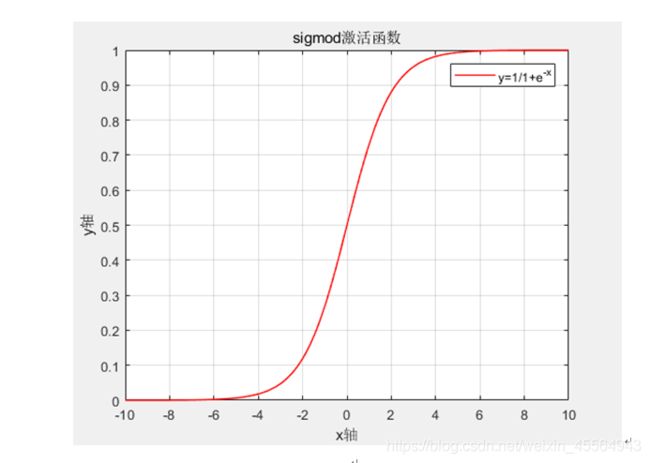
 6.2 sigmoid函数

sigmoid函数：它是接收一个输入的实数，并且可以使其在输出中的映射行为[0,1]之间的数，表达式和图像如下。

                                                      

图像如下所示：

其优缺点如下：

优点：

1.输出范围有限，优化稳定，可以作为输出层。

2.连续函数，便于求导。

缺点：

1. 当变量绝对值取值较大时会出现饱和现象，意味着函数变得很平，对微小的输入变化不明显。比如在反向传播时，当梯度接近零时，权重基本上就不会有更新，就可能会比较轻松地出现权重和梯度的消失这种情况，后续就可能无法很好地完成对于深层次网络的培训。
2. 由于函数时指数形式，所以复杂度比较高。
3. sigmoid函数一旦输出并不是零均值，可能就会在某种情况下导致一个神经元在输入为非零均值的信号时会直接对其梯度造成影响。

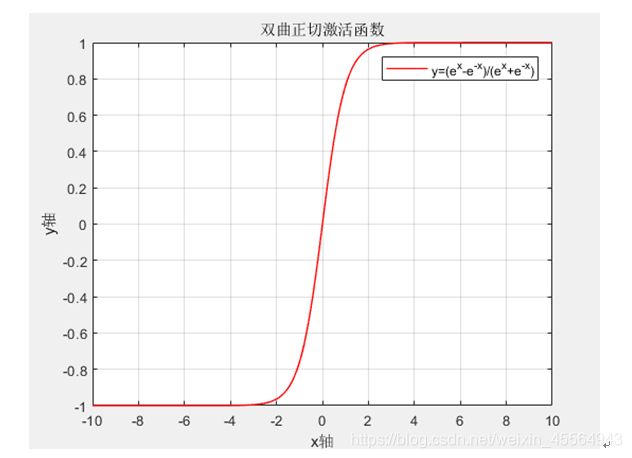
6.3 tanh函数

接收一个映射实数，并将其在这个表达式中输出一个值为[-1,1]可见的一个映射函数，表达式如下：

                                                      

其优缺点如下：

优点：与 sigmoid 函数相对于零点进行比较，它的一个输出平方均值为零，图像关于零点对称，其收敛的速度远远要比 sigmoid 快，从而大大减少了迭代的次数。

缺点：与tanh函数一样具有软饱和性的性质，会造成梯度消失的现象，从而两边会有趋近零的情况，就会存在梯度消失和幂运算的问题。

6.4 relu函数

                                                                 

其优缺点如下：

优点：

1. 梯度不饱和，收敛的速度比较快。
2. 比较于sigmoid/tanh激活函数，这个激活函数很好地改善了梯度变换消失的问题。
3. 不需要进行指数运算，所以具有运算速度快、复杂度低的优点。

   缺点：

1. 对参数的初始化和学习率非常之敏感，有神经元死亡现象。
2. Relu函数所有的输出均也大于零，网络的运动收敛性主要受到运动偏移反射现象和运动神经元细胞死亡的共同相互作用力的影响。

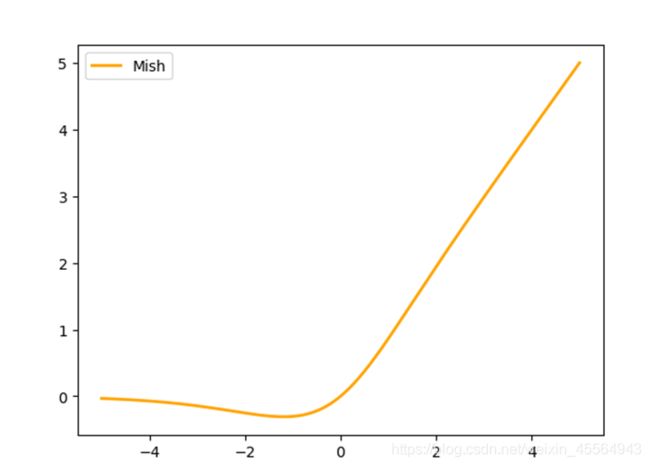
6.5 Mish函数

具有低代价成本，平滑、非单调、上无界和有下界等特点，与其它常用函数，例如Relu、swish等函数相比，提高了它的可靠度和性能。提高了它的性能。本篇下文讲述的yolov4就是用的此激活函数，表达式如下：

                                            

7.softmax是什么？

在真正的深度学习视频图像处理技术的应用中，分类这样的问题已经十分普遍，甚至需要相当于连续型变量。分类问题可以说已经成为了机器学习技术领域当中的基础性问题之一，例如，对于图像识别、字符识别、语音识别等方面的问题均可以将其转化成基本的分类问题。逻辑概率回归( logistic regression )，又称逻辑对数概率回归，是研究机器学习技术领域的最具经典性的分类仪。然而，它仅仅只能被应用于简单的二值划分问题。 Softmax 分类器主要是对于逻辑性回归的一种推广，它是一种能够同时解决多个分类问题的模拟式分类器。这类多类线性分类器可以通过分类器的输出得到每个类别的近似概率预测，从而处理多分类问题。在多种类型的机器学习和深度学习中有着广泛的应用。Softmax回归的数学表达式如下：

                                                    

其中，Softmax函数具有以下两个重要性质：

1. 函数输出总是0~1的实数。
2. 函数的输出和是1。

其中第二条特征是性质的输出与为1，这是 Softmax 的一个重要特点，正因如此 Softmax 的输出才可以被解释为"概率"。同时，对于一个 n 分类的问题，输出层神经元的个数一般也就是每一个类别的个数，此函数计算每一个神经元映射到相应类别的概率，然后以输出值最大的神经元所需要映射到的类别为最后一个目标识别的输出。

8.过拟合、欠拟合、正常拟合概念

过拟合：指在模型训练的过程中，模型对于训练数据造成过度的现象，从而将训练数据中包含的各种噪声和误差也进行了学习，从而使得模型在一些训练集上表现出“很好”的现象，而在测试集上表现出“很差”的现象。

欠拟合：指由于自己的模型过于简单而出现难以学习训练数据的规律而出现的在训练数据集上表现很差的现象。

正常拟合：指自己的模型合理地学习了训练数据集的规律，没有过多关注噪声部分，使得模型在测试数据上具有很好的表现效果。

9.什么是BN？

BN，即Batch Normalization，,是一种对数据进行归一化计算方法，其往往被广泛应用于深度学习神经网络激活函数前，其主要功能作用时可以加快对模型训练的收敛率和运动速度，使得该模型在进行训练的过程中更加稳定，从而有效地避免了模型发生梯度爆炸和其他梯度消失等现象，并且在一定的程度上有效地起到正则性变量作用，以防止过拟合现象，这个在一定程度上几乎代替了Dropout的作用[35]。BN有以下四方面的优势：

(1) 初始训练可以选择更大的机会和初始学习频率，让人员的训练效果得到提升。以前在对网络进行训练达到一半时候，还会急切地让学习率得到调小，现在我们虽然可以考虑采用初始更大的方式来学习，但是由于学习率衰减的速度也很快，因为这种算法的收敛很快。同时即便这个算法虽然选取了必较小的学习频率，但是也比以前的收敛速度快很多，因为其特点就是能够通过快速的训练来收敛。

(2)其次我们可以不用关心在过拟合中Dropout、L2和L1正则项参数的选择问题，应用这个BN正则算法就可以简单地直接移除所有这两项的正则参数，或者我们现在就可以简单直接地选择更小的一个L2正则或者更大L1正则所符合要求的一个约束正则参数了，因为应用BN算法的一个基本技术特性就是它们已经具有较大幅度提升了针对网络信息泛化的计算能力。

(3)然后我们也不需要使用局部响应归一化层（局部响应归一化是Alexnet网络[36]用到的一种基础方法），因为BN算法实际上本身就是一个归一化的网络层。

(4) 同时最后也是我们可以把所有训练的数据完全打乱，这样做的主要目的就是为了防止在进行每批训练的过程中，某一个样本都会经常被我们挑选得到，从而出现过拟合现象。

10.非极大抑制（NMS）具体是什么？

非极大抑制算法，即Non-Maximum Suppression，简称NMS。这是一种常用的对于bound ing box（边界框）进行筛选的方法。从简单方面上来说，即通过筛选得到一定范围内所有属于相同种类的得分值最大的模型框。非极限性抑制具体实现方式如下:

1. 对所有图片进行循环。
2. 找出所有图片对应的框当中得分值大于门限函数的框。然后进行得分的筛选，从而可以极大幅度的减少框对应的数量。
3. 通过判断第二步骤所得到的框数量与得分方法。所得到的预测结果中框位置可以和其他方法相同地堆叠。此时最后一个维度里面的所有内容都由“5+num_ classes”改为了“4+1+2”，这四个参数“4”分别代表框的大小和位置，一个参数代表“1”来检查预测框中是否有其他物体，两个参数“2”分别代表了被划分的物体置信程度与其他种类的概率。
4. 通过对种类进行循环处理，非极大幅度抑制当中的筛选一定范围内的属于相同种类中得分最高的框的功能，对各种类型进行一次循环处理,它能够有效地帮助我们针对各个类型分别做出非极大的抑制。
5. 根据所得分数对该种类进行从大到小的排序。
6. 通过每次取出得分值最大的框，然后计算出它与其它所有预测框的重合程度，然后将针对重合程度过大的框除去。

11.感受野是什么？

感受野，即Receptive Field，简称RF，表示卷积神经网络当中的每一层输出的特征图像素点映射到原始图像上的范围大小。简单的来说，就是图像输出的每一个特征（即每一个像素）到底是受原始图像上的哪一区域的影响。基本公式如下：

                                           

其中，str表示卷积步长，fsize则表示卷积层滤波器的大小。   

12.模型训练过程中batch、epoch、teration概念分别指什么？

batch：我们在进行模型的训练时,需要通过使用一个训练集当中的一小部分样本的数据来对模型的权重和值进行一次反向传递的参数更新，而这一小部分的样本就被我们统统地命名为"一批数据"，即 batch，而这批数据的最大数量就是batch_size。或者简单来说，在深度学习中，当采用任意梯度训练算法进行训练时，即每次训练在训练集中取batch_size个样本训练。

在训练过程中我们需要不断适当地调整batch_size的大小，如果太小会造成训练过程时间花费过多，同时会产生梯度震荡严重的现象，不利于收敛；如果过大，不同batch的梯度会在方向上没有任何变化，而且容易陷入局部极小值，同时对于GPU的内存消耗也会过大

epoch：我们在使用训练集的全部数据对模型进行一次完整训练，也被称之为“一代训练”。简单来说1个epoch就相当于使用训练集中的全部样本训练一次的过程，通俗的讲epoch的值就是整个数据集被全部训练的代数（或者叫做次数）。

Iteration：这个表示在使用一个 batch 数据对训练模型进行一次完整参数更新的过程，同时也被称之为“一次训练”。

13.目标检测中的先验眶（Anchor）指什么？

13.1 bounding box regression

如图所示，图中的狗子是我们要检测的目标，也即是红框(Ground Truth)圈住的物体。在通常情况下模型预测到的框是绿色框。但是由于绿色框不准，相当于没有正确的检测出狗子。所以我们希望有一个方法对绿色框进行调整，使得绿色框更接近红色框。

对于预测框我们一般使用（ x , y , w , h ） （x,y,w,h）（x,y,w,h）来表示，其中x , y x, yx,y代表预测框的中心点，w , h w,hw,h代表预测框的宽高。

现在设红框的坐标信息为：
G = [ G x , G y , G w , G h ] G = [G_x,G_y,G_w,G_h]
G=[Gx ,Gy,Gw ,Gh ]

绿框的坐标信息为：
G ′ = [ G x ′ , G y ′ , G w ′ , G h ′ ] G' = [G'_x,G'_y,G'_w,G'_h]
G ′ =[Gx′ ,Gy′ ,Gw′ ,Gh′ ]

那么要经过怎么样的调整才能使得绿框变成红框呢？目标检测中的做法是：平移+缩放。

将预测框的中心点平移到与真实框的中心重合的位置。
再将预测框的高和宽缩小或放大到与真实框一样的长度。
众所周知，平移至重合位置需要两个偏移量 ，缩放也需要两个系数

那么显然这个偏移量与缩放系数的大小与真实框实际的偏差有很大关联。若原本预测框与真实框就很接近，需要偏移和缩放的大小也就少一点，反之亦然。所以我们肯定希望预测框与真实框越接近越好。

但是真实的情况往往是不同的，数据中的真实框都是各种各样的，有的可能非常大，有的可能非常偏，数据分布非常不统一，而预测框就更不用说了。这就导致了学习到的偏移量和缩放系数变化大，模型难收敛的问题。所以为了解决这个问题，我们引入了Anchor机制。

13.2 Anchor

虽然我们不能约束预测框的位置，但是可以统一真实框的位置。我们将假设我们将所有真实框的长宽都设为128，把这个长宽都为128的框叫做先验框(Anchor)，也就是图中蓝色的框。那么这样模型学习到的系数都会偏向这个先验框。那么有人就会问了，那这个预测框要如何转为真实框？很简单，也是将它进行平移+变换的操作变回真实框。

而加入了多个尺度之后，真实框如何选择合适的anchor又成了一个问题。一般我们选择IOU最大的作为先验框。

而这种固定尺度的anchor也会有缺陷，不能很好的适应所有数据集。例如coco数据集中就有很多小目标。所以后面也有YOLOv3这一类的目标检测模型使用k-means算法对所有真实框进行筛选。选出最有代表性的几个尺度作为anchor。
 

13.3 在什么阶段进行先验框匹配？

一般来说，我们都会在经过骨干网络处理的特征层上进行先验框匹配。因为如果在一开始的图片上就进行先验框匹配，那就会有很多先验框，这样计算量就会激增。

14.什么是AP、MAP、TP、FP、TN?

涉及概念：

平均精度（AP：Average Precision）、平均精度均值（mAP：Mean Average Precision）、查准率（precision）、查全率（recall），IOU（Intersection over Union）、置信度阈值（confidence thresholds）
 

查准率（precision）和查全率（recall，召回率）：
对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为

真正例（true positive）：预测为1，实际也为1

假正例（false positive）：预测为1，实际也为0

真反例（true negative）：预测为0，实际也为0

假反例（false negative）：预测为0，实际也为1

四种情形，令TP（真正例）、FP（假正例）、TN（真反例）、FN（假反例）分别表示其对应的样例数，则显然有TP+FP+TN+FN=样例总数。

查准率P和查全率R分别定义为：

                            

                         

实际上（单类别）：预测为反例0则不框

查准率Precision为所有预测为1中正确预测的比例，也就是框对的/所有预测框数目；

查全率Recall为所有真实框中被成功预测出1的比例，也就是框对的/所有真框数目

一个例子为：P=“挑出来的西瓜中有多少比例是好瓜”，R=“所有好瓜中有多少比例被挑出来”。

查全率和查准率是一对矛盾的度量。一般来说查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

15.什么是IOU？怎么表示？

其全称为Intersection-Over-Union，即交并比。计算预测框和标注框(即GT框)的交并比，就可以知道它们的“贴合程度”好不好，作为调整模型的指导。 

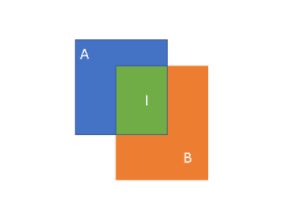
用图形表示为：

                                                     

IOU = 绿色面积/(蓝色面积+绿色面积+橙色面积) ，所以肯定是这个值越大越好。

而IOU loss可以简单表示为： 

而后边还有推广，比如CIOU、GIOU、DIOU等，对于它们的解释可以在以下链接中详细了解：

https://muzhan.blog.csdn.net/article/details/114655338 

16.什么叫Region Proposal Network(RPN)？

这个在中文里边叫做候选区域，在Faster-RCNN网络架构中直接使用 RPN 生成检测框，能极大提升检测框的生成速度。

关于这个问题的详细讲解和介绍，我这里有一个博主写的非常好，这里把链接推给大家：

https://zhuanlan.zhihu.com/p/106192020

17.什么叫label smoothing（标签平滑）？起的主要作用是什么？

对于一个神经网络，它会促使自身往正确标签和错误标签差值最大的方向学习，在训练数据较少，不足以表征所有的样本特征的情况下，会导致网络过拟合。

为解决这个问题，我们引入了label smoothing（标签平滑）

label smoothing可以解决上述问题，这是一种正则化策略，主要是通过soft one-hot来加入噪声，减少了真实样本标签的类别在计算损失函数时的权重，最终起到抑制过拟合的效果。 

例如在TensorFlow中增加label smothing（标签平滑）的实例如下：

def smoothing_cross_entropy(logits,labels,vocab_size,confidence):
  with tf.name_scope("smoothing_cross_entropy", values=[logits, labels]):
    # Low confidence is given to all non-true labels, uniformly.
    low_confidence = (1.0 - confidence) / to_float(vocab_size - 1)

    # Normalizing constant is the best cross-entropy value with soft targets.
    # We subtract it just for readability, makes no difference on learning.
    normalizing = -(
        confidence * tf.log(confidence) + to_float(vocab_size - 1) *
        low_confidence * tf.log(low_confidence + 1e-20))

    soft_targets = tf.one_hot(
          tf.cast(labels, tf.int32),
          depth=vocab_size,
          on_value=confidence,
          off_value=low_confidence)
    xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(
        logits=logits, labels=soft_targets)
    return xentropy - normalizing

本人学识浅薄，若有不正确的地方还望批评指正，谢谢！

后续自己也会不断更新和增补。