蓝桥杯python组一个星期备战记录贴

蓝桥杯python组一个星期备赛记录贴

前言

目前是2021年4月11日，一位python的fish准备备战一个星期后的蓝桥杯python组。之后将会做一些数据结构之类的整理。这是我第一次写博客。

我前期是刷了一点蓝桥杯官方的OJ，然后在CSDN上面看大佬的解答，然而做的都是一些非常基础简单的题目。这对于比赛显然是不够的。这里建议去找其他OJ，因为蓝桥杯的OJ并没有解答。
力扣OJ

注意事项：

一、贪心算法

认为能够通过局部最优解达到全局最优解
一般用来解决一维问题

例题一、柠檬水找零

	问题描述：在柠檬水摊上，每一杯柠檬水的售价为 5 美元。

顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：

输入：[5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。
示例 2：

输入：[5,5,10]
输出：true
示例 3：

输入：[10,10]
输出：false
示例 4：

输入：[5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。
 

提示：

0 <= bills.length <= 10000
bills[i] 不是 5 就是 10 或是 20 

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        dic = {
     5: 0, 10: 0, 20: 0}
        for bill in bills:
            dic[bill] += 1
            if bill - 5 == 15: 
                if dic[10] >= 1:
                    dic[5] -= 1
                    dic[10] -= 1
                else:
                    dic[5] -= 3
            elif bill - 5 == 5:
                dic[5] -= 1
            else:
                continue
            if dic[5] < 0:
                return False
            else:
                reture

**例题二 IPO** 
		假设 力扣（LeetCode）即将开始其 IPO。为了以更高的价格将股票卖给风险投资公司，力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限，它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。

给定若干个项目。对于每个项目 i，它都有一个纯利润 Pi，并且需要最小的资本 Ci 来启动相应的项目。最初，你有 W 资本。当你完成一个项目时，你将获得纯利润，且利润将被添加到你的总资本中。

总而言之，从给定项目中选择最多 k 个不同项目的列表，以最大化最终资本，并输出最终可获得的最多资本。

必要知识：堆模块

                    模块heapq中一些重要的函数
                                                           函 数                                                           描 述
                                                  heappush(heap, x)                                        将x压入堆中
                                                    heappop(heap)                                      从堆中弹出最小的元素
                                                    heapify(heap)                                           让列表具备堆特征
                                              heapreplace(heap, x)                            弹出最小的元素，并将x压入堆中
                                                  nlargest(n, iter)                                       返回iter中n个最大的元素
                                                    nsmallest(n, iter)                                   返回iter中n个最小的元素

————————————————

sorted()函数：
使用python对列表（list）进行排序
python3排序 sorted(key=lambda)
key=lambda 元素: 元素[字段索引]
　　例如：想对元素第二个字段排序，则
key=lambda y: y[1]

class Solution:
    def findMaximizedCapital(self, k: int, W: int, Profits: List[int], Capital: List[int]) -> int:
        if W > max(Capital): return W + sum(sorted(Profits, reverse=True)[:k])
        comb = []
        for p, c in zip(Profits, Capital):
            comb.append([p, c])
        comb.sort(key=lambda x: -x[0])
        while k:
            i = 0
            while i < len(comb) and comb[i][1] > W:
                i += 1
            if i == len(comb): break
            W += comb.pop(i)[0]
            k -= 1
        return W

二、最小生成树之Prim算法

运用了 贪心算法的基本思想，认为能够利用局部最优解而达成全局最优解。
利用两个集合来描述最小生成树的生长过程，
即：V集合和E集合
V集合用来存储点，说明我取了这个点
E用来存储边，即所取点之间的距离，该距离为一个局部最 优解。
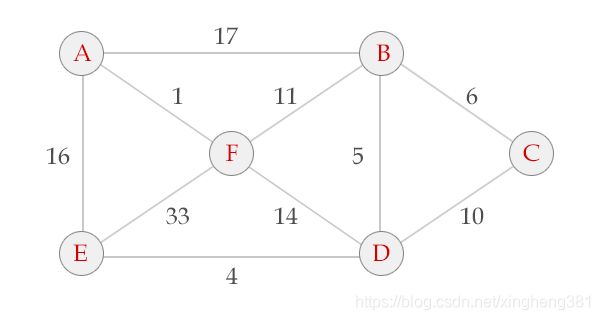
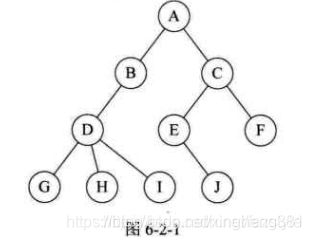
以下图为例介绍Prim算法的执行过程。

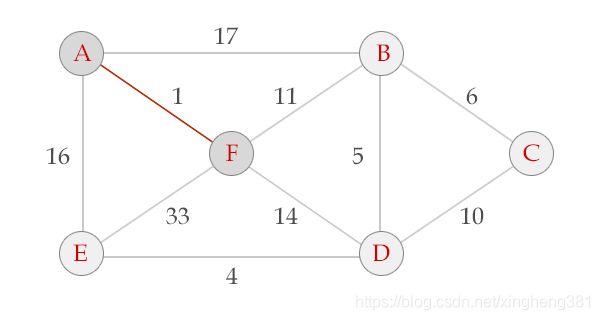
Prim算法的过程从A开始 V = {A}, E = {}

选中边AF , V = {A, F}, E = {(A,F)}

选中边FB, V = {A, F, B}, E = {(A,F), (F,B)}

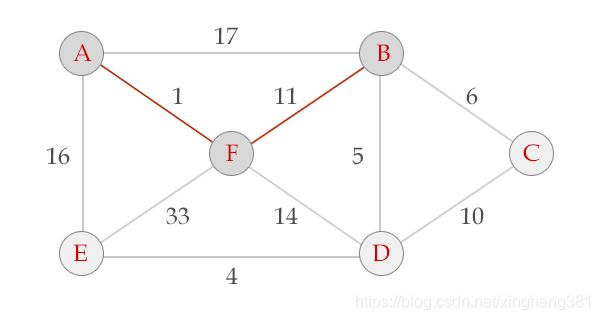
选中边BD, V = {A, B, F, D}, E = {(A,F), (F,B), (B,D)}

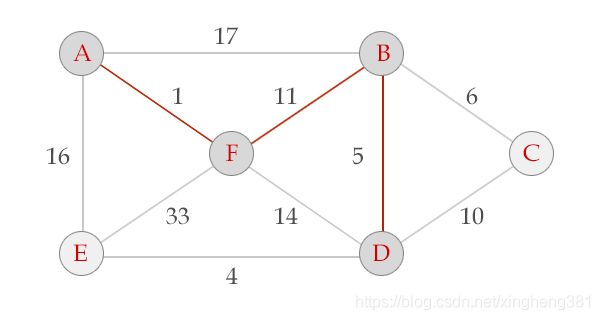
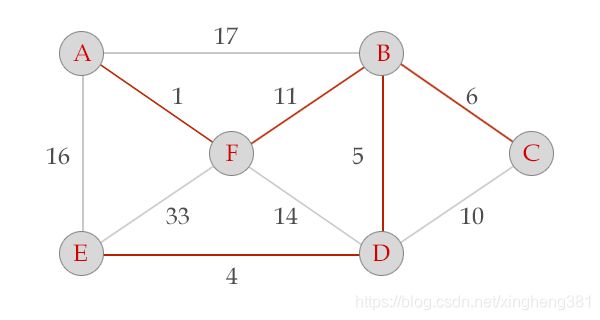
选中边DE, V = {A, B, F, D, E}, E = {(A,F), (F,B), (B,D), (D,E)}

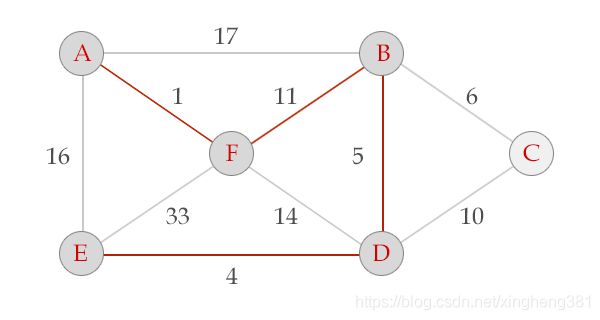
选中边BC, V = {A, B, F, D, E, c}, E = {(A,F), (F,B), (B,D), (D,E), (B,C)}, 算法结束。

三、动态规划

看了一些文章，我的理解就是打表。
在一些问题当中，如果我们使用循环来求解，可能会重复计算一个节点很多次，这就使得时间复杂度（有一说一我没学过这个概念emmmm）很大。这个时候，我们可以每计算一次，就记录下来当前的数值。这样，等到后面的时候就能直接调用。这样就能够避免重复的运算从而降低程序的时间复杂度，达到优化程序的目的。当然，有的时候表可能会很大，如果程序不要求太多的数据的话，可以保存部分的表（为啥这么多书都说的那么复杂？是我理解错了吗？感觉挺简单的，我来找几道题练练~）
例题一：买卖股票的最佳时机

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

 

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

class Solution:
    
    def maxProfit(self, prices:list) -> int:
        
        n = len(prices)
        dp = 0
        minprices = 1e9
        for i in range(n):
            if prices[i] <minprices : minprices = prices[i]
            dp = max(dp,prices[i] - minprices ) 
            
            

执行用时：
240 ms
, 在所有 Python3 提交中击败了
73.68%
的用户
内存消耗：
23.6 MB
, 在所有 Python3 提交中击败了
13.06%
的用户

注：1.我这里采用了我所谓的局部打表，就是仅仅保留了表的一个元素，按照我的理解应该会占用更加小的空间
2.我观察了一下直接用min求某个元素之前的最小值以及利用二元比较求局部最小值的方法，前者运行的时间 更长。我推测，min()、max()函数中的元素越小，程序运行时间越短
3.这里网上有的人利用了不断迭代运用min()函数求minprices，这种方法不太可取，而且经过对比，我发现在二元结构比较大小中，利用min()或max()函数运行时间要比判断结构要来的慢

ps:明明动态规划是那么简单的东西非要搞得那么复杂，利用各种修饰词来显示自己的语文很好，那些编书的人未免也太可笑了
例题二 买卖股票的最佳时期（二）

		给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

也就是说，在第一笔交易结束后才能开启第二笔交易，难点在于动态转换方程上面。

这里有个注意点，就是通过前一个转移方程控制后一个转移方程的状态。虽然是一起计算的，但是当前面一个状态转移方程没有达到最优的时候，后面的值为无效值；然而当整个程序运行完之后，这几个值就都是有效的了。
标准思路见下：
买卖股票的最佳时机（三）

这是官方的解答

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        buy1 = buy2 = -prices[0]
        sell1 = sell2 = 0
        for i in range(1, n):
            buy1 = max(buy1, -prices[i])
            sell1 = max(sell1, buy1 + prices[i])
            buy2 = max(buy2, sell1 - prices[i])
            sell2 = max(sell2, buy2 + prices[i])
        return sell2

四、递归算法

即在所定义的函数中无限套娃(这个词用得好哇有一说一，我太机智了)，从而简便计算的方法。

例题：杨辉三角取值
设 一个数在x行第y个，T(x,y)为这个数的值
则：
每行第一个和最后一个为1,T(:,0) =1,T(:,-1) = 1也可写成此时x = y
其他情况：T(x,y) = T(x-1,y-1) + T(x-1,y)

这是没采用递归时候的算法,求的是n阶的整个杨辉三角：

def triangle_yang(n):
    list1=[]
    for i in range(n):
        list1.append([1 for v in range(i+1)])
    j=1
    while j <n:
        k=1
        while k<j:
            list1[j][k]=list1[j-1][k-1]+list1[j-1][k]
            k=k+1
        j=j+1
    return list1
m=int(input())
triangle=triangle_yang(m)
for i in range(m):
    for j in range(i+1):
        print(triangle[i][j],end=' ')
    print()

这个是采用了递归之后的算法：

def getyangvalues(x,y):
    if y==0 or y==x:
        return 1
    else:
        return getyangvalues(x-1,y-1) +getyangvalues(x-1,y)


n = int(input())

for i in range(n):
    for j in range(i+1):
        print(getyangvalues(i,j) , end = ' ')
    print()

在这里，我发现采用递归的速度比没采用递归要慢。是因为这里，递归重复计算了很多项，不过在一些场合下递归要比循环快。而且代码看起来比较简洁emmmm。在这里，我因为没有学过树，所以有点对于递归的优点不是特别地理解

（象征性的）例二：求阶乘

def jiecheng(n):
    if n == 1 :return 1
    else:
        return n*jiecheng(n-1)
n = int(input())
print(jiecheng(n))

五、树与堆

树挺重要的emmm，学了这个才能学dfs和bfs算法，也才能真正理解前面的最小生成树算法。
PS：话说我还挺厉害的，今天才一周的第三天，昨天还满课来着hh，我一个非计算机系的大二学生已经学了这么多了emmm。

先来看看定义：
线性表、栈、队列、串是一对一的数据结构，而树是一对多的数据结构。
树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一棵非空树中：(1)有且仅有一个特定的称为根(Root)的结点；(2)当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、……、Tm，其中每一个集合本身又是一棵树，并且称为根的子树(SubTree)

扯那么多干啥，说白了也就两点：
(1) n = 0 时，称为空树 ；n>0时，称为非空树，且有唯一的根结点。
(2)n>1时，有子树(这玩意一看就清楚了)
(3) (我觉得这还有隐藏的一点没说)子树上面的结点不能相连，也就是说不能有环

这是错误的：

定义与专门术语的解释略

树的一些术语：

节点 （名称：键值）、边（入边、出边）、根、路径、子节点、父节点、兄弟节点、子树、叶节点、层级、高度

二叉树：每个节点最多有两个子节点

树的递归定义：树由根节点及多个子树构成的。每个子树的根到根节点都有边相连

说明：树的一些知识来源于MOOC上的北京大学陈斌老师的数据结构与算法（Python版本）
实现树：嵌套列表法
尝试利用 Python List 实现二叉树的数据结构
优点：因为子树的结构与树的结构一样，所以是一种递归的数据结构。它可以扩展到多叉树

由具有三个元素的列表实现：
第一个元素为根节点的值，第二个元素是左子树（也是第一个列表），第三个元素是右子树（也是一个列表）
例如：[ root, left, right ]（应该是树的前序遍历结构）

我们通过定义一系列的函数辅助操作嵌套列表：

BinaryTree创建仅有根节点的二叉树

insertLeft / insertRight将新节点插入树种作为其直接的左/右子节点

get/setRootVal则取得或返回根节点

getLeft/RightChild返回左/右子树

**#嵌套列表法代码**

	def BinaryTree(r):#建立根与两个空子树
		return [r , [] , []]
	def insertLeft(root,newBranch):#用newBranch代替原来所指定的节点，建立一个新树，如果原来子树存在，则作为newBranch的左子树
		t = root.pop(1)
		if len(t) > 1:
			root.insert(1 , [newBranch,t,[]])
		else:
			root.insert(1 , [newBranch, [] , [] ])
		return root
	
	def insertRight(root,newBranch):
		t = root.pop(2)
		if len(t)> 1:
			root.insert(2,[newBranch, [] , t])
		else :
			root.insert(2, [newBranch, [] , []])
		return root  
	def getRootVal(root):#返回根节点的数值
		return root[0]
		
	def setRootVal(root,newVal):#更新根节点的数值
		root[0] = newVal
	
	def getLeftChild(root):#返回左子树
	
		return root[1]
	def getRightChild(root):#返回右子树
		return root[2]
	

在这里，我偏向于边编程边学习。下面我将练习几道题还帮助我理解。

二叉树中的最大路径和：（来源：力扣（LeetCode）124）

	问题描述：
		路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
	
	 路径和 是路径中各节点值的总和。
	
	给你一个二叉树的根节点 root ，返回其 最大路径和 。

我的第一想法，是利用贪心算法的策略，意图通过局部最优达到全局最优。然而，我认为是有些问题的。接下来，我想到了递归和动态规划，列出动态转移方程求解。但当我拿到他所输入的树的时候，我又发现了一个新的问题：他的树是一个线性结构，这使得我们对它索引出现问题。于是，我去观摩了别人的代码，看看他们是怎么解决这个问题的。他们的做法非常简单，直接用 .left() 和 .right()来解决这个问题。这里有个TreeNode类