线性分类逻辑斯蒂回归多分类(11)
1.导包
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score #评估准确率得分4.0.1 加载数据
x,y=datasets.load_iris(return_X_y=True)
x_train,x_test,y_train,y_test=train_test_split(x,y,
test_size=0.2,#测试数据比例
random_state=1024)#随机打乱数据,又固定
print(x_train.shape,x_test.shape)
print(y_train.shape,y_test.shape)
输出:
(120, 4) (30, 4)
(120,) (30,)4.1 one-vs-rest
4.1.1 建模
model=LogisticRegression(multi_class='ovr')
model.fit(x_train,y_train)
y_pred=model.predict(x_test)
print(y_test[:10],y_pred[:10])
print('逻辑回归ovr实现方式的准确率:',model.score(x_test,y_test))
输出:
[1 0 2 2 0 0 1 2 1 0] [1 0 2 2 0 0 1 2 1 0]
逻辑回归ovr实现方式的准确率: 1.0accuracy_score(y_test,y_pred)#用函数算得分
输出:
1.0
4.1.2 进行概率预测
4.1.3 概率的手动计算
def sigmoid(z):
return 1/(1+np.exp(-z))
b_=model.intercept_
#方程系数
#三行:代表三个分类器(方程)
#4列,每个方程有4个系数(4个属性)
w_=model.coef_
display(w_,b_)
输出:
array([[-0.45418407, 0.77862646, -2.2268873 , -0.87662661],
[-0.41614677, -1.98168225, 0.82180991, -1.2628189 ],
[-0.28832573, -0.49869581, 2.70303022, 2.23465912]])
array([ 6.82628324, 6.16028196, -13.72510278])y_self_pred=x_test.dot(w_.T)+b_
#计算概率并归一化
p=sigmoid(y_self_pred)
p=p/p.sum(axis=1).reshape(-1,1)
print(' 手动计算的概率:',p[:3])
print(' 算法计算的概率:',proba_[:3])
输出:
手动计算的概率: [[1.53432043e-01 8.39950380e-01 6.61757687e-03]
[8.11554208e-01 1.88434331e-01 1.14614473e-05]
[1.36766700e-05 3.14582635e-01 6.85403688e-01]]
算法计算的概率: [[1.53432043e-01 8.39950380e-01 6.61757687e-03]
[8.11554208e-01 1.88434331e-01 1.14614473e-05]
[1.36766700e-05 3.14582635e-01 6.85403688e-01]]4.2.1 softmax软最大(数据--->概率)
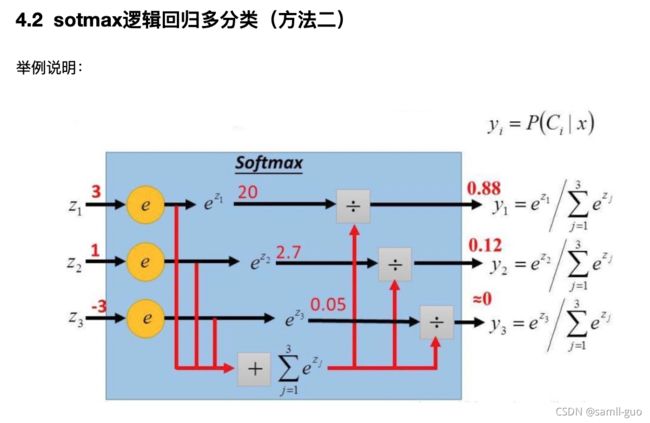
#手动计算
def softmax(z):
return np.exp(z)/np.exp(z).sum()
z=[3,1,-3]
softmax(z).round(2)
输出:
array([0.88, 0.12, 0. ])x,y=datasets.load_iris(return_X_y=True)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1024)
display(x_train.shape,x_test.shape)
display(y_train.shape,y_test.shape)
输出:
(105, 4)
(45, 4)
(105,)
(45,)4.2.2 算法概率计算
model=LogisticRegression(multi_class='multinomial')#'multinomial',进行概率多分类概率划分
model.fit(x_train,y_train)
print('算法预测准确率:',model.score(x_train,y_train))
print('算法测试数据概率准确率:\n',model.predict_proba(x_train)[:5])
输出:
算法预测准确率: 0.9714285714285714
算法测试数据概率准确率:
[[2.00300426e-03 4.55962322e-01 5.42034674e-01]
[1.66430899e-06 2.22958331e-02 9.77702503e-01]
[9.83731918e-01 1.62680180e-02 6.35758727e-08]
[1.00151318e-01 8.88996927e-01 1.08517553e-02]
[2.99509219e-04 1.80122037e-01 8.19578454e-01]]4.2.3 概率的手动计算
w_=model.coef_
b_=model.intercept_
def softmax(z):
return np.exp(z)/np.exp(z).sum(axis=1).reshape(-1,1)
z=x_test.dot(w_.T)+b_
softmax(z)[:5]
输出:
array([[1.87401166e-01, 8.07361397e-01, 5.23743739e-03],
[9.48882724e-01, 5.11164105e-02, 8.65698064e-07],
[2.00846952e-07, 6.92657016e-03, 9.93073229e-01],
[5.98531344e-04, 1.80089863e-01, 8.19311606e-01],
[9.69544607e-01, 3.04551309e-02, 2.62314352e-07]])