聚类系列算法进阶（二）19

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans,DBSCAN#导入两个聚类计算方法
from sklearn import datasets

1  创建数据

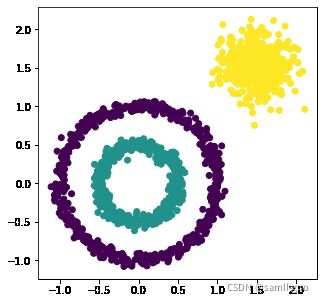
X,y=datasets.make_circles(n_samples=1000,noise=0.05,factor=0.5)
#创建环形数据，参数n_samples表示数量，noise表示数量，factor为两个圆圈的比例
np.unique(y)
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],c=y)

#生成一类点数据
X1,y1=datasets.make_blobs(n_samples=500,n_features=2,centers=[(1.5,1.5)],cluster_std=0.2)
#n_features=2表示两个特征，centers=[1.5,1.5]表示中心点位置,
#cluster_std表示标准差，标准差越大波动越大
plt.figure(figsize=(5,5))
plt.scatter(X1[:,0],X1[:,1],c=y1)

#上面两组数据进行合并
X=np.concatenate([X1,X])#级联函数合并X
y=np.concatenate([y1+2,y])
#级联函数合并y,由于y1中的一个类别直接和y合并会被涵盖，所以加2，结果才会显示3个类别
display(X.shape,y.shape)
输出：
(1500, 2)
(1500,)

#用新数据绘图
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],c=y)

2  Kmeans聚类

kmeans=KMeans(n_clusters=3)#n_clusters=3分成三类
kmeans.fit(X)
y_=kmeans.predict(X)
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],c=y_,cmap='autumn')#根据y_类别，划分颜色类别

3  DBSCAN聚类效果

dbscan=DBSCAN(eps=0.1,min_samples=3)
#eps表示聚类某个点为圆心的圆半径的大小
# min_samples表示圆圈内最小密度数量
#metric表示花圈的度量标准：如欧式距离，曼哈顿，切比雪夫等
dbscan.fit(X)
y_=dbscan.labels_#labels_,得到每个样本的标签就是分类结果
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],c=y_,cmap='autumn')

np.unique(y_)#eps半径调小，y_出现-1，异常值（离群点）类别
输出：
array([-1,  0,  1,  2,  3], dtype=int64)

 3.1  过滤异常值

cond=y_!=-1#获取除异常值外数据索引
cond
输出：
array([ True, False,  True, ...,  True,  True,  True])


plt.figure(figsize=(5,5))
plt.scatter(X[cond][:,0],X[cond][:,1],c=y_[cond])

3.2  DBSCAN可以使用轮廓系数进行评分

from sklearn.metrics import silhouette_score#导入轮廓系数

silhouette_score(X,y_)#使用轮廓系数进行评分
输出：
0.1909212973696007

4  分层聚类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering#分层聚类，自底向上聚类方式
from sklearn.datasets import make_swiss_roll#导入瑞士卷数据
from mpl_toolkits.mplot3d.axes3d import Axes3D #导入绘制3D图

4.1  创建数据

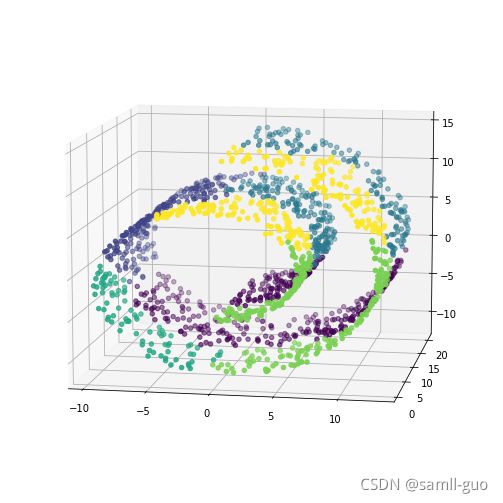
X,y = make_swiss_roll(n_samples=1500,noise = 0.05)
print(np.unique(y))
plt.figure(figsize=(12,9))
a3 = plt.subplot(111,projection = '3d')#使用3D方法

a3.scatter(X[:,0],X[:,1],X[:,2],c = y)
a3.view_init(10,-80)#调整3D角度

输出：
[ 4.71371315  4.71594512  4.71661631 ... 14.11851331 14.12255359
 14.12888384]

 

4.2  kmeans进行聚类

kmeans=KMeans(n_clusters=6)
kmeans.fit(X)
y_=kmeans.predict(X)

plt.figure(figsize=(12,9))
a3 = plt.subplot(111,projection = '3d')#使用3D方法
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)#调整3D角度

 4.3  进行分层聚类

#linkage:{'ward','complete','average','single'}
#ward 表示最小化方差
agg=AgglomerativeClustering(n_clusters=6,linkage='average')
agg.fit(X)
y_=agg.labels_

plt.figure(figsize=(12,9))
a3 = plt.subplot(111,projection = '3d')#使用3D方法
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)#调整3D角度

 

4.4  分层聚类连接性约束connectivity（空间约束）

非欧几何的数据下，可见如果没有设置连接性约束，将会忽视其数据本身的结构，强制在欧式空间下聚类，于是很容易形成了上图这种跨越流形的不同褶皱。

from sklearn.neighbors import kneighbors_graph#根据邻居远近进行分层
conn=kneighbors_graph(X,n_neighbors=10)#n_neighbors=10,采用邻居数量进行约束
agg=AgglomerativeClustering(n_clusters=6,linkage='ward',connectivity=conn)
agg.fit(X)
y_=agg.labels_

plt.figure(figsize=(12,9))
a3 = plt.subplot(111,projection = '3d')#使用3D方法
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)#调整3D角度