算法-js系列(2):动态规划-中等(1)
刷动态规划的题,感觉简单、中等的区分度没有这么高,都是能想到状态表示和状态转移方程就做的出来,想不出来就做不出来,所以重点还是在多做多想
文章目录
-
- 5_最长回文子串
- 62_不同路径
- 63_不同路径II
- 64_最小路径和
- 91_解码方法
- 96_不同的二叉搜索树
- 95_不同的二叉搜索树II
- 97_交错字符串
- 120_三角形最小路径和
- 131_分割回文串
- 139_单词拆分
- 152_乘积最大子数组
- 198_打家劫舍
- 213_打家劫舍II
- 221_最大正方形

跳过了两道别的方法的题
5_最长回文子串
5_最长回文子串
最长回文子串问题(五种方法)
// 上面的,最长公共子串方法(字符串反转后和原字符串的最长公共子串就是最长回文子串 。)是错的
// abdeba
// abedba
// 最长公共子串为 2,但最长回文子串为 1
/*
leetcode 5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
示例 3:
输入:s = "a"
输出:"a"
示例 4:
输入:s = "ac"
输出:"a"
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母(大写和 / 或小写)组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-palindromic-substring
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {string} s
* @return {string}
*/
// 动态规划
var longestPalindrome = function(s) {
// f[i] - s[0~i] 中,以第 i 个字符为结尾的回文子串的最大长度
// 状态转移 -
// f[i - 1] + 2 (s[i] === s[i - f[i-1] - 1])
// f[i - 1] + 1 (f[i - 1] === 1 && s[i] === s[i - 1]])
// ... 无法转移
// f[i][j] - s[i~j] 是不是一个回文串(i<=j)
// 状态转移
// f[i][j] = f[i+1][j-1] && s[i] == s[j]
// 初始化
// 回文串长 1:f[i][i] = true
// 回文串长 2:f[i][j] = (s[i] === s[j]) j=i+1
const n = s.length
// 定义 f 并初始化为 false
const f = new Array(n + 5).fill(0).map(() => new Array(n + 5).fill(false))
// 在状态转移方程中,我们是从长度较短的字符串向长度较长的字符串进行转移的,因此一定要注意动态规划的循环顺序。
// let res = ''
let res = [0, 0, 0]
for (let i = 0; i < n; i++) {
// i - 字符串长度-1
for (let j = 0; j + i < n; j++) {
// j - 字符串的起始位置
const k = i + j
// k - 字符串的终止位置
if (i === 0) {
// 字符串长 1
f[j][k] = true
} else if (i === 1) {
// 字符串长 2
f[j][k] = (s[j] === s[k])
} else {
// 字符串的长大于 2
f[j][k] = f[j + 1][k - 1] && (s[j] === s[k])
}
// 记录最长的回文子串
// if (f[j][k] && i + 1 > res.length) {
// res = s.slice(j, k + 1) // slice 不会影响性能,性能反而要好点
// }
// 怕 slice 影响了性能,试着只是记录最长回文子串的起止位置和长度
if (f[j][k] && i + 1 > res[2]) {
res[0] = j
res[1] = k
res[2] = k - j + 1
}
}
}
return s.slice(res[0], res[1] + 1)
}
// 中心扩展法
// 枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。
var longestPalindrome1 = function(s) {
const n = s.length
// 扩展函数
function expandAroundCenter(s, l, r) {
while (l >= 0 && r < n && s[l] === s[r]) {
l--
r++
}
return [l + 1, r - 1] // 返回回文串的左右位置
}
let start = end = 0
for (let i = 0; i < n; i++) {
// 对长度为 1 的回文串进行扩展
const [l1, r1] = expandAroundCenter(s, i, i)
// 对长度为 2 的回文串进行扩展
const [l2, r2] = expandAroundCenter(s, i, i + 1)
// 更新最长回文子串
if (r1 - l1 > end - start) {
start = l1
end = r1
}
if (r2 - l2 > end - start) {
start = l2
end = r2
}
}
// 返回最长回文子串
return s.slice(start, end + 1)
}
// Manacher 算法
// 使用臂长的概念,优化中心扩展法,跳过部分不需要比较的字符
var s = "babad"
const res = longestPalindrome(s)
console.log(res)
62_不同路径
62_不同路径-官方
62_不同路径-精选
/*
leetcode 62. 不同路径
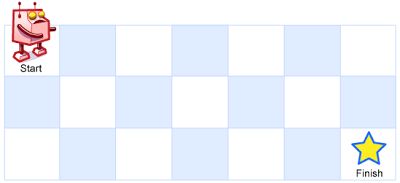
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
// 动态规划
var uniquePaths = function(m, n) {
// f(i, j) - 走到 (i, j) 共有的路径数
// 状态转移 - 最后一步是向下/右
// f(i, j) = f(i - 1, j) + f(i, j - 1)
// 将最上/左方初始化为 1(偷懒全部初始化为 1)
const f = new Array(m + 5).fill(0).map(() => new Array(n + 5).fill(1))
// 只计算第 2 行/列之后的
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
f[i][j] = f[i - 1][j] + f[i][j - 1]
}
}
return f[m-1][n-1]
};
// 动态规划 - 空间优化
// f(i, j) 仅与第 i 行和第 i-1 行的状态有关,可使用滚动数组思想降低空间复杂度
var uniquePaths1 = function(m, n) {
// m n 具有交换性,让 m 一直是较小的那个
[m, n] = [Math.min(m, n), Math.max(m, n)]
// console.log(m, n)
let pre = new Array(m + 5).fill(1)
let cur = new Array(m + 5).fill(1)
// 只计算第 2 行/列之后的
for (let i = 1; i < n; i++) {
for (let j = 1; j < m; j++) {
// j 就是遍历 m 了
cur[j] = pre[j] + cur[j - 1]
}
pre = cur
}
return pre[m-1]
};
// 动态规划 - 空间优化(进一步优化)
var uniquePaths1 = function(m, n) {
// m n 具有交换性,让 m 一直是较小的那个
[m, n] = [Math.min(m, n), Math.max(m, n)]
let cur = new Array(m + 5).fill(1)
// 只计算第 2 行/列之后的
for (let i = 1; i < n; i++) {
for (let j = 1; j < m; j++) {
// j 就是遍历 m 了
cur[j] += cur[j - 1]
}
}
return cur[m-1]
};
var m = 3, n = 7
// var m = 7, n = 3
// var m = 3, n = 2
// var m = 3, n = 3
const res = uniquePaths(m, n)
console.log(res)
63_不同路径II
63_不同路径II
/*
leetcode 63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[][]} obstacleGrid
* @return {number}
*/
// 动态规划
var uniquePathsWithObstacles = function(obstacleGrid) {
// f(i, j) - 走到 (i, j) 共有的路径数
// 状态转移 - 最后一步是向下/右
// f(i, j) = f(i - 1, j) + f(i, j - 1)
// 将最上/左方初始化为 1(不能这样初始化了,因为有障碍物后面的点不可达)
// 有障碍物处的 f(i, j) 始终为 0
const m = obstacleGrid.length
const n = obstacleGrid[0].length
// 出发点或终点有障碍物,直接返回 0——不特判也能得到正确结果
if (obstacleGrid[0][0] === 1 || obstacleGrid[m-1][n-1] === 1) {
return 0
}
// 不同的初始化方式
// const f = new Array(m).fill(0).map(() => new Array(n).fill(1))
// // 所有有障碍的地方初始化为 0
// obstacleGrid.forEach((item, i) => {
// item.forEach((x, j) => {
// if (item[j] === 1) {
// f[i][j] = 0
// }
// })
// })
// // 第 0 行中,若出现障碍物,则此后的点均初始化为 0
// for (let i = 0; i < n; i++) {
// if (obstacleGrid[0][i] === 1) {
// for (let j = i; j < n; j++) {
// f[0][j] = 0
// }
// break
// }
// }
// // 第 0 列中,若出现障碍物,则此后的点均初始化为 0
// for (let i = 0; i < m; i++) {
// if (obstacleGrid[i][0] === 1) {
// for (let j = i; j < m; j++) {
// f[j][0] = 0
// }
// break
// }
// }
// 也可以先全部初始化为 0,然后将初始可达的点置为 1
const f = new Array(m).fill(0).map(() => new Array(n).fill(0))
// 第 0 行中,若未出现障碍物,则点均初始化为 1
for (let i = 0; i < n; i++) {
if (obstacleGrid[0][i] === 1) {
break
}
f[0][i] = 1
}
// 第 0 列中,若出现障碍物,则此后的点均初始化为 0
for (let i = 0; i < m; i++) {
if (obstacleGrid[i][0] === 1) {
break
}
f[i][0] = 1
}
// 只计算第 1 行/列之后的
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
if (obstacleGrid[i][j] !== 1) {
f[i][j] = f[i - 1][j] + f[i][j - 1]
}
}
}
return f[m-1][n-1]
};
// 动态规划 - 空间优化(滚动数组思想)
// 懒得敲了
var obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
var obstacleGrid = [[0,1],[0,0]]
var obstacleGrid = [[1, 0]]
var obstacleGrid = [[0,0],[1,1],[0,0]]
const res = uniquePathsWithObstacles(obstacleGrid)
console.log(res)
64_最小路径和
64_最小路径和-官方
64_最小路径和-精选
/*
leetcode 64. 最小路径和
给定一个包含非负整数的 m * n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:

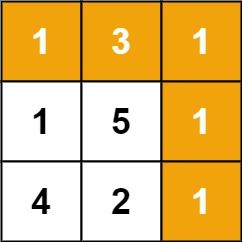
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[][]} grid
* @return {number}
*/
// 动态规划
var minPathSum = function(grid) {
// f(i, j) - 到达点 (i, j) 的路径上数字总和的最小值
// 状态转移 - 最后一步向下/右
// f(i, j) = min(f(i - 1, j), f(i, j - 1)) + grid(i, j)
const m = grid.length // [][0]
const n = grid[0].length // [0][]
const f = new Array(m).fill(0).map(() => new Array(n).fill(0))
let sum = 0
for (let i = 0; i < m; i++) {
sum += grid[i][0]
f[i][0] = sum
}
sum = 0
for (let i = 0; i < n; i++) {
sum += grid[0][i]
f[0][i] = sum
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j]
}
}
return f[m - 1][n - 1]
}
// 动态规划 - 空间优化(滚动数组)
// 空间小了 0.3MB 时间短了 4 ms
var minPathSum = function(grid) {
// f(i, j) - 到达点 (i, j) 的路径上数字总和的最小值
// 状态转移 - 最后一步向下/右
// f(i, j) = min(f(i - 1, j), f(i, j - 1)) + grid(i, j)
const m = grid.length // [][0]
const n = grid[0].length // [0][]
// [m, n] = [Math.min(m, n), Math.max(m, n)]
let cur = new Array(n).fill(0)
cur[0] = grid[0][0]
// 第一行的每列路径,全部记录下来
for (let i = 1; i < n; i++) {
cur[i] = cur[i - 1] + grid[0][i]
}
for (let i = 1; i < m; i++) {
// 第一列的每行累加
cur[0] += grid[i][0]
for (let j = 1; j < n; j++) {
cur[j] = Math.min(cur[j], cur[j - 1]) + grid[i][j]
}
}
return cur[n - 1]
}
var grid = [[1,3,1],[1,5,1],[4,2,1]] // 7
grid = [[1,2,3],[4,5,6]] // 12
const res = minPathSum(grid)
console.log(res)
91_解码方法
91_解码方法-民间
/*
leetcode 91. 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> 1
'B' -> 2
...
'Z' -> 26
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"111" 可以将 "1" 中的每个 "1" 映射为 "A" ,从而得到 "AAA" ,或者可以将 "11" 和 "1"(分别为 "K" 和 "A" )映射为 "KA" 。注意,"06" 不能映射为 "F" ,因为 "6" 和 "06" 不同。
给你一个只含数字的 非空 字符串 num ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
示例 2:
输入:s = "226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
示例 3:
输入:s = "0"
输出:0
解释:没有字符映射到以 0 开头的数字。含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。由于没有字符,因此没有有效的方法对此进行解码,因为所有数字都需要映射。
示例 4:
输入:s = "06"
输出:0
解释:"06" 不能映射到 "F" ,因为字符串开头的 0 无法指向一个有效的字符。
提示:
1 <= s.length <= 100
s 只包含数字,并且可能包含前导零。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/decode-ways
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {string} s
* @return {number}
*/
// 动态规划
var numDecodings = function(s) {
// f(i) - 以 s[i] 结尾的字符串,的解码总数
// 状态转移 - 最后一步,解码一/两个字符
if (s[0] == 0) {
return 0
}
const len = s.length
const f = new Array(len + 1).fill(0)
f[0] = 1
f[1] = 1
for (let i = 2; i <= len; i++) {
if (s[i - 1] != 0) {
f[i] = f[i - 1]
}
let num = s.slice(i - 2, i)
num = parseInt(num)
// console.log(num)
if (num >= 10 && num <= 26) {
f[i] += f[i - 2]
}
}
return f[len]
}
// 动态规划 - 空间优化(滚动数组)
// 空间减小了 0.1MB 时间增加了 20 ms
var numDecodings = function(s) {
// f(i) - 以 s[i] 结尾的字符串,的解码总数
// 状态转移 - 最后一步,解码一/两个字符
// f(i) = f(i - 1) + f(i - 2)
// 条件:s[i] != 0, s[i-1, i] 在 [10, 26] 之间
if (s[0] == 0) {
return 0
}
const len = s.length
let pre = 1
let cur = 1
for (let i = 2; i <= len; i++) {
let tmp = 0
if (s[i - 1] != 0) {
tmp = cur
}
let num = s.slice(i - 2, i)
num = parseInt(num)
// console.log(num)
if (num >= 10 && num <= 26) {
tmp += pre
}
pre = cur
cur = tmp
}
return cur
}
var s = "06" // 0
var s = "12" // 2
var s = "226" // 3
const res = numDecodings(s)
console.log(res)
96_不同的二叉搜索树
96_不同的二叉搜索树-官方
/*
leetcode 96. 不同的二叉搜索树
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-binary-search-trees
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number} n
* @return {number}
*/
// 动态规划
var numTrees = function(n) {
// G(n) - 序列长度为 n 的二叉搜索树的种数
// f(i, n) - 以 i 为根结点,序列长度为 n 的二叉搜索树的种数
// 状态转移 - 不同根结点构成所有二叉搜索树
// G(n) = f(1, n) + f(2, n) + ... + f(n, n)
// f(i, n) = G(i - 1)G(n - i) =>
// G(n) = G(0)G(n-1) + G(1)G(n-2) + ... + G(n-1)G(0)
// let g = [] // 必须初始化为 0,这样声明,里面的值是 undefined,无法计算
// console.log(g[0]) // undefined
let g = new Array(n + 1).fill(0)
g[0] = 1
g[1] = 1
for (let i = 2; i <= n; i++) {
for (let j = 1; j <= i; j++) {
g[i] += g[j - 1] * g[i - j]
}
}
return g[n]
}
// G(n) = G(0)G(n-1) + G(1)G(n-2) + ... + G(n-1)G(0) —— 卡塔兰数 C_n
// C0 = 1,C_(n+1)=2(2n+1)/(n+2) C_n
var n = 10
const res = numTrees(n)
console.log(res)
推导出来的 G(n) 的公式 G ( n ) = ∑ i = 1 n F ( i , n ) , G ( 0 ) = 1 , G ( 1 ) = 1 G(n) = \sum_{i=1}^{n}F(i, n),G(0)=1, G(1)=1 G(n)=∑i=1nF(i,n),G(0)=1,G(1)=1
上述即为 卡塔兰数 G n + 1 = 2 ( 2 n + 1 ) n + 2 C n , C 0 = 1 G_{n+1} = \frac{2(2n+1)}{n+2} C_n,C_0=1 Gn+1=n+22(2n+1)Cn,C0=1
95_不同的二叉搜索树II
这题也不是动态规划呀,先搁着,以后写递归的时候再回头来看(搁置??)
/*
leetcode 95. 不同的二叉搜索树 II
给定一个整数 n,生成所有由 1 ... n 为节点所组成的 二叉搜索树 。
示例:
输入:3
输出:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
提示:
0 <= n <= 8
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-binary-search-trees-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number} n
* @return {TreeNode[]}
*/
var generateTrees = function(n) {
};
97_交错字符串
97_交错字符串-官方
「手画图解」DFS 回溯 及其优化
这个 DFS 回溯讲的很清晰,到时候做 DFS 回溯板块的时候,要回来看
/*
leetcode 97. 交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
提示:a + b 意味着字符串 a 和 b 连接。
示例 1:

输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出:false
示例 3:
输入:s1 = "", s2 = "", s3 = ""
输出:true
提示:
0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/interleaving-string
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {string} s1
* @param {string} s2
* @param {string} s3
* @return {boolean}
*/
// 动态规划
var isInterleave = function(s1, s2, s3) {
// 能决定下一步的是?现在选择的是哪个字符串,另一个字符串从哪里选择
// f(i, j) - s3[i~] 是从 j(0/1) 字符串选择的
// 放弃
// 上面的思路错了——不用管交错的,直接一个字符一个字符接着匹配就行
// 主要是看 s3 的字符能不能和 s1/s2 的字符匹配
// f(i, j) - s1[1~i] 和 s2[1~j] 能否交错组成 s3[1~i+j]
// 状态转移 - s3[i+j] 最后是和谁匹配的 s1[i] 还是 s2[j]
// (f(i - 1, j) && s1[i] === s3[i + j]) || (f(i, j - 1) && s2[j] === s3[i + j])
const len1 = s1.length
const len2 = s2.length
if (len1 + len2 !== s3.length) {
return false
}
const f = new Array(len1 + 5).fill(false).map(() => new Array(len2 + 5).fill(false))
// f[0, x] f[x, 0] 都要初始化出来 f[0, 0]-用不到,可以不管
f[0][0] = true // 如果传入的都是空串,就要初始化 f[0, 0]
// 初始化复杂了 - 动态转移不从 1 开始,从 0 开始
// for (let i = 1; i <= len1; i++) {
// f[i][0] = (s1[i - 1] === s3[i - 1])
// if (f[i][0] === false) { // 有字符不匹配了,后面的就不可能匹配上
// break
// }
// }
// for (let i = 1; i <= len2; i++) {
// f[0][i] = (s2[i - 1] === s3[i - 1])
// if (f[0][i] === false) {
// break
// }
// }
// for (let i = 1; i <= len1; i++) {
// for (let j = 1; j <= len2; j++) {
// const x = i - 1, y = j - 1
// f[i][j] = (f[i - 1][j] && (s1[x] === s3[x + y + 1])) || (f[i][j - 1] && (s2[y] === s3[x + y + 1]))
// }
// }
// 动态转移不从 1 开始,从 0 开始
for (let i = 0; i <= len1; i++) {
for (let j = 0; j <= len2; j++) {
const x = i - 1, y = j - 1
if (i > 0) {
// 这里就要加上自己去或了
f[i][j] = f[i][j] || (f[i - 1][j] && (s1[x] === s3[x + y + 1]))
}
if (j > 0) {
f[i][j] = f[i][j] || (f[i][j - 1] && (s2[y] === s3[x + y + 1]))
}
}
}
return f[len1][len2]
}
// 动态规划 - 空间优化(滚动数组的思想)
// 空间小了 3MB 时间多了 4ms
// 老实说,懂了滚动数组的思想,但单独写代码写不出来,只能按照未优化的代码去改写
var isInterleave = function(s1, s2, s3) {
// 不用管交错的,直接一个字符一个字符接着匹配就行
// 主要是看 s3 的字符能不能和 s1/s2 的字符匹配
// f(i, j) - s1[1~i] 和 s2[1~j] 能否交错组成 s3[1~i+j]
// 状态转移 - s3[i+j] 最后是和谁匹配的 s1[i] 还是 s2[j]
// (f(i - 1, j) && s1[i] === s3[i + j]) || (f(i, j - 1) && s2[j] === s3[i + j])
const len1 = s1.length
const len2 = s2.length
if (len1 + len2 !== s3.length) {
return false
}
const cur = new Array(len2 + 5).fill(false)
cur[0] = true
// 动态转移不从 1 开始,从 0 开始
for (let i = 0; i <= len1; i++) {
for (let j = 0; j <= len2; j++) {
const x = i - 1, y = j - 1
if (i > 0) {
cur[j] = cur[j] && (s1[x] === s3[x + y + 1])
}
if (j > 0) {
cur[j] = cur[j] || (cur[j - 1] && (s2[y] === s3[x + y + 1]))
}
}
}
return cur[len2]
}
var s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" // true
var s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" // false
var s1 = "", s2 = "", s3 = "" // true
var s1 = "db", s2 = "b", s3 = "cbb" // false
const res = isInterleave(s1, s2, s3)
console.log(res)
120_三角形最小路径和
120_三角形最小路径和
递归 + 记忆化 + DP,♀️ 必须秒懂!
/*
leetcode 120. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-104 <= triangle[i][j] <= 104
进阶:
你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题吗?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/triangle
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[][]} triangle
* @return {number}
*/
// 动态规划
var minimumTotal = function(triangle) {
// 自顶向下的最小路径 === 自底向上的最小路径(不用考虑边界问题)
// f(i, j) - 自底向上的路径的最小值
// 状态转移 - 下到上
// f(i ,j) = min(f(i+1, j), f(i+1, j+1)) + triangle(i, j)
const m = triangle.length // [][0]
const n = triangle[m - 1].length // [0][]
const f = new Array(m).fill(0).map(() => new Array(n).fill(0))
for (let i = 0; i < n; i++) {
f[m - 1][i] = triangle[m - 1][i]
}
for (let i = m - 2; i >= 0; i--) {
for (let j = 0; j <= i; j++) {
f[i][j] = Math.min(f[i + 1][j], f[i + 1][j + 1]) + triangle[i][j]
}
}
return f[0][0]
}
// 动态规划 - 空间优化(滚动数组思想)
// 空间小了 2MB 时间多了 16ms
var minimumTotal = function(triangle) {
// 自顶向下的最小路径 === 自底向上的最小路径(不用考虑边界问题)
// f(i, j) - 自底向上的路径的最小值
// 状态转移 - 下到上
// f(i ,j) = min(f(i+1, j), f(i+1, j+1)) + triangle(i, j)
const m = triangle.length // [][0]
const n = triangle[m - 1].length // [0][]
const cur = new Array(n).fill(0)
for (let i = 0; i < n; i++) {
cur[i] = triangle[m - 1][i]
}
for (let i = m - 2; i >= 0; i--) {
for (let j = 0; j <= i; j++) {
cur[j] = Math.min(cur[j], cur[j + 1]) + triangle[i][j]
}
}
return cur[0]
}
var triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
// triangle = [[-10]]
const res = minimumTotal(triangle)
console.log(res)
131_分割回文串
这题不是动态规划呀,先搁着,以后写回溯的时候再回头来看(搁置??)
/*
leetcode 131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
提示:
1 <= s.length <= 16
s 仅由小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-partitioning
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {string} s
* @return {string[][]}
*/
// 动态规划
var partition = function(s) {
};
139_单词拆分
139_单词拆分-官方
「手画图解」剖析三种解法: DFS, BFS, 动态规划 |139. 单词拆分
动态规划 + 记忆化回溯 逐行解释 python3
/*
leetcode 139. 单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-break
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
// 动态规划
var wordBreak = function(s, wordDict) {
// 拆分 s,等同于拼接 wordDict
// f(i) - s[0~i] 是否可由 wordDict 中的单词拼接而成
// 状态转移 - s[k~i] 是由 wordDict 中的单词拼接而成的
// f(i) = (f(i-1) && s[i] in wordDict) || (f(k) && s[k+1~i] in wordDict) || (f(0) && s[1~i] in wordDict)
// f(i-1) = (f(i-2) && s[i-1] in wordDict) || (f(k) && s[k+1~i-1] in wordDict) || (f(0) && s[1~i-1] in wordDict)
// 无法优化状态转移方程
const n = s.length
const f = new Array(n+1).fill(false)
f[0] = true
for (let i = 1; i <= n; i++) {
for (let j = 0; j < i; j++) {
const str = s.slice(j, i)
f[i] = f[j] && (wordDict.indexOf(str) !== -1)
if (f[i] === true) {
// 已经能够拼接了,就不需要再转移了
break
}
}
}
return f[n]
};
// 优化
// 检查一个字符串是否出现在给定的字符串列表中——哈希表
// 可以剪枝:如果分割点 k 到 i 的长度大于字典列表里最长的单词长度,则结束枚举
// 也可以使用字典树 Trie 来实现查找
// 还有一个优化方向:每次枚举 k 时,可以依据字典列表中的单词长度来枚举
// DFS、BFS 好像也可以
var s = "leetcode", wordDict = ["leet", "code"]
s = "applepenapple", wordDict = ["apple", "pen"]
s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
const res = wordBreak(s, wordDict)
console.log(res)
152_乘积最大子数组
152_乘积最大子数组-官方
/*
leetcode 152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-product-subarray
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[]} nums
* @return {number}
*/
// 动态规划
var maxProduct = function(nums) {
// 代码错误
// f(i) - nums[0~i] 这些数中,连续子数组(包含 nums[i])的乘积最大值
// 状态转移 - 要不要 nums[0~i-1]
// f(i) = max(nums[i], f(i-1)*nums[i])
const n = nums.length
const f = []
f[0] = nums[0]
let res = f[0]
for (let i = 1; i < n; i++) {
f[i] = Math.max(nums[i], f[i - 1] * nums[i])
res = Math.max(res, f[i])
}
return res
// 代码错误
}
/*
上面的代码是参考的 53_最大子序和 的思路
但加和乘是不同的,加具有递增性(前面的负数就可以舍弃),
但乘不具备(前面的负数和当前的负数相乘可能是最大值)
[-2,3,-4] - 24,但我输出的是 3,因为舍弃了前面的 -6
*/
// 需要记录下最大和最小的连续子数组的乘积(最小-负数)
var maxProduct = function(nums) {
// fMax(i) = max(fMax(i-1)*nums[i], fMin(i-1)*nums[i], nums[i])
// fMin(i) = min(fMax(i-1)*nums[i], fMin(i-1)*nums[i], nums[i])
const n = nums.length
const fMin = []
const fMax = []
fMin[0] = fMax[0] = nums[0]
let res = nums[0]
for (let i = 1; i < n; i++) {
fMin[i] = Math.min(nums[i], fMin[i - 1] * nums[i], fMax[i - 1] * nums[i])
fMax[i] = Math.max(nums[i], fMin[i - 1] * nums[i], fMax[i - 1] * nums[i])
res = Math.max(res, fMax[i])
}
return res
}
// 然后可以进行空间优化
var nums = [2,3,-2,4]
// var nums = [-2,0,-1]
// var nums = [-2,3,-4]
const res = maxProduct(nums)
console.log(res)
由于存在负数,会导致最大的变最小的,最小的变最大的。因此还需要维护当前最小值 fMin
198_打家劫舍
198_打家劫舍-官方
/*
leetcode 198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 400
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/house-robber
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[]} nums
* @return {number}
*/
// 动态规划
var rob = function(nums) {
// f(i) - 考虑 nums[1~i],能偷窃到的最高金额
// 状态转移 - nums[i] 是否偷窃
// f(i) = max(f(i-1), nums[i] + f(i-2))
let f = []
f[0] = 0
f[1] = nums[0]
const n = nums.length
for (let i = 2; i <= n; i++) {
f[i] = Math.max(f[i - 1], nums[i - 1] + f[i - 2])
}
return f[n]
}
// 动态规划 - f(i) 另外一种定义
// f(i) - 考虑 nums[1~i],且必偷窃 nums[i] 的情况下,能偷窃到的最高金额
// 状态转移 - 倒数第二个是偷窃谁家的
// f(i) = nums[i] + max(f(i - 2), f(i - 3), f(k), f(1))
// f(i-1) = nums[i-1] + max(f(i - 3), f(i - 4), f(k), f(1))
// f(i) - nums[i] = max(f(i - 2), f(i - 1) - nums[i - 1])
// 最后的结果必须比较每个 f(i),返回最大值
var rob = function(nums) {
let f = []
f[0] = 0
f[1] = nums[0]
const n = nums.length
let res = nums[0] ? nums[0] : 0 // nums 为空则 res = 0
for (let i = 2; i <= n; i++) {
f[i] = nums[i - 1] + Math.max(f[i - 2], f[i - 1] - nums[i - 2])
res = Math.max(res, f[i])
}
return res
}
/*
状态的定义会影响状态转移方程
第二种的定义就比第一种的定义要细致一点,也就会复杂一点
第一种的定义更贴近题意
*/
// 可以进行空间优化(滚动数组思想)
var nums = [1,2,3,1]
var nums = [2,7,9,3,1]
var nums = [2,1,1,2] // 4
var nums = [] // 4
const res = rob(nums)
console.log(res)
213_打家劫舍II
打家劫舍 II(动态规划,结构化思路,清晰题解)
/*
leetcode 213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [0]
输出:0
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/house-robber-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {number[]} nums
* @return {number}
*/
// 动态规划
// 与打家劫舍 I 相比,就是偷窃第 n 家,不偷窃第 1 家,或,偷窃第 1 家,不偷窃第 n 家
// 拆成两个数组就行了
var rob = function(nums) {
// 复用一下代码 - 空间优化后的
var myRob = function(nums) {
// f(i) - 考虑 nums[1~i],能偷窃到的最高金额
// 状态转移 - nums[i] 是否偷窃
// f(i) = max(f(i-1), nums[i] + f(i-2))
const n = nums.length
let pre = 0, cur = nums[0]
for (let i = 2; i <= n; i++) {
const tmp = Math.max(cur, nums[i - 1] + pre)
// [pre, cur] = [cur, tmp] // 这样的写法,会报错 Cannot access 'tmp' before initialization
pre = cur
cur = tmp
}
return cur
}
const n = nums.length
// 特判一下
// 使用三元表达式,或多个 if
return n === 0 ? 0 : (
n === 1 ? nums[0] : (
Math.max(myRob(nums.slice(0, n-1)), myRob(nums.slice(1, n)))
)
)
if (n === 0) {
return 0
}
if (n === 1) {
return nums[0]
}
if (n === 2) {
return Math.max(nums[0], nums[1])
}
return Math.max(myRob(nums.slice(0, n-1)), myRob(nums.slice(1, n)))
}
var nums = [2,3,2]
var nums = [1,2,3,1]
// var nums = [0]
const res = rob(nums)
console.log(res)
221_最大正方形
221_最大正方形-官方
/*
leetcode 221. 最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:

输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
/**
* @param {character[][]} matrix
* @return {number}
*/
// 动态规划
var maximalSquare = function(matrix) {
// f(i, j) - 以 (i, j) 为终点(右下角)的最大正方形的边长
// 状态转移 matrix(i, j)===1 f(i, j)=min(f(i-1, j-1), f(i-1, j), f(i, j-1)) + 1
const n = matrix.length // [][0]
const m = matrix[0].length // [0][]
let res = 0
let f = new Array(n).fill(0).map(() => new Array(m).fill(0))
// 先初始化,把第一行/列的正方形标记出来
for (let i = 0; i < n; i++) {
if (matrix[i][0] == 1) {
f[i][0] = 1
res = 1
}
}
for (let i = 0; i < m; i++) {
if (matrix[0][i] == 1) {
f[0][i] = 1
res = 1
}
}
// 进行状态转移
for (let i = 1; i < n; i++) {
for (let j = 1; j < m; j++) {
if (matrix[i][j] == 1) {
f[i][j] = Math.min(f[i - 1][j - 1], f[i][j - 1], f[i - 1][j]) + 1
res = Math.max(f[i][j], res)
}
}
}
return res * res
}
// 动态规划 - 在 matrix 上原地修改
var maximalSquare = function(matrix) {
// f(i, j) - 以 (i, j) 为终点(右下角)的最大正方形的边长
// 状态转移 matrix(i, j)===1 f(i, j)=min(f(i-1, j-1), f(i-1, j), f(i, j-1)) + 1
const n = matrix.length // [][0]
const m = matrix[0].length // [0][]
let res = 0
// 初始化 res
// for (let i = 0; i < n && res === 0; i++) {
// for (let j = 0; j < m && res === 0; j++) {
// if (matrix[i][j] == 1) {
// res = 1
// }
// }
// }
for (let i = 0; i < n && res === 0; i++) {
if (matrix[i][0] == 1) {
res = 1
}
}
for (let i = 0; i < m && res === 0; i++) {
if (matrix[0][i] == 1) {
res = 1
}
}
// 进行状态转移
for (let i = 1; i < n; i++) {
for (let j = 1; j < m; j++) {
if (matrix[i][j] == 1) {
matrix[i][j] = Math.min(matrix[i - 1][j - 1], matrix[i][j - 1], matrix[i - 1][j]) + 1
res = Math.max(matrix[i][j], res)
}
}
}
return res * res
}
var matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
var matrix = [['0']]
const res = maximalSquare(matrix)
console.log(res)
嘎嘎,前端有趣,一起努力