旅行商问题之状压DP——旅行商变体之贪心法——旅行商问题之思考&&比较遗传算法退火算法_——重新补最短路基础未完成—— A Journey to Greece
部分目录
-
- Unsolved 18 / 85 A Gym 100753A A Journey to Greece
-
- 官方题解:TSP变体
- TSP问题——大名鼎鼎的旅行商问题解法
-
- 方法1:状压DP法
- 附:遗传算法的乌龙
- 刚刚在上面发现一个新问题:状压DP不能保证每个点只走一次?
-
- 那么有一个解决方法,如果要只经过一次的话,也就是只给状压经过,求最短路时不要经过(只不重复要参观的城市):
- 我们是不是可以不重复所有的城市?(超时超空间,,解决,,可能要调数据范围AC)
- 对于标准的TSP,我们是否可以不管重复不重复,只要走过所有点的最短路?
- 有没有什么办法可以点对点求最短路或者点对若干点求最短路?
- 恰遇变体:贪心法解
-
- 小哥登场
- 变体与原板的区别:
- 是否可以自己想一个找方向的方法用A*算法优化旅行商问题?(有解决思路,还可能是旅行商问题K短路的解法)
-
- 如何改正确?
- 重新补最短路基础(未完成)
- 智能算法如何找方向的?
- 附:给Pecco学姐的讨论信
来源题解目录
比赛link
Unsolved 18 / 85 A Gym 100753A A Journey to Greece
题意:
我想从0点出发,游览若干个指定点,在指定时间回到0点,我有一张出租车车票,可以任意从一点到另一点,问是否能按时,是否要出租车车票才按时?
若不在某个点游览,就不计在该点等车时间
输入:
有N个位置节点,P个景点想去,M是(无向)路的数量,G是给的总时间,T是出租车花的时间
接下来P行是这个节点序号和逗留时间
接下来M行是路的端点和该路花的时间
需要注意的范围是:
1 ≤ N ≤ 2 · 104
1 ≤ P ≤ 15 ——只有15
1 ≤ M, G ≤ 105
1 ≤ T ≤ 500
思路:
首先是比较有趣有用的一道题
首先不用出租车怎么判断都不太清楚
先不用出租车找最短路
但是Dijkstra算法我是学了的,在上面
可不可以贪心?
P次dj算法,每次去取最短路?
可能不太好,会不会有局部最优的情况
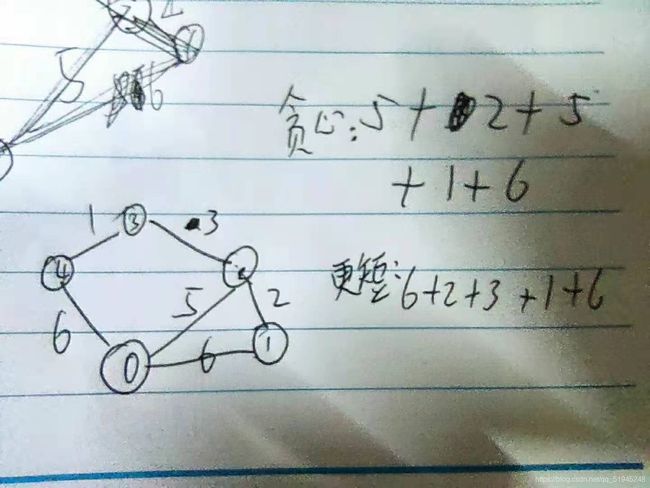
那就明天再看吧
转眼间过了几天,我又回来啦
这个题已经不简单了,但是花时间应该还是可以明白
官方题解:TSP变体
看题解,搜TSP,发现这个就是大名鼎鼎的旅行商问题
的变体
如果没有这个TAXI,就几乎是准旅行商问题:
旅行商问题,即TSP问题(Traveling Salesman
Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
之所以还不是准旅行商问题,是因为这里只要访问部分的地点
官方题解上说,P次Dijkstra算法,让每个要走的节点中都是最短路
如果没有出租车就进行TSP了
目前表述是,
- Compute shortest paths by P-times Dijkstra: O(P · N log N)
——这个是上面说的化为标准TSP - Run 2P DP solution for TSP — P! will be to slow
——接下来要搞懂这个次数是什么意思,先学TSP,看上去是DP - Add extra dimension to the DP to account for the taxi ticket
——如何增加维数,车票只能用一次,可能是每两个P内的点加一条用车票的边,来一次dj
这好像就是那P!(?)那怎么改进成2p 呢? - Compare the two values with G − ∑ \sum ∑ti
——比较什么呢,G是给的总时间, ∑ \sum ∑ti可能是各次都要看
TSP问题——大名鼎鼎的旅行商问题解法
旅行推销员问题是图论中最著名的问题之一
描述:
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
即
“已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路”
——但是至少状压DP用的dj最短路会让节点不一定经过一次,如
4 3 6 18 1
1 0
2 0
3 0
0 1 4
1 2 4
1 3 4
0 2 100
0 3 100
2 3 100
结果:
不Taxi是24————是要走重复点的
Taxi是17
(好在这题没有要求只走一次)
Pecco学姐没有写这个,她在CF上回道
“啊,谢谢w
旅行商没专门写过呢,那个一般用状压DP做,如果以后要写状压DP可能写一写吧(”
之前看了好多她的,,真的很容易懂,超赞的
观察了一下,是个难问题
贪心算法,近似算法不够准,
蚁群算法,遗传算法较慢,且代码长
B站PY实现的很好的遗传算法讲解视频
外国的讲师,c++实现
没想到就要学神经网络的算法了,真是深又易得
这是个难题,感觉一路走来一步步在攀登高峰
先了解到这里,要去期中考试了,周末再学
忍不住又看了一下,Pecco学姐不是说用状压DP吗
还是这个简单
TSP问题之状压dp法,https://www.cnblogs.com/real-l/p/8589562.html
好的现在我们开始学:
方法1:状压DP法
假设这个n很小,我们就可以使用状态压缩的方法求解,在一般的TSP问题中的用状压求解的题目,我们可以定义一个dp数组,dp[i][v],其中v表示一个集合,dp[i][v]表示到i这个点经过v中所有点的最小路径.
假设我们从s出发,最后再回到s
1.那么最开始,只有dp[s][{s}]=0,其余均等于inf
2.其他情况下,dp[i][state]=min(dp[i][state],dp[j][state’]+c[j][i])
3.最后我们的结果,ans=min(ans,dp[i][state]+c[i][s]),因为我们要求的是一个环的最短路,所以还要加上回来的距离
那么还有一个问题,我们要如何存下这个集合,当然是用状态压缩的方法,s|1<<(k),表示由原来的状态s转移到加上k这个点的状态,那么就很好求解了对吧
官方代码一:(我还没看,不过应该懂了,要去期中考试了,周末再学)
(交一下,爆空间了)
#include
#include
if (dp[(1<<nS)-1][0][1] > G) cout << "impossible" << endl;
else if (dp[(1<<nS)-1][0][0] <= G) cout << "possible without taxi" << endl;
else cout << "possible with taxi" << endl;
}
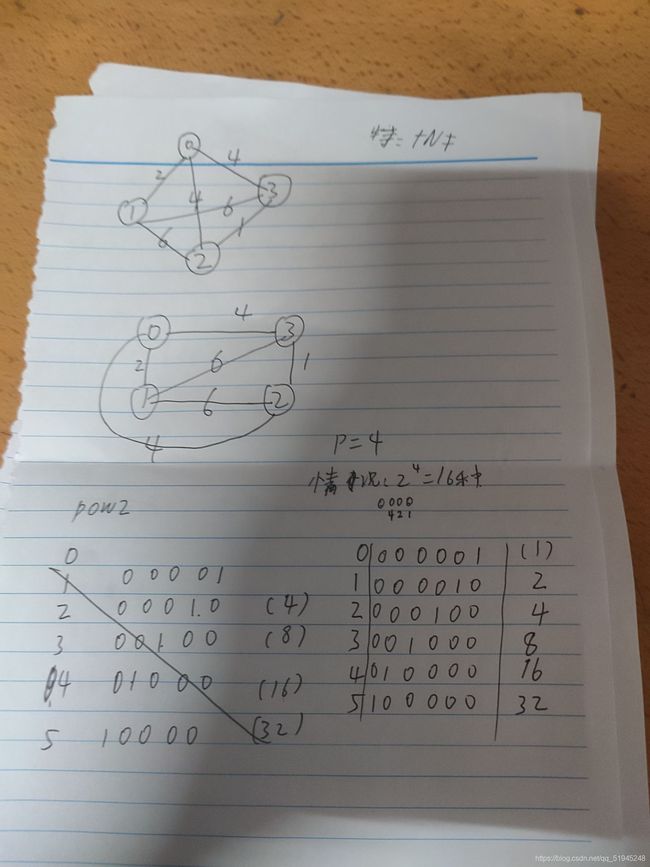
官方AC代码,用的是可变数组:
原始,1887ms
#include 略有修改,421ms
看懂了有了注释
#include 全过程在此,整整花了四面:

简单,尽管时间复杂度可能更大,不过是最能理解实现的了ww
官方的题解2n意思可能也是说状压DP吧,看来ACM还没那么鬼畜。。
也许是暂时没有,真的到了顶上,可能要写一大串效率较高的遗传算法www
自己写了,186ms最快,不知道为什么
2处wa,
一个是认真数数——0到p是p+1个城,但加上出租车虚拟节点是P+2个城要二进制
一个是G因为修改多减一次了——修改了要注意去改
/*题意:
我想从0点出发,游览若干个指定点,在指定时间回到0点,我有一张出租车车票,可以任意从一点到另一点,问是否能按时,是否要出租车车票才按时?
若不在某个点游览,就不计在该点等车时间
输入:
有N个位置节点,P个景点想去,M是(无向)路的数量,G是给的总时间,T是出租车花的时间
接下来P行是这个节点序号和逗留时间
接下来M行是路的端点和该路花的时间
需要注意的范围是:
1 ≤ N ≤ 2 · 10^4^
1 ≤ P ≤ 15 ——只有15
1 ≤ M, G ≤ 10^5^
1 ≤ T ≤ 500
官方题解上说,P次Dijkstra算法,让每个要走的节点中都是最短路
如果没有出租车就进行TSP了
目前表述是,
- Compute shortest paths by P-times Dijkstra: O(P · N log N)
——这个是上面说的化为标准TSP
- Run 2^P^ DP solution for TSP — P! will be to slow
——接下来要搞懂这个次数是什么意思,先学TSP,看上去是DP
- Add extra dimension to the DP to account for the taxi ticket
——如何增加维数,车票只能用一次,可能是每两个P内的点加一条用车票的边,来一次dj
这好像就是那P!(?)那怎么改进成2^p^ 呢?
- Compare the two values with G ?$\sum$ti
——比较什么呢,G是给的总时间,$\sum$ti可能是各次都要看
方法1:状压DP法
假设这个n很小,我们就可以使用状态压缩的方法求解,在一般的TSP问题中的用状压求解的题目,我们可以定义一个dp数组,dp[i][v],其中v表示一个集合,dp[i][v]表示到i这个点经过v中所有点的最小路径.
假设我们从s出发,最后再回到s
1.那么最开始,只有dp[s][{s}]=0,其余均等于inf
2.其他情况下,dp[i][state]=min(dp[i][state],dp[j][state']+c[j][i])
3.最后我们的结果,ans=min(ans,dp[i][state]+c[i][s]),因为我们要求的是一个环的最短路,所以还要加上回来的距离
那么还有一个问题,我们要如何存下这个集合,当然是用状态压缩的方法,s|1<<(k),表示由原来的状态s转移到加上k这个点的状态,那么就很好求解了对吧
*/
#include
#define pdd pair
#define vii vector
#define st first
#define nd second
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define _forplus(i,a,b) for( register int i=(a); i<=(b); i++)
#define forplus(i,a,b) for( register int i=(a); i<(b); i++)
#define _forsub(i,a,b) for( register int i=(a); i>=(b); i--)
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f
#define pi (acos(-1))
#define EPS 0.00000001
#define MOD 1000000007
#define fastio std::ios::sync_with_stdio(false);std::cin.tie(0);
int N, P, M, G, T, p[17], t[17], s, d, cost, dist[17][20000], m[17][17], opt[65536*2*2][17], pow2[18];
vector<int> adjList[20000], costList[20000];
void dj(int i){
//可变数组式,i号点
fill_n(dist[i],N,INF);
dist[i][p[i]]=0;
priority_queue<pii,vector<pii>,greater<pii> >q;
q.push(pii(0,p[i]));
while(!q.empty()){
pii te=q.top();q.pop();
if(te.st>dist[i][te.nd])continue;
forplus(k,0,adjList[te.nd].size()){
if(dist[i][adjList[te.nd][k]]>te.st+costList[te.nd][k]){
dist[i][adjList[te.nd][k]]=te.st+costList[te.nd][k];
q.push(pii(dist[i][adjList[te.nd][k]],adjList[te.nd][k]));
}
}
}
}
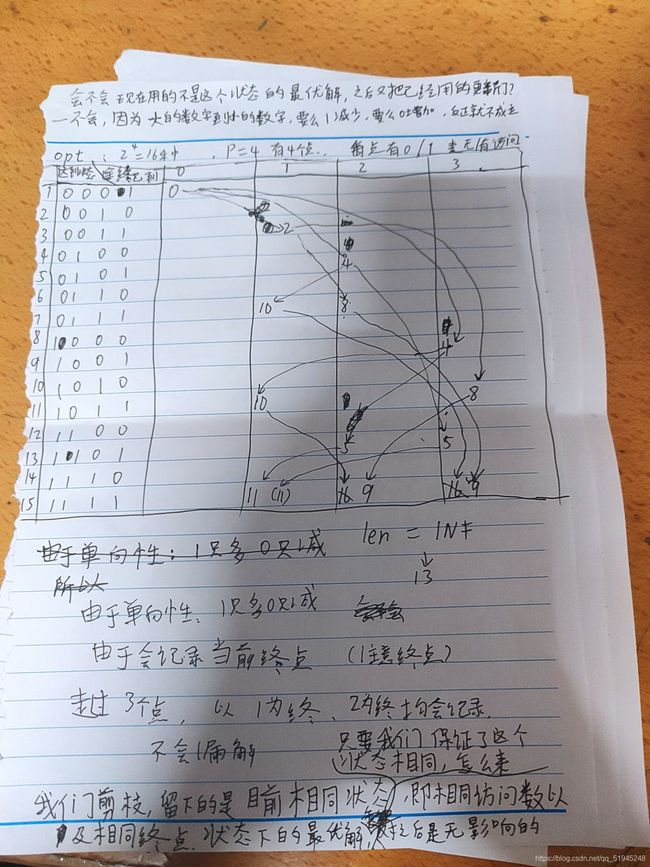
int solve(){
_forplus(i,1,pow2[P+1]){
fill_n(opt[i],P+1,INF);
}
opt[1][0]=0;
forplus(i,1,pow2[P+1]){
_forplus(j,0,P){
if(opt[i][j]==INF){
continue;
}
_forplus(k,0,P){
if((i>>k&1)||m[j][k]==INF)continue;
if(opt[i][j]+m[j][k]<opt[i+pow2[k]][k]){
opt[i+pow2[k]][k]=opt[i][j]+m[j][k];
}
}
}
}
int len=INF,now=pow2[P+1]-1;
_forplus(i,1,P){
if(opt[now][i]+m[i][0]<len){
len=opt[now][i]+m[i][0];
}
}
// cout<
return len;
}//从0到p共p+1个,从0点出发,0000001表示第0位第0号 ,返回长度
int main(){
fastio
cin>>N>>P>>M>>G>>T;
p[0]=t[0]=0;
_forplus(i,1,P){
cin>>p[i]>>t[i];
G-=t[i];//为了结构好看到了这里,就要回去检查不要遗留在Dj里
}
_forplus(i,1,M){
cin>>s>>d>>cost;
adjList[s].pb(d);
costList[s].pb(cost);
adjList[d].pb(s);
costList[d].pb(cost);
}
mem(m,0x3f);
_forplus(i,0,P){
dj(i);
_forplus(k,0,P){
m[i][k]=dist[i][p[k]];
//cout<
}
}
pow2[0]=1;
_forplus(i,0,P+1){
//注意数数,0到P加出租车节点,共P+2个
pow2[i+1]=pow2[i]<<1;
//cout<
}
if(solve()<=G){
cout<<"possible without taxi"<<endl;
}else{
P++;
forplus(i,0,P)m[i][P]=T;
forplus(i,0,P)m[P][i]=0;
m[P][P]=0;
if(solve()<=G){
cout<<"possible with taxi"<<endl;
}else{
cout<<"impossible"<<endl;
}
}
return 0;
}
附:遗传算法的乌龙
有时间再学
先去cf上看看有没有这样的C++代码
好像。。。没有
好像那一大串代码跑起来,至少在n较小的时候,还没有状压DP快
因为那都是规定了跑几代的吧
并且最让人迷惑的是跑起来参数自己定,没看到个标准公式判断那样才能取正确解或者效率最高的解。。
博士说:
会比状压快,但是是近似算法,不一定能得到最佳
看到200多行遗传代码,还是不一定最优的,还是先不学了吧ww
但是这只是一个板子题,就算理解已经难了,还要多创新思想,不会只考板子,要打开思路
刚刚在上面发现一个新问题:状压DP不能保证每个点只走一次?
不对,我懂了些什么,是只对这个变体,要用到最短路的情况下,才会有这重复的情况。
如果是纯给一个图,状压DP是不可能走回去的
——上面已经证明了
但是有没有既能用最短路,又不重复走呢?
这种事情在现实生活中蛮多的,
虽然最近的就好,不能重复走着实离谱
但是有没有可能既是多个地点里选几个节点,又不能重复走呢?
毕竟旅行商问题也不许重复走也很离谱啊
就是说,我们是否可以不管重复不重复,只要选走过了所有点的最短路?
总之
状压DP让旅行商问题不可能重复,因为数字由小变大。每个点经历一次。
而是这个变体,DJ算法,该出发点经过了其他的点到达了其他旅行要经过的点,其他的点包括旅行要经过的点
——用了这个就多了一次经过
那么有一个解决方法,如果要只经过一次的话,也就是只给状压经过,求最短路时不要经过(只不重复要参观的城市):
我们不让TSP的图上边是经过了其他点的
即求最短路的时候加一个判断,如果
——但是这个方法是不重复要参观的城市,不是不重复任何城市,原因还是一样:
该出发点经过了其他的点到达了其他旅行要经过的点,那这个其他的点只就可能被用多次
forplus(k,0,adjList[te.nd].size()){
//若要求每个要参观的城市只经过一次,就在这里插入:
// if( 判断:adjList[te.nd][k] in p) continue;
//——这个在要参观的城市内,就只留到最后算走一次,不然用到了就重复
if(dist[i][adjList[te.nd][k]]>te.st+costList[te.nd][k]){
dist[i][adjList[te.nd][k]]=te.st+costList[te.nd][k];
q.push(pii(dist[i][adjList[te.nd][k]],adjList[te.nd][k]));
}
我们是不是可以不重复所有的城市?(超时超空间,,解决,,可能要调数据范围AC)
这个就更难了,因为要参观的城市还能只让最后走一次即DJ时不要算,这个不能固定
在哪条路上走最多一次?
这样子,我们在DJ时记录父节点,
之后在新图中的每条边就有经过了哪些老节点,老节点即未指定的所有节点
之后我们DP中的每一个状态(经过多少城市与终点为何)元素,
都带有一个vis数组记录到这个状态经过了各点几次,元素个数是老节点个数,各元素初始为0,
每要走一条边就试图更新一次,如果更新后其中有大于1的元素就要放弃这条路了,就是重复走了。
对于标准的TSP,我们是否可以不管重复不重复,只要走过所有点的最短路?
可以的,这里反着来,先DJ,弄一个新图,再状压,就无谓次数了。
刚刚在研究在哪里插入判断的时候想到,每次DJ我们只需要到P(15)个点的最短路,可是我们却判断了到N(2e4)个点的最短路。有没有什么办法可以点对点求最短路或者点对若干点求最短路?
有没有什么办法可以点对点求最短路或者点对若干点求最短路?
目前网上只流传着一个点到多点的算法:DJ和SPFA优化
感觉有点像没有第一层怎么来第三层的感觉
讲道理有点人生不经历失败那能成功的感觉hhh
不过从floyd到bella-floyd到spfa到dijkstra都是创新的过程,都有点没有第一层来了第三层的感觉
我们是不是可以发明出点对点的更快的方法!!!
就像米勒罗宾素数判定
线性筛哪知道可以不靠之前的数就能很快知道这个是不是素数啊_
感觉超级有用的
只是现在还没有一点头绪www
算法导论:目前点对点的算法,时间复杂度最慢和单源的最优算法一样
也就是说有是有,不一定够快
如果不是只求1~2个,时间还更浪费了。。
暂时放下吧
恰遇变体:贪心法解
旅行商问题C. Travelling Salesman Problem
100000个节点
不可能是状压DP
——状压DP实际上是剪枝暴力
我应该多思考
思考了一下就过一会再思考
每次思考10分钟有的时候就想到了
比一次思考30分钟看代码答案
要锻炼思维
希望这是最后一次思考了不到三次就去看代码的
以后知道方法了吗
题意:
有N个城市,分别有
from city i to city j costs max(ci,aj−ai)
ci是从i城出发的保底值,不是负数
aj-ai是j城的景象值-i城的景象值,显然到越美的城市花越多钱,对的
官方题解
意思是什么
再想想
1.可以无视起点,
故可以按美丽值排序
2.max(ci,aj-ai)=ci+max(0,aj-ai-ci)
ci是固定至少的消费,只要后面的和min
3 .
1)只看后面,则从aj<=ai的后面的城市i到j肯定是免费的
2)当aj<=ai+ci也是免费的,判断的话由aj是固定的,只要看aj的最大值。这个最大值之后的就是不免费了
那
对于1),我们只要存下i到j的边就是能走最远的0了
对于2),我们只要存下i到j+1的边就是最有可能消耗地少的有花费了
这样子我们就可以跑从a1到an的最短路
这就是min的sum,因为再走回来都是免费,更因为必须要从a1到an一次
4 .
可以做一个简化,
因为每个点都是从之前的点来,所以我们接到之前花费最少且现在花费最少
现在花费最少就接到之前a+c最大
之前花费最少,需要接到的点也是花费最少的
接到的点又由选它接到的花费最小的点
倒爬的贪心!!线性时间复杂度
从第二个点开始循环
每多走一个i点,要多花max(0,ai-max(aj+cj)j
为什么
因为这是一个树状的结构,每个点从最近的那个地方来
举例
a 0 2 3 4 7 8
c 1 3 0 2 1 4
增加 1 0 0 1 0
这样子(以a看)2从0来,3,4从2来,7从6来,8从7来
到头来8还是从0来
选花费最小的接点的技巧
保存之前的max和现在的前一个比较
而不用个个都比较,那样重复了
#include
#define pdd pair
#define vii vector
#define st first
#define nd second
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define _forplus(i,a,b) for( register int i=(a); i<=(b); i++)
#define forplus(i,a,b) for( register int i=(a); i<(b); i++)
#define _forsub(i,a,b) for( register int i=(a); i>=(b); i--)
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f
#define pi (acos(-1))
#define EPS 0.00000001
#define MOD 1000000007
#define fastio std::ios::sync_with_stdio(false);std::cin.tie(0);
#define N 100005
pll a[N];
int main(){
fastio
ll sum=0,n;
cin>>n;
_forplus(i,1,n){
cin>>a[i].st>>a[i].nd;
sum+=a[i].nd;
}
sort(a+1,a+1+n);
ll ma=a[1].st+a[1].nd;
_forplus(i,2,n){
if(a[i-1].st+a[i-1].nd>ma){
ma=a[i-1].st+a[i-1].nd;
}
sum+=max(0LL,a[i].st-ma);
}
cout<<sum;
return 0;
}
小哥登场
小哥写的题解,比官方题解好看懂多了
小哥:
1.化max为一个常数加0和差的比较,ai-aj-cj
2.免费和计费,只要到ai最大的点,
按ai降序走一遍未经过的点回起点,不会产生任何花费
计算到最大ai即可
3.路径本质上是一个由有向边组成的环,求环上的边权和
环无谓起点,因为就算开始是最大的点,往下走没有花费,还是得走回去的
那么求的是从a最小的点走到a最大的点就可以了
4.先排序a,再贪心求解
小哥:
过程可以设计为:从最小点出发,走到最大点,当在某一点i时,直接走到i后面a最大且值小于max(ak+ck)的点q(k表示所有在q前面的点),其中i到q上的所有点我都可以免费的扩展到。然后再从q出发重复这个过程,如果没有符合条件的q,那么就需要花费代价扩展到q的下一个点.
是的,这样的理解方式更容易理解,正序,能不多花就不多花的贪心,很易懂
变体与原板的区别:
原版是暴力加剪枝,用到变体上肯定是正确解,但是时间空间远远不达标
变体是有一个类似于势能的ai,问在山上走遍一些标记点要多少体力
联系生活,原板求解相当于山上几次山下几次,而生活规律告诉我们这是有方向的
问从山腰到山顶到山脚再到山腰要多少体力
我们求的就是有方向的山脚到山顶了
ci+max(0,aj-(ai+ci))
在max中,aj,ai是各自高度,ci相当于在i点的助推器,高度差超过了ci就要体力
之后就化成了贪心问题,从山脚,看最多能助推到哪里,这样看
化无向为有向,不仅让人想到了A*算法
创新的,我们是否可以对原板状压DP做改进?
——遗传算法,退火算法等智能算法就是寻找方向
想不想知道如何找方向的?
想不想自己想一个新的找方向的方法?
是否可以自己想一个找方向的方法用A*算法优化旅行商问题?(有解决思路,还可能是旅行商问题K短路的解法)
A*是否有效,关键在于找方向的方法,找的越好,越快越准
比如直角坐标系下是x+y+z还是sqrt(x2+y2+z2)
但是旅行商问题,各状态都要有根据的话…
那要如同状压DP里,每个状态点的离结束的距离都要算出来吗
弄不好这个预处理时间花费是巨大的
连正规的TSP状压都有很多状态点能达不到,能忽略不看
然而经过多少点与现在在哪个位置,可能是必须要考虑的变量
所有就不知道怎么办
有点猴子打字的感觉哈哈哈
有一点想法了,
我们进行有优先级的BFS,用堆来优化
到达了的终点和已经走的城市仍然是继续往下的依据,且可以去重
状压DP是盲目看每一个状态
这里有优先级判断标准:离起点的距离少和已经走过的城市数多的加权评分
取路的总长求平均数,作为每走过一个城市能减多少计算的距离
这个初期的想法并不能保证这个方向正确,容易陷入局部最优解
并且还有走回来一茬,如果只是一笔画不走回来,这个还有一定道理
当然也能很容易被WA
比如
有的路是50 50 50
有的路是100 1 1
每多经过一个城市减10距离
会选择前者
而后者是更优的,
只是我们没有计入后面的是小1,能减许多距离,而是粗略的一个城市-10
那我们记录了到终点的正确距离,就是关键
那再来一条改进:
到一个城市后,加入它可以到达的点的min为权
那其实还是走了50 的路,相当于把即时判断改为提前判断了而已。。
如何精确找到终点的距离:
各直接和终点相连的点到终点的距离可以知道——图中的边
那倒数第二个点到终点,就是那些点到倒数第一个点的距离加倒数第一个点到终点的距离
也就是要一个表状态的二进制的数和表所在点的数组合而成的二维数组
这么倒着来,最后所有可能到达状态的离终点的距离就知道了
连全0状态到终点的距离也出来了
好像我发现了一个K短旅行商问题的解法,这作为预处理
时间复杂度上,是P!,过程像极了朴素的DFS求旅行商问题
但是可以剪枝,模仿这个状压DP
怎么设计剪枝?
借鉴状压DP,相同状态只保留最优解
我们从11111111…倒回来
也是相同状态,只保留最优解
预进行一次状压DP,与K短路预进行一次dijkstra极其类似
难道A*算法一般都是从终点倒爬一次得出各点到终点的距离?
很可能
这个怎么解旅行商问题的K短路?
还是有点难,要考虑如何保证走过所有点
——那就错了,我们剪枝就剪掉了一些次优解
如何改正确?
我们是怎么解决A* 算法K短路的?
在BFS中,第一次到达终点就是到终点的最短路,那么第k次到达终点,当然就是到终点的第k短路了
以A* 启发函数:f = x + h为排序,取出点
但是我不太能理解,从A* 到bfs 到Floyd 到spfa 都有点不懂,,只会写Dijkstra
那现在先重新补最短路问题,学好基础
重新补最短路基础(未完成)
智能算法如何找方向的?
认真看能看懂的:
模拟退火算法
遗传算法
缺陷:不够准
对比:
20
A B C D E F G H I J K L M N O P Q R S T
8 1 10 1 8 10 1 5 2 3 3 6 2 6 7 4 5 1 9 1
10 4 2 2 5 9 10 7 1 5 2 3 3 10 2 9 2 6 3 3
9 5 3 2 2 5 8 4 4 2 7 6 1 4 4 6 3 5 4 9
7 2 4 9 4 2 6 10 9 1 10 8 5 10 6 3 1 9 1 3
6 3 4 9 4 2 2 9 4 1 10 8 3 5 4 10 2 5 5 7
7 8 2 7 9 2 5 10 5 5 3 8 7 2 8 2 7 7 10 1
10 4 6 4 1 6 2 7 3 2 2 2 4 6 10 7 10 4 9 7
8 4 2 4 7 3 10 10 2 4 10 9 7 3 5 2 5 10 6 3
5 4 8 10 8 4 9 4 6 10 2 1 8 10 2 9 3 9 3 7
6 5 10 10 7 5 5 6 4 2 1 8 1 2 9 8 4 9 9 10
9 9 5 3 6 5 8 6 7 8 8 10 3 7 10 3 10 7 5 1
3 3 4 1 5 7 3 10 5 2 7 5 1 5 6 5 3 2 3 5
3 1 7 5 2 3 2 5 9 10 4 5 8 6 2 2 1 6 4 6
7 7 8 3 10 7 8 8 1 7 2 10 7 4 2 3 5 10 2 10
3 6 10 4 9 10 5 9 6 8 4 6 10 9 8 9 10 2 8 9
2 9 4 3 2 9 2 7 4 3 8 7 3 10 10 2 3 7 7 10
2 1 9 2 2 2 6 7 1 10 6 1 5 5 1 8 7 5 10 5
10 3 7 6 1 1 10 7 4 4 3 7 7 8 9 10 4 6 3 9
3 6 1 5 4 8 7 5 4 5 1 6 7 3 2 9 1 6 9 6
6 9 2 6 6 5 8 2 3 4 1 8 4 6 7 9 3 7 3 8
状压DP:
距离:27
路线:P<-F<-R<-O<-B<-Q<-M<-C<-H<-T<-K<-S<-D<-L<-I<-N<-J<-E<-G<-A<-begin
时间:0.7112s
退火算法:
****************************** TSP_SA - BestSolution ******************************
最优路径,bestSoluion.path[ ] = A-->R-->F-->C-->D-->S-->Q-->B-->I-->L-->G-->E-->M-->P-->J-->K-->T-->H-->N-->O-->A
最优路径,bestSoluion.length_path = 35
***********************************************************************************
程序运行时间 RunningTime = 0.197
注意,由于随机,所以每次结果不一样,基本上都在32到45之间。。离27差远了
样例:
5
1 2 3 4 5
12 32 23 23 23
12 21 23 43 34
32 12 34 54 65
23 34 34 34 34
3 34 344 34 4
状压DP:
距离:106
路线:5<-2<-3<-4<-1<-begin
--------------------------------
Process exited after 0.01482 seconds with return value 0
请按任意键继续. . .
有的时候遗传算法、退火算法也会有106的正确解,可能是数据小
退火算法:
****************************** TSP_SA - BestSolution ******************************
最优路径,bestSoluion.path[ ] = A-->E-->D-->C-->B-->A
最优路径,bestSoluion.length_path = 115
***********************************************************************************
程序运行时间 RunningTime = 2.341
请按任意键继续. . .
****************************** TSP_SA - BestSolution ******************************
最优路径,bestSoluion.path[ ] = A-->D-->C-->B-->E-->A
最优路径,bestSoluion.length_path = 106
***********************************************************************************
程序运行时间 RunningTime = 2.336
请按任意键继续. . .
遗传算法:
当前最优个体 bsetSolution = 1 -> 5 -> 4 -> 3 -> 2 -> 1 length = 115
【 程序运行时间 RunningTime = 2.275 】
请按任意键继续. . .
当前最优个体 bsetSolution = 1 -> 4 -> 3 -> 2 -> 5 -> 1 length = 106
【 程序运行时间 RunningTime = 2.168 】
请按任意键继续. . .
有的时候遗传算法、退火算法也会有106的正确解,可能是数据小
但是ACM来说,是不太行了
看上面的网站,可以大致了解了。暂时先放下吧。
现实生活中,出点误差,也是正常智能的行为。
附:给Pecco学姐的讨论信
To Pecco:
学姐晚上好啊~
你的小迷弟又来啦~
就上次我们讨论的旅行商问题,我有了一点创新的想法,有的想的到有的想不到,想和讲的东西非常喜欢听的Pecco学姐探讨一下w
并且说不定题目会这样变的w,虽然Pecco学姐比我厉害的多,但是看了说不定以后就更快想到解决方法了w
最近都在期中考试叭,如果没时间看就有时间再想没关系的啦,我也是,打算五一节左右想出来就好了
那下面请让我开始讲叭,谢谢你学姐:
上次的题目,GCPC2015区域赛 1970c121d675eab16d355104cb30e803 (z180.cn) 的A题
题意大致是:
一个无向地图(最多2e4个节点,1e5条边),从起点出发,经过指定点(小于15个),回到出发点,求最短路程。
(当然TAXI设虚拟节点也是很值得借鉴的啦,他有一张TAXI票)
官方解法:
先Dijkstra走出各指定点(包括起点)的最短路,构造了一个新图,节点是指定点,边是指定点间的最短路,成为一个标准TSP
再进行旅行商问题的状压DP解法(多谢学姐),也就是暴力加剪枝
下面是一些创新:
1.(已解决)如果要求一个指定点只访问一次?(现在指定点可能被访问多次)
——访问多次原因是求最短路会途径指定点,状压DP是只访问一次的。我们DJ求最短路时忽略经过指定点的边即可不途径指定点。
2.(超时超空间地解决了,,要调数据才AC)(我是和你写的时候写着写着想到的w感谢学姐)我们是不是可以不重复所有的城市?(同理现在也不能保证不重复所有的城市)
每个城市最多访问一次emmmm
我们在DJ时记录父节点
(我至今一想到你说的“其实很简单,只要一句话”和“只能追溯父节点”的倒爬就很激动欣喜)
之后在新图中的每条边就有经过了哪些老节点,老节点即未指定的所有节点
之后我们DP中的每一个状态(经过多少城市与终点为何)元素,
都带有一个vis数组记录到这个状态经过了各点几次,元素个数是老节点个数,各元素初始为0,
每要走一条边就试图更新一次,如果更新后其中有大于1的元素就要放弃这条路了,就是重复走了。
3.(已解决) 对于标准的TSP,我们是否可以不管重复不重复,只要走过所有点的最短路?
可以的,这里反着来,先DJ,弄一个新图,再状压,就无谓次数了。
4.(未解决)有没有什么办法可以点对点求最短路或者点对若干点求最短路?
感觉有点像没有第一层怎么来第三层的感觉
讲道理有点人生不经历失败那能成功的感觉hhh
不过从floyd到bella-floyd到spfa到dijkstra都是创新的过程,都有点没有第一层来了第三层的感觉
我们是不是可以发明出点对点的更快的方法!!!
就像米勒罗宾素数判定
线性筛哪知道可以不靠之前的数就能很快知道这个是不是素数啊^_^
感觉超级有用的
只是现在还没有一点头绪www
又通过一道旅行商问题的变体——贪心算法
https://codeforces.com/contest/1503/problem/C
{
哇,Pecco学姐也做了这题欸
我找到并拜读了学姐的代码w
Pecco学姐AC的时间是Apr/04/2021 15:20UTC+8
学姐的方法虽然比官方的DJ方法快很多
但还是可以改进成时间快一半的贪心哦:
DJ可以贪心为:
从a最小点出发,走到a最大点,
当在某一点i时,直接走到i后面a最大且值小于等于max(ak+ck)的点q(k表示所有在q前面的点,max会每次更新),其中i到q上的所有点我都可以免费的扩展到。
然后再从q出发重复这个过程,如果没有符合条件的q,那么就需要花费代价扩展到q的下一个点.
最后从a1到an的多花费是sum代价。
——这个过程是线性的!
(不过我都没想出来,去看题解,看不太懂还去问队友小哥的贪心。我巨菜蒟蒻还是要多练w)
}
在这题,为什么快?
一般的状压DP就是无头苍蝇,上走走下走走
而这里是有方向的,不是盲目搜索
其次它线性的原因是点对点的,就上面说的能不能有点对点的线性最短路方法w
但是方向是这里的灵魂
——从低处往高处走的方向
我们怎么判断方向
不禁让人想起了K短路的A*启发式算法(虽然那洛谷题我莫名wa了一下午很是郁闷qwq)
A*算法求路,是先终点为起点,倒边跑一次DJ,记下每一个点离终点的距离
再以这个距离加离起点距离为优先队列判断标准,进行DFS
之后跑过去就有方向了节省时间
跑K短就到终点的第K次就是了
5.(有想法未解决)是否可以自己想一个找方向的方法用A*算法优化旅行商问题?
A*是否有效,关键在于找方向的方法,找的越好,越快越准
比如直角坐标系下是x+y+z还是sqrt(x2+y2+z2)
但是旅行商问题,各状态都要有根据的话...
那要如同状压DP里,每个状态点的离结束的距离都要算出来吗
弄不好这个预处理时间花费是巨大的
连正规的TSP状压都有很多状态点能达不到,能忽略不看
然而经过多少点与现在在哪个位置,可能是必须要考虑的变量
所有就不知道怎么办
有点猴子打字的感觉哈哈哈
6.(未解决)智能算法如何找方向的?
不是我不会,而是我还没有来得及学,而且可能我学了也学不会,代码300行好长看懂好难哭了w
(我是电自专业的大一学生,编程是上个学期自学的C,就喜欢上了算法w。
不知道Pecco会不会嗷)
现在近似解决TSP的智能算法有遗传算法,蚁群算法和退火算法等
(目前还没看到A*算法)
我们ACM教练说:会更快,不一定是最优解
但是生活中很有用
所以我想去了解2333
但是肯定现在还和学姐没什么讨论的,
有点打扰学姐让学姐看了这么多w
————————我是分界线——————
oh,Pecco学姐
你也休息啦
Pecco的文字很有趣吸引人,也很深入浅出讲东西很明白wow
我挺想认识您,和您讨论问题,聊聊天的
QQ是3289630182,Pecco凭感觉叭
不是那种什么事都要无脑找别人帮忙的,单纯喜欢看Pecco的文字想认识Pecco,之前也这样认识了千千w(千千的博客太好看了https://www.dreamwings.cn/)
也不会没话找话或者消息发一大串的,我话多,但是意识到了都会克制自己w
期待一个新朋友w
以后想和Pecco多讨论一下算法
好优秀上进的学姐,棒~
