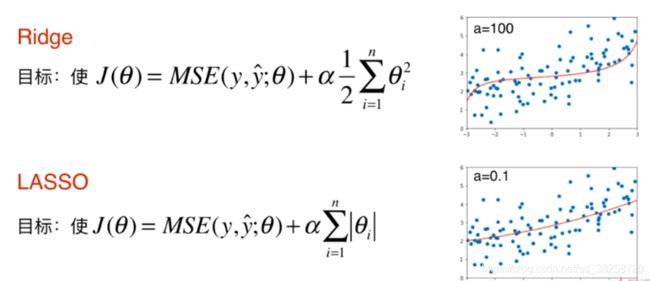机器学习入门(四)——多项式回归与模型泛化

一.多项式回归

测试的数据：

np.random.seed(666)
x = np.random.uniform(-3.0,3.0,size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)

简单线性回归的问题：

解决办法，增加一个特征：

X2 = np.hstack([X, X**2])

二.scikit-learn中的多项式回归于pipeline

关于关于PolynomialFeatures：

会产生10列数据。

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
 
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

from sklearn.metrics import mean_squared_error
 
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)
 
y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)

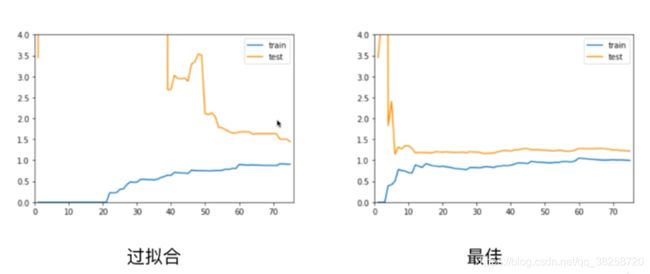
三.过拟合与欠拟合 Overfitting-and-Underfitting

欠拟合：

使用一次方程，则会出现欠拟合的现象，就是特征比较少，不能表示出数据的全部特征。

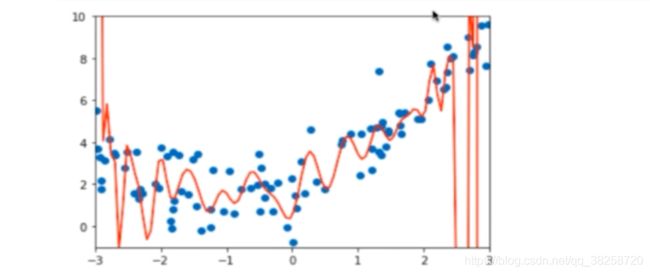
过拟合：
将PolynomialFeatures的参数调整到100，则会出现下面的情况：

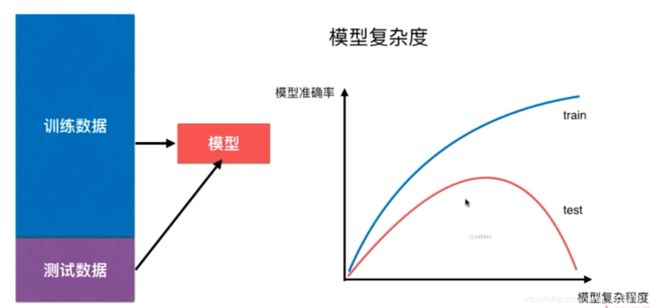
四.模型的泛化能力

泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力
这里使用测试数据集
机器学习主要解决的是过拟合的问题

PolynomialFeatures的参数为100
模型泛化能力太差，图中紫色的点过于偏离，会导致方差特别大

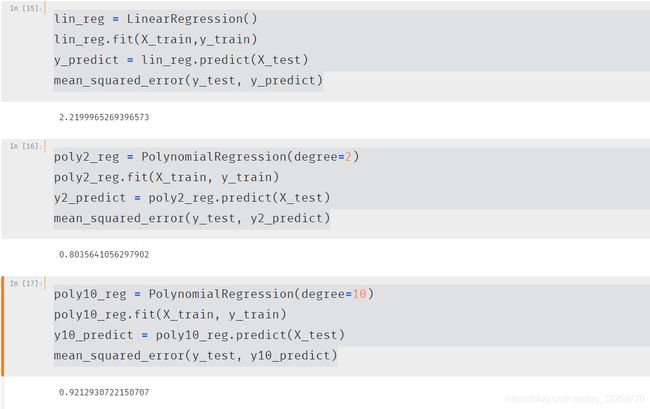
使用自身数据进行测试（分别为一次，二次，十次，100次）：




使用测试数据集查看泛化能力：

二阶的模型比一阶的模型泛化能力要强

10阶时变小，泛化能力下降了，100时就更明显了

上述两个测试能得出以下结论：

五.学习曲线

总共的训练数据集：
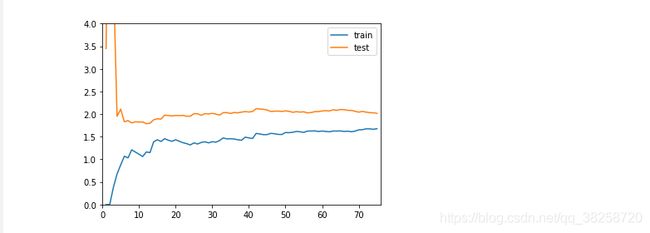
按训练集个数从1到75的学习曲线：

def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
    
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))
        
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(test_score), label="test")
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 4])
    plt.show()

一次线性回归：

from sklearn.linear_model import LinearRegression
plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test)

二次：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
 
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)

20次：

poly20_reg = PolynomialRegression(degree=20)
plot_learning_curve(poly20_reg, X_train, X_test, y_train, y_test)

得出的结论：
欠拟合训练和测试的整体误差都比较大

过拟合的训练集误差不大，但是测试误差比较大

六.验证数据集与交叉验证

由于训练数据集上误差很好，但测试上不好，所以将数据集分开
这样肯定比只用全为训练数据要好
有了模型后，通过测试数据上效率最好，调试参数，模型在围绕着测试数据集打转，有可能在测试数据集上过拟合

训练好后，模型给验证数据，找到验证数据的好参数模型
测试数据没有用过，完全不知的
这时的问题是随机，数据集的分割，如果有特殊的数据直接影响模型的结果
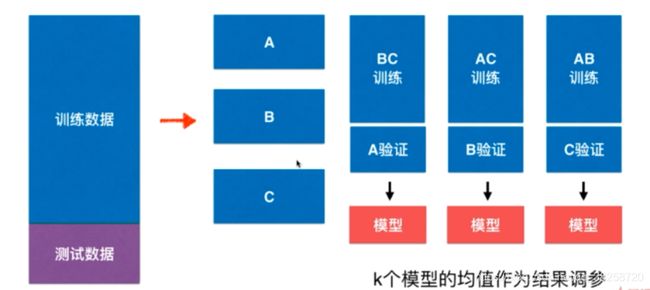
为了解决这个问题就是交叉验证
把数据分为k分，比如三分
每一个会有一个模型参数，求匀值

交叉验证

网格搜索默认就是交叉验证：

from sklearn.model_selection import GridSearchCV
param_grid = [
    {
     
        'weights': ['distance'],
        'n_neighbors': [i for i in range(2, 11)], 
        'p': [i for i in range(1, 6)]
    }
]
 
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)

缺点：每次训练K个模型，相当于整体性能慢了K倍

七.偏差方差平衡

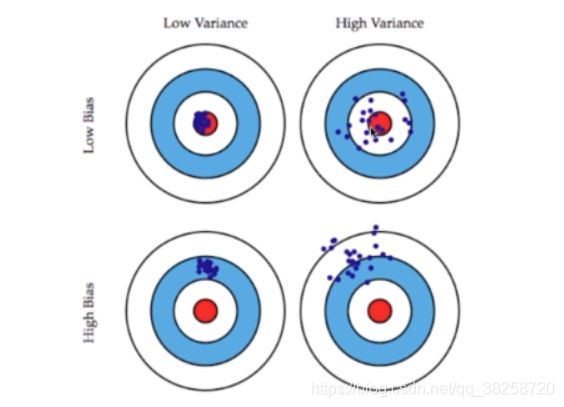
图二 偏差小，方差大
图三 偏差大，方差小
图四 偏差大，方差大

偏差：

方差：

knn对数据很敏感，一旦离它近的数据不合理或有问题则结果就不对，高度于依赖于样本数据
knn当使用所有样本时，即就是看哪个多就是哪个，则偏差最大，方差最小

机器学习的主要挑战，来自于方差，这是从算法的角度来说

八.模型泛化与岭回归 Model-Regularization-and-Ridge-Regression

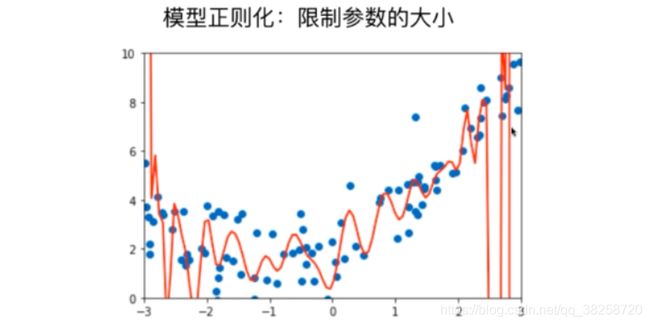多项式回归过拟合的情况，有一些系数会很大，模型正则化就是限制其不要太大

测试数据：

np.random.seed(42)
x = np.random.uniform(-3.0,3.0,size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + np.random.normal(0,1,size=100)

from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)

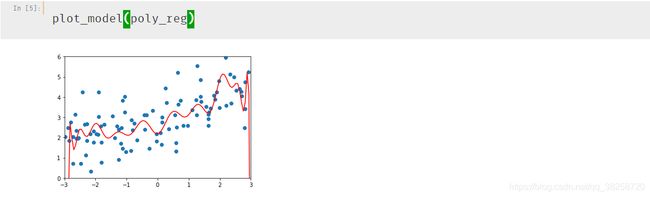
作图：

def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)
    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show() 

不使用岭回归

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

使用岭回归

from sklearn.linear_model import Ridge
 
def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])

九.LASSO

使用LASSO回归：

from sklearn.linear_model import Lasso
 
def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])

LASSO更倾向于直线，Ridge更倾向于曲线，

LASSO对应的theta有的为零，Selection Operator对应的特征无用

十.L1,L2和弹性网络

弹性网络：