金融过程的模拟（一）：CIR 过程的模拟
CIR过程（平方根扩散过程）是一类均值回归过程，它由Cox、Ingersoll和Ross（1985）提出，在金融中常用于建立短期利率或者波动性过程的模型。它的SDE公式如下：
其中，
代表t时刻的短期利率水平，k代表均值回归的速度( the speed of mean reversion), 
代表了长期均值水平（long-term mean），
恒定波动率(volatility)。
CIR过程相比于OU过程的一个好处是利率能保持非负(满足一定条件下，严格大于零)。
本文大致分为以下三个部分: 1. CIR过程的精确格式模拟；2. CIR的近似格式模拟；3.两种格式的比较。
1. CIR过程的精确模拟
CIR过程中的x_t的转移概率服从非中心化的卡方过程，所以CIR的精确离散化公式如下:
python代码如下：
def CIR_simulation_exact():
x = np.zeros((M+1,I))
x[0] = x0
for t in range(1, M+1):
df = 4 * theta * kappa / sigma ** 2
c = (sigma**2 * (1 - np.exp(-kappa*dt))) / (4 * kappa)
nc = np.exp(-kappa * dt) / c * x[t-1]
x[t] = c * npr.noncentral_chisquare(df, nc, size = I)
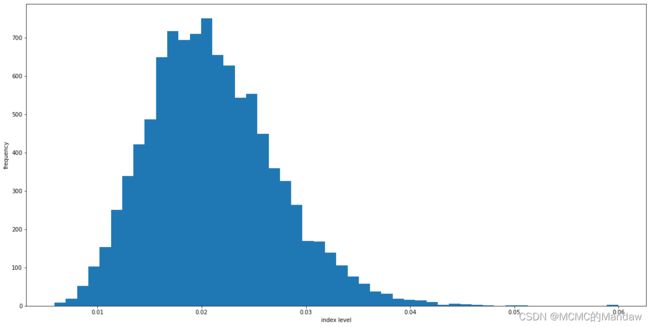
return x我们设置k=3,theta=0.02,sigma=0.1,X_0=0.04,T=1.0,dt=T/1000,产生了10000条模拟路径(后面实验的参数都一样),则在t=T时的直方图如下：
选取前10条路径如下：
综上，可以看出CIR呈现负的漂移(因为初值X_0=0.04>theta=0.02)，并均值复归于0.02。
2. CIR过程的近似模拟
我们采用欧拉离散化格式即
其中
服从相互独立的标准正态分布，且为保证非负，我们取
。
python代码如下:
def CIR_simulation_euler():
xh = np.zeros((M+1,I))
x = np.zeros_like(xh)
xh[0] = x0
x[0] = x0
for t in range(1, M+1):
xh[t] = (xh[t-1] +
kappa*(theta - np.maximum(xh[t-1],0))*dt +
sigma * np.sqrt(np.maximum(xh[t-1],0)) * math.sqrt(dt) * npr.standard_normal(I))
x = np.maximum(xh,0)
return x与1中相同，产生10000条模拟路径，结果如下：
从图上可以看出，近似模拟基本和精确模拟一致，生成的路径都是负漂移且收敛于0.02。
3. 精确模拟和近似模拟的比较
上面已经从直观上说明近似模拟能产生和精确模拟相似的结果，下面定量地比较两种模拟方式。
- 从主要地统计特征来看
比较两次产生地模拟路径在t=T时地主要统计量结果如下：
| STATISTIC | EXACT | EULER |
|---|---|---|
| size | 10000.000 | 10000.000 |
| min | 0.004 | 0.004 |
| max | 0.054 | 0.060 |
| mean | 0.021 | 0.021 |
| std | 0.006 | 0.006 |
| skew | 0.561 | 0.579 |
| kurtosis | 0.451 | 0.458 |
可以看出，近似地欧拉格式的模拟方法表现出了很好的统计属性。
- 从模拟地执行速度或时间来看
我们生成了100000条模拟路径，比较两种方法的执行速度，结果如下：
| EXACT | EULAR | |
| time | 6.66 s | 3.38 s |
可以看出，精确模拟的时间几乎时近似模拟的两倍，这主要是由于精确模拟中的非中心卡方分布采样的计算要求高于标准正态分布的采样。
综上，精确模拟需要花费近似模拟大概两倍的时间，而实际结果几乎一样。
参考教材
Simulation and Inference for Stochastic Differential Equations With R Examples.
Python for Finance，Second Edition.