Blog:https://www.jianshu.com/p/c4e24a6a9633 https://www.cnblogs.com/jingsupo/p/9865464.html
在用训练数据对模型进行拟合时会得到模型的一些参数,但将模型用于新数据时需重设这些参数,并且还需要评估这个模型的实用性。可以利用scikit-learn中的一些方法来达到这么目的。
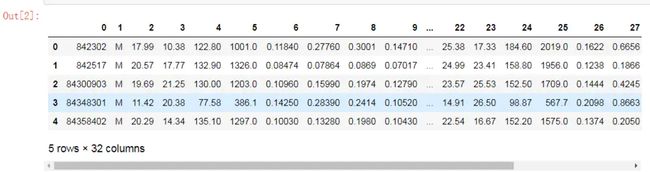
# 加载数据 - 威斯康星乳腺癌数据(利用pandas直接去UCI网站读取) import pandas as pd df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',header=None)
# 该数据有32列,第二列是关于样本的诊断结果(M代表恶性,B代表良性),第3列-32列包含了30个从细胞核照片中提取、用实数值标识的特征
# 观察缺失值,检查有没有缺失值 import missingno missingno.matrix(df)
# 对于分类模型来讲,目标变量值最好为数值,比如男为1,女为0。可以观察到该数据集的目标变量为M和B,要将其转化为0/1,而本例需要重点关注恶性的,所以要将M变为1,B变为0
# 先将数据分为特征列和目标列 X=df.loc[:,2:].values y=df.loc[:,1].values
from sklearn.preprocessing import LabelEncoder le = LabelEncoder() y=le.fit_transform(y)
# 被sklearn的LabelEncoder转换器转换之后,类标被存储在一个数组y中,此时M被标识为1,B为0。此时,可以通过transform方法来显示虚拟类标
# 将数据划分为训练集和测试集 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1)
1.基于流水线的工作流
在做数据处理时,需要用到不同的手法,如特征标准化,主成分分析,等等会重复用到某些参数,sklearn中提供了管道,可以一次性的解决该问题
通常处理:先用StandardScaler将数据标准化,然后做主成分分析降维(将数据集降维到二维空间),最后用逻辑回归做回归预测。
import pandas as pd from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.linear_model import LogisticRegression df = pd.read_csv('wdbc.csv') X = df.iloc[:, 2:].values y = df.iloc[:, 1].values # 标准化 sc = StandardScaler() X_train_std = sc.fit_transform(X_train) X_test_std = sc.transform(X_test) # 主成分分析PCA pca = PCA(n_components=2) X_train_pca = pca.fit_transform(X_train_std) X_test_pca = pca.transform(X_test_std) # 逻辑斯蒂回归预测 lr = LogisticRegression(random_state=1) lr.fit(X_train_pca, y_train) y_pred = lr.predict(X_test_pca)
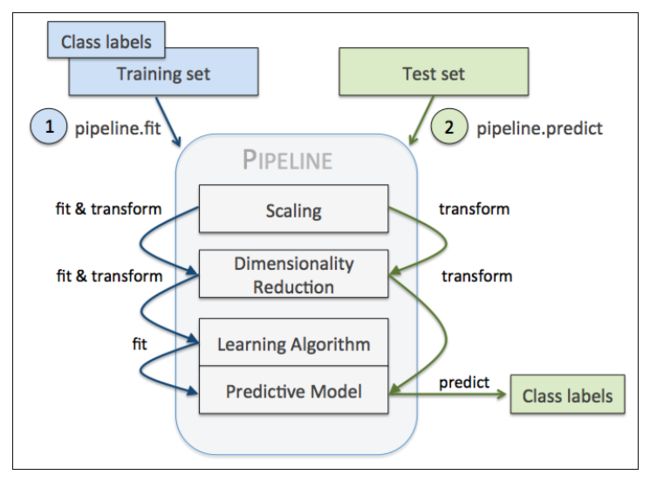
管道处理:可以利用Pipeline类来进行工作流:Pipeline对象采用元组构成的序列作为输入,其中每个元组中的第一个值为一个字符串,可以是任意的标识符,作为变量名,通过它来访问流水线中的元素,而元组的第二个值则为scikit-learn中的一个转换器Transformer或者评估器Estimator,管道中间每一步由sklearn中的Transformer构成,最后一步是一个Estimator。
from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.linear_model import LogisticRegression from sklearn.pipeline import Pipeline pipe_lr = Pipeline([('scl',StandardScaler()),('pca',PCA(n_components=2)),('clf',LogisticRegression(random_state=1))]) pipe_lr.fit(X_train,y_train) print("Test Accuracy:%.3f"%pipe_lr.score(X_test,y_test))
Out:Test Accuracy: 0.947
本例中,管道包含两个中间步骤,一个StandardScaler和一个PCA,这俩都是Transformer,逻辑斯蒂回归分类器是Estimator。
当管道pipe_lr执行fit方法时,首先StandardScaler执行fit和transform方法,然后将转换后的数据输入给PCA,PCA同样执行fit和transform方法,最后将数据输入给LogisticRegression,训练一个LR模型。
对于管道来说,中间有多少个transformer都可以,其工作方式如下:
另外,使用管道能减少很多代码量。
2.使用交叉验证评估模型性能
训练机器学习模型的关键一步是要评估模型的泛化能力。如果训练好模型后,还是用训练集测评估模型的性能,显然不符合逻辑。一个模型如果性能不好,要么是因为模型过于复杂导致过拟合(高方差),要么是模型过于简单导致导致欠拟合(高偏差)。
如果一个模型过于简单,可能会面临欠拟合(高偏差)问题,但是如果模型太过复杂,又会面临过拟合(高方差)问题。所以必须要借助一些手段对模型进行评估。
评价模型的性能方法(泛化性能),主要有两种交叉验证计数:Holdout交叉验证和K折交叉验证。其中最常用的就是K折交叉验证,该方法鲁棒性好。可以比较好的应对噪声等问题。
2.1 Holdout交叉验证
Holdout方法很简单,就是将数据集分为训练集和测试集,前者用于训练,后者用于评估
如果在模型选择的过程中,始终用测试集来评价模型性能,这实际上也将测试集变相地转为了训练集,这时候选择的最优模型很可能是过拟合的。
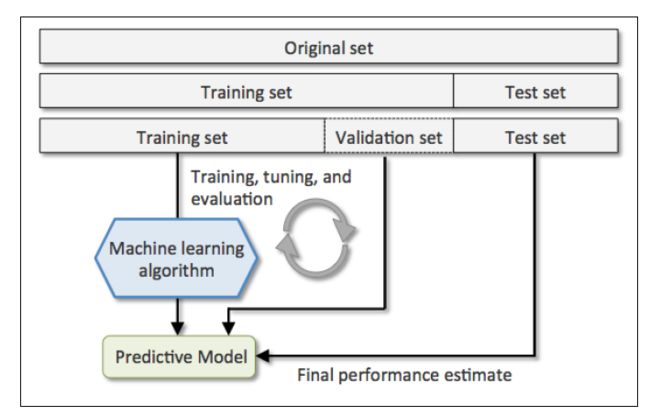
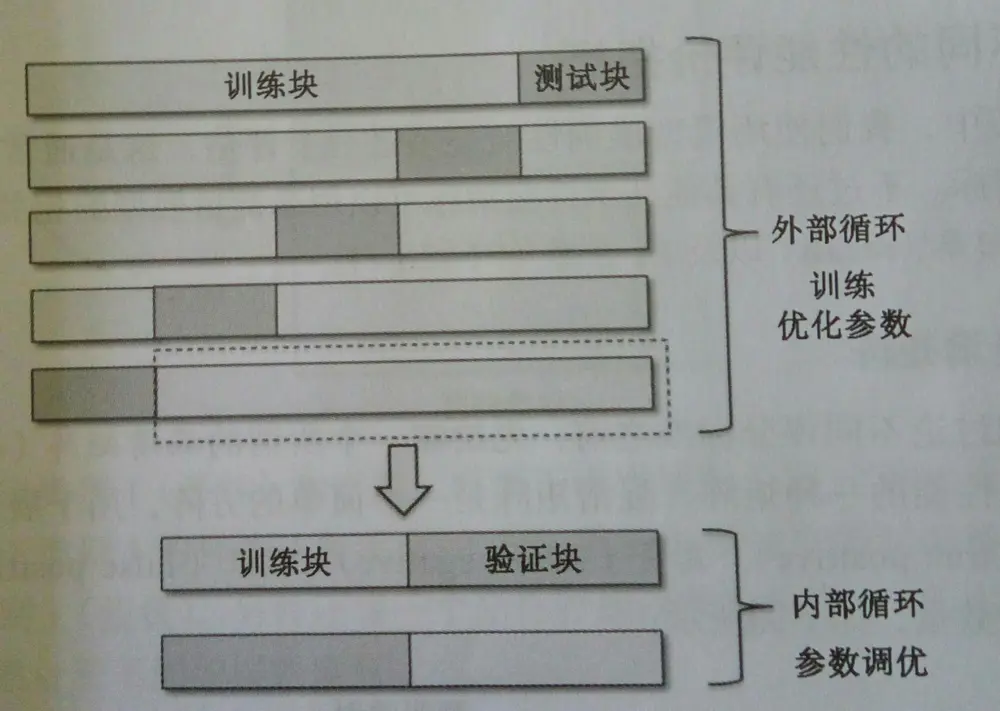
更好的Holdout方法是将原始训练集分为三部分:训练集、验证集和测试集。训练集用于训练不同的模型,验证集用于模型选择。而测试集由于在训练模型和模型选择这两步都没有用到,对于模型来说是未知数据,因此可以用于评估模型的泛化能力。下图展示了Holdout方法的步骤:
缺点:它对数据分割的方式很敏感,如果原始数据集分割不当,这包括训练集、验证集和测试集的样本数比例,以及分割后数据的分布情况是否和原始数据集分布情况相同等等。所以,不同的分割方式可能得到不同的最优模型参数
2.2 K折交叉验证
K折交叉验证的过程,第一步使用不重复抽样将原始数据随机分为k份,第二步 k-1份数据用于模型训练,剩下那一份数据用于测试模型。然后重复第二步k次,就得到了k个模型和他的评估结果为了减小由于数据分割引入的误差,通常k折交叉验证要随机使用不同的划分方法重复p次,常见的有10次10折交叉验证),然后计算k折交叉验证结果的平均值作为参数/模型的性能评估。使用k折交叉验证来寻找最优参数要比holdout方法更稳定。一旦找到最优参数,要使用这组参数在原始数据集上训练模型作为最终的模型。
K折交叉验证原理:不重复地随机将训练数据集划分为K个,其中K-1个用于模型的训练,剩余的1个用于测试。重复此过程K次,就可以得到K个模型对模型性能的评价。
K折交叉验证使用不重复采样,优点是每个样本只会在训练集或测试中出现一次,这样得到的模型评估结果有更低的泛化。
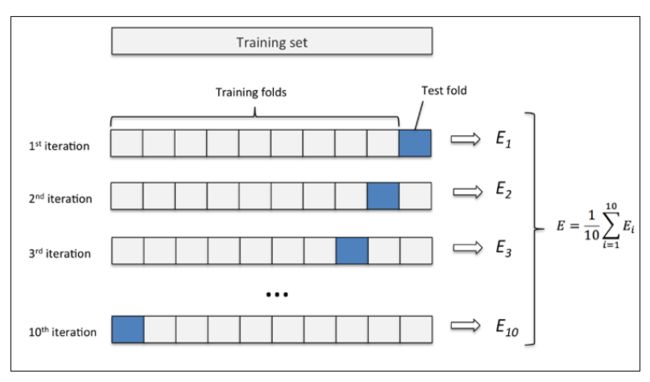
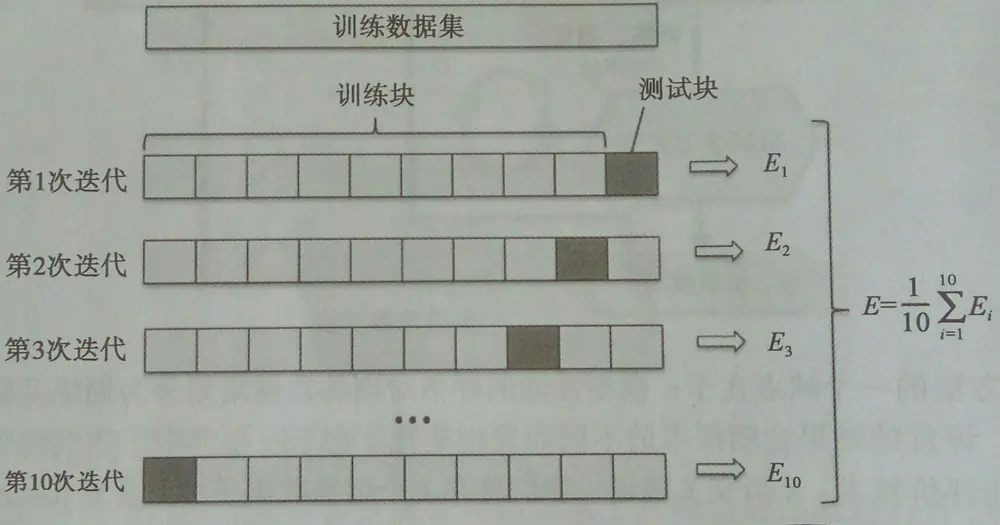
下图演示了10折交叉验证:
10次10折交叉验证,是将按十种划分方法,每次将数据随机分成k分,k-1份训练,k份测试。获取十个模型和评估结果,然后取10次的平均值作为性能评估:
from sklearn.model_selection import StratifiedKFold pipe_lr = Pipeline([('sc', StandardScaler()), ('pca', PCA(n_components=2)), ('lr', LogisticRegression(random_state=1))]) pipe_lr.fit(X_train, y_train) kfold = StratifiedKFold(y=y_train, n_folds=10, random_state=1) scores= [] for k, (train, test) in enumerate(kfold): pipe_lr.fit(X_train[train], y_train[train]) score = pipe_lr.score(X_train[test], y_train[test]) scores.append(scores) print('Fold: %s, Class dist.: %s, Acc: %.3f' %(k+1, np.bincount(y_train[train]), score))print('CV accuracy: %.3f +/- %.3f' %(np.mean(scores), np.std(scores)))
K折交叉验证使用无重复抽样技术,通常情况下,将K折交叉验证用于模型的调优,也就是找到使得模型泛化性能最优的超参值。一旦找到了满意的超参值,就可以在全部的训练集上重新训练模型,并使用独立的测试集对模型性能做出最终评价。K折交叉验证中K的值一般是10,对于大多数数据来说是比较合理的。但是如果数据集比较小,建议加大K值。这可以使模型评价时得到较小的偏差(不怎么会欠拟合),但是方差会变大(过拟合)。当数据集非常小时,建议用留一交叉验证。留一交叉验证是将数据集划分的数量等同于样本量(K=n),这样每次只有一个样本用于测试。如果数据集较大,可以减少K值。在scikit-learn中可以用KFold来进行k折交叉验证。但是当类别比例相差较大时,建议用分层交叉验证。在分层交叉验证中,类别比例在每个分块中得以保持,这使得每个分块中的类别比例与训练集的整体比例一致。
# 分层K折交叉验证
# 当我们使用kfold迭代器在k个块中进行循环时,使用train中返回的索引去拟合逻辑斯底回归流水线。通过流水线,我们可以保证
# 每次迭代时样本都得到标准化缩放,然后使用test索引计算模型的准确性和f1值,并存放到两个列表中,用于计算平均值和标准差
import numpy as np
from sklearn.model_selection import StratifiedKFold
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler from sklearn.metrics import f1_score pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(random_state=1))]) kfold = StratifiedKFold(n_splits=10,random_state=1) # 通过n_splits来设置块的数量 scores=[] f1_scores=[] for k,(train,test) in enumerate(kfold.split(X_train,y_train)): pipe_lr.fit(X_train[train],y_train[train]) p_pred = pipe_lr.predict(X_train[test]) f1_sc = f1_score(y_true=y_train[test],y_pred=p_pred) f1_scores.append(f1_sc) score=pipe_lr.score(X_train[test],y_train[test]) scores.append(score) print('Fold: %s, Class dist.: %s,Acc: %.3f,f1 score:%.3f' %(k+1,np.bincount(y_train[train]),score,f1_sc))
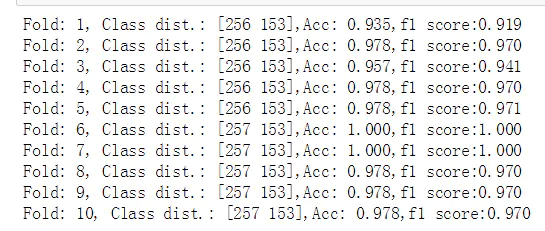
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores),np.std(scores)))
print("CV f1 score:%.3f +/- %.3f" % (np.mean(f1_scores),np.std(f1_scores)))
也可以使用sklearn中的cross_val_score直接将上述结果计算出来,方法更简便
- cross_val_score中scoring参数取值有:Valid options are ['accuracy', 'adjusted_mutual_info_score', 'adjusted_rand_score', 'average_precision', 'completeness_score', 'explained_variance', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'fowlkes_mallows_score', 'homogeneity_score', 'mutual_info_score', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_squared_error', 'neg_mean_squared_log_error', 'neg_median_absolute_error', 'normalized_mutual_info_score', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc', 'v_measure_score']
from sklearn.model_selection import StratifiedKFold pipe_lr = Pipeline([('sc', StandardScaler()), ('pca', PCA(n_components=2)), ('lr', LogisticRegression(random_state=1))]) pipe_lr.fit(X_train, y_train) scores = cross_val_score(estimator=pipe_lr, X=X_train, y=y_train, cv=10, n_jobs=1) print('CV accuracy scores: %s' %scores) # CV即K print('CV accuracy: %.3f +/- %.3f' %(np.mean(scores), np.std(scores)))
# sklearn方法求k折交叉验证 # cross_val_score可以将不同分块的性能评估分布到多个CPU上处理 # 如果将n_jobs参数设置为1,则与StratifiedKFold一样 # 只使用一个CPU对性能进行评估,如果设置为-1,则可利用计算机所有的CPU并行地进行计算 # 还可通过scoring参数来计算不同的评估指标 from sklearn.model_selection import cross_val_score scores=cross_val_score(estimator=pipe_lr, X=X_train, y=y_train, scoring="accuracy", cv=10, n_jobs=1) print("CV accuracy scores: %s" % scores)
print('CV accurary:%.3f +/- %.3f' % (np.mean(scores),np.std(scores)))计算f1值
from sklearn.model_selection import cross_val_score f1_scores = cross_val_score(estimator=pipe_lr,X=X_train,y=y_train,scoring='f1',cv=10,n_jobs=-1) print('CV f1 scores:%s'%f1_scores)
计算auc值
from sklearn.model_selection import cross_val_score aucs = cross_val_score(estimator=pipe_lr,X=X_train,y=y_train,scoring='roc_auc',cv=10,n_jobs=-1) print('CV auc scores:%s'%aucs)
3.通过学习及验证曲线来调试算法
3.1 通过学习曲线,可以判定算法偏差和方差问题
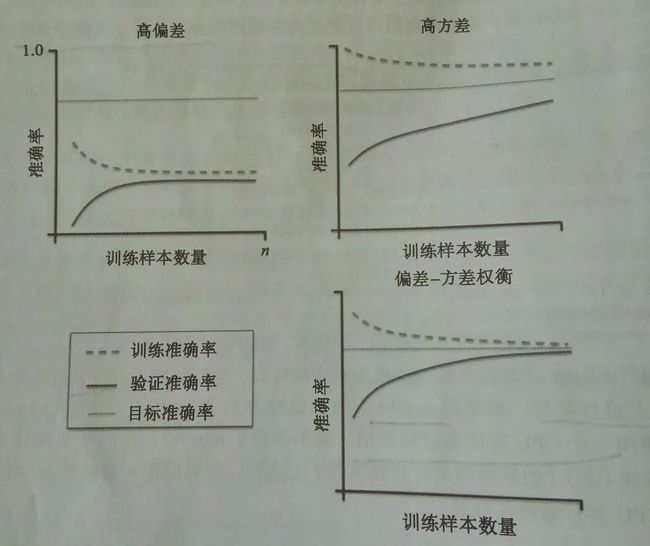
将模型的训练及准确性验证看做是训练数据集大小的函数,并绘制图像,可以比较容易的看出模型是高偏差还是高方差的问题,以及收集更多的数据是否有助于解决问题
例如训练Logistic回归分类器时,在该分类器中,可以调整的超参有:
- penalty:正则惩罚项,可以选L1或者L2.默认是L2
- C:正则化倒数,C越小,代表正则化程度越高
- solver:有四个值可选:'netton-cg','lbfgs',liblinear','sag'.默认是liblinear,该方法对数据量小的数据效果较好,且只能处理两分类。sag在数据量比较大的时候速度 较快。面对多分类的话,除了liblinear之外其他都可以,且另外几个只能支持L2惩罚项
高方差:右上子图一是个高方差模型,训练准确率和交叉验证准确率之间有很大差距。
解决:收集更多的训练数据(降低模型过拟合的概率)或者降低模型的复杂度,比如增加正则化程度,降低特征的数量等。对于不适合正则化的模型,可以通过特征选择或者特征提取降低特征的数量。
import matplotlib.pyplot as plt import numpy as np %matplotlib inline from sklearn.model_selection import learning_curve from sklearn.pipeline import Pipeline from sklearn.linear_model import LogisticRegression from sklearn.preprocessing import StandardScaler pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(penalty='l2',random_state=0))]) train_sizes,train_scores,test_scores = learning_curve(estimator=pipe_lr,X=X_train,y=y_train,train_sizes = np.linspace(0.1,1.0,10),cv=10,n_jobs=-1)
# learning_curve中的train_sizes参数控制产生学习曲线的训练样本的绝对/相对数量,此处设置的train_sizes=np.linspace(0.1, 1.0, 10),将训练集大小划分为10个相等的区间
# learning_curve默认使用分层k折交叉验证计算交叉验证的准确率,通过cv设置k train_mean = np.mean(train_scores,axis=1) train_std = np.std(train_scores,axis=1) test_mean = np.mean(test_scores,axis=1) test_std = np.std(test_scores,axis=1) plt.plot(train_sizes,train_mean,color='blue',marker='o',markersize=5,label='training accuracy') plt.fill_between(train_sizes,train_mean+train_std,train_mean-train_std,alpha=0.15,color='blue') plt.plot(train_sizes,test_mean,color='green',linestyle='--',markersize=5,label='validation accuracy') plt.fill_between(train_sizes,test_mean+test_std,test_mean-test_std,color='green',alpha=0.15) plt.grid() plt.xlabel('Number of training samples') plt.ylabel('Accuracy') plt.legend(loc='best/lower right') plt.ylim([0.8,1.0])
plt.show()
通过上面的代码,可以得到下面的学习曲线:
3.2 通过验证曲线,可以判定算法欠拟合和过拟合问题
验证曲线和学习曲线相似,不过绘制的不是样本大小和训练准确率、测试准确率之间的函数关系,而是准确率与模型参数之间的关系
from sklearn.model_selection import validation_curve param_range = [0.001,0.01,0.1,1.0,10.0,100.0] pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(penalty='l2',random_state=0))]) train_scores,test_scores = validation_curve(estimator=pipe_lr,X=X_train,y=y_train, param_name='clf__C', param_range=param_range, cv=10) train_mean = np.mean(train_scores,axis=1) train_std = np.std(train_scores,axis=1) test_mean = np.mean(test_scores,axis=1) test_std = np.std(test_scores,axis=1) plt.plot(param_range,train_mean,color='blue',marker='o',markersize=5,label='training accuracy') plt.fill_between(param_range,train_mean+train_std,train_mean-train_std,color='blue',alpha=0.15) plt.plot(param_range,test_mean,color='green',linestyle='--',markersize=5,label='validation accuracy') plt.fill_between(param_range,test_mean+test_std,test_mean-test_std,color='green',alpha=0.15) plt.grid() plt.xscale('log') #设置X轴的缩放比例,可以用'log','linear','logit','symlog' plt.legend(loc='best') plt.xlabel('Parameter C') plt.ylabel('Accuracy') plt.ylim([0.8,1])
plt.show()
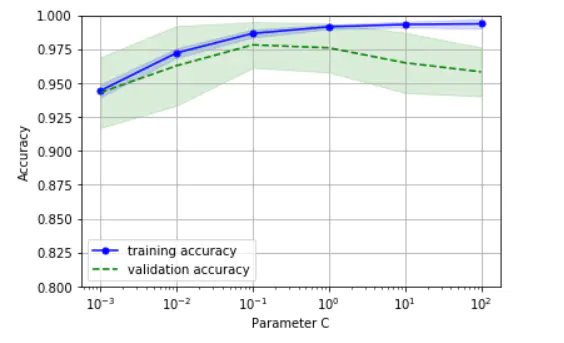
通过上面的代码,可以得到参数C的验证曲线:
总之,可以使用学习曲线判断算法是否拟合程度(欠拟合或者过拟合),然后使用验证曲线评估参数获取最好的参数。
4.使用网络搜索来调试算法/调优模型
在机器学习中,有两类参数:一是通过训练数据学习得到的参数,如Logistic回归中的回归/权重系数;二是算法中需要单独进行优化的参数,即调优参数,也称超参(模型的超参数,也就是需要人工设定的参数),如逻辑回归中的正则化系数、决策树中的深度系数。
权重参数可以通过验证曲线来获取最好的参数,而超参数则可以使用网格搜索调参
前面是通过验证曲线来得到较优的C值,但是通过图形来得出最优值会带点主观性,所以可以利用网格搜索,通过明确的结果寻找最优的超参值的组合
网格搜索其实就是暴力搜索,事先为每个参数设定一组值,然后穷举各种参数组合,找到最好的那组
from sklearn.model_selection import GridSearchCV pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(random_state=0))]) param_range=[0.0001,0.001,0.01,0.1,1,10,100,1000] param_penalty=['l1','l2'] param_grid=[{ 'clf__C':param_range,'clf__penalty':param_penalty}] # param_grid = [{'clf__C': param_range, 'clf__kernel': ['linear']}, {'clf__C': param_range, 'clf__gamma': param_range, 'clf__kernel': ['rbf']}]
gs = GridSearchCV(estimator=pipe_lr,param_grid=param_grid,scoring='f1',cv=10,n_jobs=-1)
gs = gs.fit(X_train,y_train)
print(gs.best_score_)
print(gs.best_params_)
# 参数选择结果 0.970063106828 { 'clf__C': 0.1, 'clf__penalty': 'l2'}
可以看到C值和penalty的最优组合是0.1和l2。
上述代码是在流水线中调优的,GridSearchCV中param_grid参数是字典构成的列表,所以在GridSearchCV的param_grid参数以字典的方式定义待调优的参数时,填写的是clf__C(英文状态下两个下划线)和clf__penalty,这个clf在流水线中代表定义的逻辑回归,后面代表的是要调优的参数。(对于线性SVM,我们只评估参数C;对于RBF核SVM,我们评估C和gamma。)
在训练数据集上完成网格搜索后,可以通过best_score_属性得到你在scoring参数中指定的指标的最优值,而具体的待调优的参数信息可通过best_params_属性得到,即通过best_parmas_得到最优参数组合
最后可以通过GridSearchCV对象的best_estimator_属性对最优模型进行性能评估:
from sklearn.metrics import f1_score
# 直接利用最优参数建模 clf = gs.best_estimator_ clf.fit(X_train,y_train) y_pred = clf.predict(X_test) print('Test f1 score:%.3f' % f1_score(y_true=y_test,y_pred=y_pred))
Test f1 score:0.963
也可以:
from sklearn.model_selection import cross_val_score clf=gs.best_estimator_ clf.fit(X_train,y_train) f1_scores = cross_val_score(estimator=clf,X=X,y=y,scoring='f1',cv=10,n_jobs=-1) print("CV f1 score:%.3f" % np.mean(f1_scores))
clf = gs.best_estimator_ clf.fit(X_train, y_train) print('Test accuracy: %.3f' %clf.score(X_test, y_test))
网格搜索虽然很给力,但是穷举过于耗时,计算速度不怎么好。因为它通过对指定的不同超参列表进行暴力穷举搜索,并计算评估每个组合对模型性能的影响,以获得参数的最优组合在sklearn中
sklearn中还实现了随机搜索,使用RandomizedSearchCV类,随机采样出不同的参数组合。其他方法参考:http://scikit-learn.org/stable/modules/grid_search.html#exhaustive-grid-search
5.通过嵌套交叉验证来选择算法
结合k折交叉验证和网格搜索是调参的好手段。可是如果需要考虑选择最合适的算法,一般采用嵌套交叉验证方法。
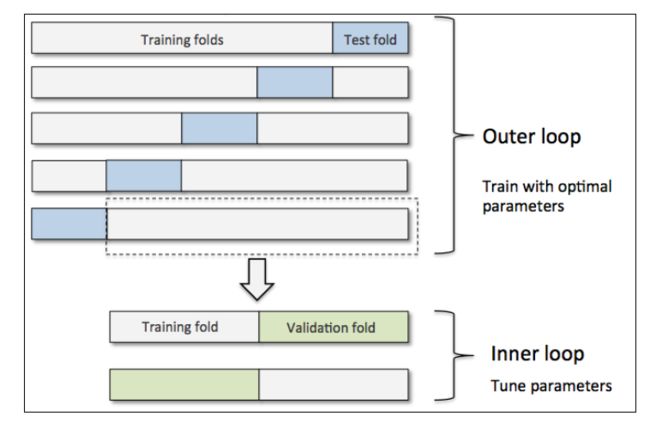
嵌套交叉验证外层有一个k折交叉验证将数据分为训练集和测试集。还有一个内部交叉验证用于选择模型算法。下图演示了一个5折外层交叉沿则和2折内部交叉验证组成的嵌套交叉验证,也被称为5*2交叉验证:
sklearn使用嵌套交叉验证:
# svc的精确度 gs = GridSearchCV(estimator=pipe_svc, param_grid=param_grid, scoring='accuracy', cv=10, n_jobs=-1) scores = cross_val_score(gs, X, y, scoring='accuracy', cv=5) print('CV accuracy: %.3f +/- %.3f' %(np.mean(scores), np.std(scores)))
# 决策树分类器精确度 gs = GridSearchCV(estimator=DecisionTreeClassifier(random_state=0), param_grid=[{ 'max_depth': [1,2,3,4,5,6,7, None]}], scoring='accuracy', cv=5) scores = cross_val_score(gs, X_train, y_train, scoring='accuracy', cv=5) print('CV accuracy: %.3f +/- %.3f' %(np.mean(scores), np.std(scores)))
# 比较下两者的精确度,即可知道那种算法更加合适
本例使用逻辑回归和随机森林来对这个数据集进行嵌套交叉验证:
# 逻辑回归 from sklearn.model_selection import cross_val_score,GridSearchCV from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(random_state=0))]) param_range=[0.0001,0.001,0.01,0.1,1,10,100,1000] param_penalty=['l1','l2'] param_grid = [{ 'clf__C':param_range,'clf__penalty':param_penalty}] clf_gs = GridSearchCV(estimator=pipe_lr,param_grid=param_grid,scoring='f1',cv=10,n_jobs=-1) clf_f1_scores = cross_val_score(estimator=clf_gs,X=X,y=y,scoring='f1',cv=5) print('CV clf f1 score:%.3f +/- %.3f'%(np.mean(clf_f1_scores),np.std(clf_f1_scores)))
CV clf f1 score:0.969 +/- 0.012
# 随机森林 from sklearn.ensemble import RandomForestClassifier rfc = RandomForestClassifier(random_state=0) #在bootstap为True和False的情况下的参数组合 rfc_grid=[{ 'n_estimators':[3,10,15],'max_depth':[1,2,3,4,5,6,7,None]}, { 'bootstrap':[False],'n_estimators':[3,10],'max_depth':[1,2,3,4,5,6,7,None]}] rfc_gs = GridSearchCV(estimator=rfc,param_grid=rfc_grid,cv=10,scoring='f1',n_jobs=-1) rfc_f1_scores = cross_val_score(estimator=rfc_gs,X=X,y=y,scoring='f1',cv=5) print('CV clf f1 score:%.3f +/- %.3f'%(np.mean(rfc_f1_scores),np.std(rfc_f1_scores)))
CV clf f1 score:0.948 +/- 0.023
从结果来看,逻辑回归的效果似乎更好,随机森林可以视为多颗决策树的集成,鲁棒性更强,泛化能力更好,不易产生过拟合现象。但是噪声比较大的情况下会过拟合。可以简单的将随机森林算法概括为四个简单步骤:
1.使用bootstrap抽样方法随机选择N个样本用于训练(从训练集中随机可重复地选择N个样本)
2.使用第1步选定的样本来构造一个决策树。节点划分规则如下:
(1)不重复地随机选择d个特征
(2)根据目标函数的要求,如最大化信息增益,使用选定的特征对节点进行划分
3.重复上述过程1~2000次
4.汇总每棵树的类标进行多数投票。比如对于二分类类标,总共有15棵树,有10棵树分为1,5棵树分为0,则多数服从少数,最终结果为1
随机森林相对于决策树来讲没有那么好的可解释性,但其显著优势在于不必担心超参值的选择。不需要对随机森林进行剪枝,因为相对于单棵决策树来讲,集成模型对噪声的鲁棒性更好
在实践中,真正需要关心的参数是为构建随机森林所需的决策树数量。通常情况下,决策树的数量越多,随机森林整体的分类表现越好,但这会增加计算成本。其他可调的参数有:
1.n_estimators : 随机森林中树的数量,也就是弱分类器的数量
2.criterion: 两种衡量分割效果的方法,有基尼系数法和熵法(entropy)。
3.max_features: 寻找最佳分割时要考虑特征变量的个数
4.max_depth: 设置决策树最大深度,如果不设置该变量,决策树一直延伸直至每个叶节点都完美分类,或者所有叶节点内数量达到min_samples_split指定的样本数量。
5.min_samples_split: 分割一个内部节点所要求的最低样本含量,低于这个数量就不再分割了。
6.max_leaf_nodes : 叶节点最大数目,默认不限制叶节点的最大数量。
7.min_impurity_split: 如果纯度还高于阈值,继续分割,如果达到阈值,成为叶节点。
8.bootstrap : 在生长树的时候是否采用bootstrap的方法,默认是是True
6.不同的性能评价指标
理论:https://www.jianshu.com/p/9fd57e9c85f5
6.1 混淆矩阵
除了准确率,还有不少评价指标,如查准率,查全率,F1值等
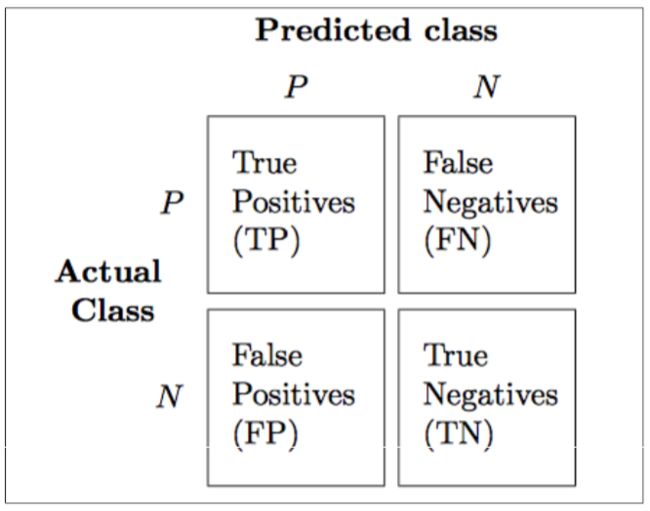
混淆矩阵(confusion matrix),能够展示学习算法表现的矩阵。混淆矩阵是一个平方矩阵,其中记录了一个分类器的TP(true positive)、TN(true negative)、FP(false positive)和FN(false negative):
# Python实现混淆矩阵(2*2矩阵) from sklearn import metrics metrics.calinski_harabaz_score(input, y_pred)
- TP实际为真,判断成功(判断为真)的个数
- FN实际为真,判断错误(判断为假)
- FP实际为假,判断错误(判断为真)
- TN实际为假,判断成功(判断为假)
# 先利用网格搜索算出最优的参数 from sklearn.metrics import confusion_matrix,classification_report from sklearn.linear_model import LogisticRegression from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.model_selection import GridSearchCV pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(random_state=0))]) param_range = [0.00001,0.0001,0.001,0.01,0.1,1,10,100,1000] param_penalty = ['l1','l2'] param_grid=[{ 'clf__C':param_range,'clf__penalty':param_penalty}] clf_gs = GridSearchCV(estimator=pipe_lr,param_grid=param_grid,scoring='f1',cv=10,n_jobs=-1) gs = clf_gs.fit(X_train,y_train) print(gs.best_params_)
# 结果为: { 'clf__C': 0.1, 'clf__penalty': 'l2'}
clf = clf_gs.best_estimator_ clf.fit(X_train,y_train) y_pred = clf.predict(X_test) confmat=confusion_matrix(y_true=y_test,y_pred=y_pred) class_report = classification_report(y_true=y_test,y_pred=y_pred) print(confmat) print('******************************') print(class_report) # 显示混淆矩阵
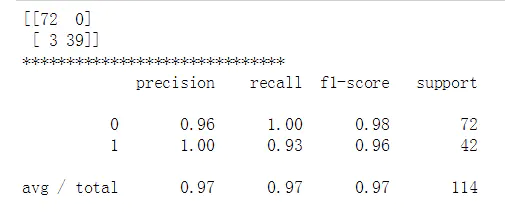
# 可视化混淆矩阵 fig,ax=plt.subplots(figsize=(2.5,2.5)) ax.matshow(confmat,cmap=plt.cm.Blues,alpha=0.3) for i in range(confmat.shape[0]): for j in range(confmat.shape[1]): ax.text(x=j,y=i,s=confmat[i,j],va='center',ha='center') plt.xlabel('predicted label') plt.ylabel('true label')
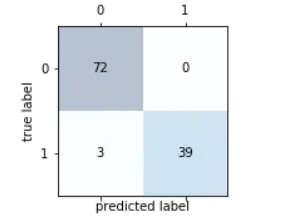
6.2 精度和召回率
from sklearn.metrics import precision_score #精度 from sklearn.metrics import recall_score,f1_score #召回率,f1分数 print('Precision:%.3f'%precision_score(y_true=y_test,y_pred=y_pred)) print('Recall:%.3f'%recall_score(y_true=y_test,y_pred=y_pred)) print('f1:%.3f'%f1_score(y_true=y_test,y_pred=y_pred))
Precision:1.000 Recall:0.929 f1:0.963
# 因为scikit-learn中将正类类标标识为1,如果想指定一个不同的正类类标来评分的话,可以如下操作 from sklearn.metrics import make_scorer,f1_score scorer = make_scorer(f1_score,pos_label=0) gs = GridSearchCV(estimator=pipe_svc,param_grid=param_grid,scoring=scorer,cv=10)
以上这些也可以通过cross_val_score中的scoring参数指定计算出来
6.3 ROC曲线
from sklearn.metrics import roc_curve,auc from scipy import interp X_train2=X_train[:,[4,14]] cv = StratifiedKFold(y_train,n_folds=3,random_state=1) fig=plt.figure(figsize=(7,5)) mean_tpr = 0.0 mean_fpr = np.linspace(0,1,100) all_tpr=[] for i,(train,test) in enumerate(cv): probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test]) fpr,tpr,thresholds = roc_curve(y_train[test],probas[:,1],pos_label=1) mean_tpr+=interp(mean_fpr,fpr,tpr) mean_tpr[0]=0.0 roc_auc=auc(fpr,tpr) plt.plot(fpr,tpr,lw=1,label='ROC fold %d (area=%0.2f)'%(i+1,roc_auc)) plt.plot([0,1],[0,1],linestyle='--',color=(0.6,0.6,0.6),label='random guessing') mean_tpr/=len(cv) mean_tpr[-1]=1.0 mean_auc=auc(mean_fpr,mean_tpr) plt.plot(mean_fpr,mean_tpr,'k--',label='mean ROC(area=%0.2f)'%mean_auc,lw=2) plt.plot([0,0,1],[0,1,1],lw=2,linestyle=':',color="black",label='perfect performance') plt.xlim([-0.05,1.05]) plt.ylim([-0.05,1.05]) plt.xlabel('false positive tate') plt.ylabel('true positive rate') plt.title('Receiver Operator Characteristic') plt.legend(loc='best') plt.show()