【机器学习】简介+Scikit-Learn介绍+超参数和模型验证+特征工程

机器学习方法应用在数据科学领域，把他看作是一种数学建模更合适。
机器学习本质就是借助数学模型理解数据。给模型装上可以适应观测数据的可调参数时，学习就开始了。此时程序就具有从数据中学习的能力。一旦模型可以你和旧的观测数据，那么它们就可以预测并解释新的观测数据

5.1 机器学习简介

一、机器学习的分类

• 有监督学习：指对数据的若干特征与若干标签（类型）之间的关联性进行建模的过程
  • 分类classification
  • 回归regression
• 无监督学习：指对不带任何标签的数据特征进行建模
  • 聚类dementionality reduction
  • 降维clustring
• 半监督学习

二、机器学习应用的定性示例

附录（https://github.com/jakevdp/PythonDataScienceHandbook）

1. 分类： 预测离散标签

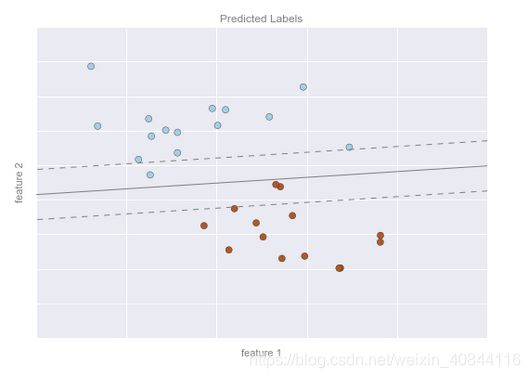
“分类”指的是数据具有离散的类型标签。

我们看到的是二维数据，也就是说每个数据点都有两个特征
数据点还用一种颜色表示一个类型标签
假设平面上有一条可以将两种类型分开的直线，直线的两侧分别是一种类型:
我们的模型其实就是“一条可以分类的直线”，而模型参数其实就是直线位置与方向的数值;
这些模型参数的最优解都可以通过学习数据获得（也就是机器学习的“学习”），这个过程通常被称为训练模型。
模型现在已经训练好了，可以对一个新的、不带标签的数据进行分类，也就是说，拿一组新数据，根据这个模型为新数据分配标签，这个阶段通常被称为预测
一些重要的分类算法，包括高斯朴素贝叶斯分类、支持向量机，以及随机森林分类。

2. 回归： 预测连续标签

回归任务与离散标签分类算法相反，其标签是连续值。

有一个二维数据，每个数据点有两个特征。
数据点的颜色表示每个点的连续标签。
用简单线性回归模型作出假设，如果我们把标签看成是第三个维度，那么就可以将数据拟合成一个平面方程——这就是著名的在二维平面上线性拟合问题的高阶情形。

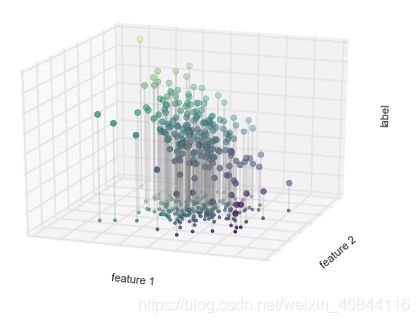
一些重要的回归算法，包括线性回归、支持向量机，以及随机森林回归

3. 聚类： 为无标签数据添加标签

数据被聚类算法自动分成若干离散的组别。
一个聚类模型会根据输入数据的固有结构判断数据点之间的相关性。
通过最快、最直观的 k-means 聚类算法，就可以发现如图所示的类簇。

k-means 会拟合出一个由 k 个簇中心点构成的模型，最优的簇中心点需要满足簇中的每个点到该中心的总距离最短。
其他重要的聚类算法还有高斯混合模型和谱聚类（详情请参考 Scikit-Learn 聚类文档， http://scikit-learn.org/stable/modules/clustering.html）。

4. 降维： 推断无标签数据的结构

降维其实就是在保证高维数据质量的条件下从中抽取出一个低维数据集。
通过Isomap 算法得到的可视化结果，颜色（表示算法提取到的一维潜在变量）沿着螺旋线呈现均匀变化，表明这个算法的确发现了肉眼所能观察到的结构。
一些重要的降维算法，包括主成分分析和各种流形学习算法，如 Isomap 算法、局部线性嵌入算法

5.2 Scikit-Learn简介

一、Scikit-Learn的数据表示

1. 数据表
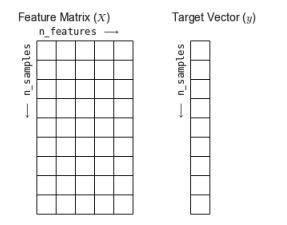
   基本的数据表就是二维网格数据，其中的每一行表示数据集中的每个样本，行数记为 n_samples；而列表示构成每个样本的相关特征，列数记为 n_features。
2. 特征矩阵X
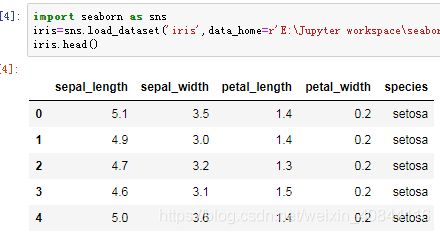
   表格布局通过二维数组或矩阵的形式将信息清晰地表达出来，所以我们通常把这类矩阵称为特征矩阵（features matrix） 。简记为变量 X。
   它是维度为 [n_samples, n_features]的二维矩阵，通常可以用 NumPy数组或Pandas的DataFrame来表示，不过Scikit-Learn也支持SciPy的稀疏矩阵。
   这里X=iris.drop(‘species’,axis=1)
3. 目标数组y
   除了特征矩阵 X 之外，我们还需要一个标签或目标数组，通常简记为 y。
   目标数组一般是一维数组，其长度就是样本总数 n_samples，通常都用一维的 NumPy 数组或 Pandas 的Series 表示。
   目标数组可以是连续的数值类型，也可以是离散的类型 / 标签。
   目标数组的特征通常是我们希望从数据中预测的量化结果；借用统计学的术语， y 就是因变量。
   这里y=iris[‘species’]

二、Scikit-Learn的评估器API

1. API基础知识

Scikit-Learn 评估器 API 的常用步骤如下：
(1) 通过从 Scikit-Learn 中导入适当的评估器类，选择模型类。
(2) 用合适的数值对模型类进行实例化，配置模型超参数（hyperparameter）。
(3) 整理数据，通过前面介绍的方法获取特征矩阵和目标数组。
(4) 调用模型实例的 fit() 方法对数据进行拟合。
(5) 对新数据应用模型：
• 在有监督学习模型中，通常使用 predict() 方法预测新数据的标签；
• 在无监督学习模型中，通常使用 transform() 或 predict() 方法转换或推断数据的性质。

2. 有监督学习示例： 简单线性回归

简单线性回归的建模步骤
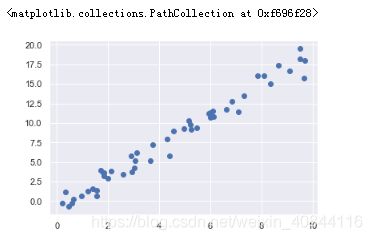
(1) 首先建立一个算点数据集

import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(42)
x = 10 * rng.rand(50)
y = 2 * x - 1 + rng.randn(50)
plt.scatter(x, y)

(2) 使用API
step1：选择模型类
每个模型类都是一个 Python 类，直接导入简单线性回归模型类

from sklearn.linear_model import LinearRegression

step2：实例化模型，选择模型超参数

model=LinearRegression(fit_intercept=True)
model
>>>LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

有一些重要的参数必须在选择模型类时确定好。这些参数通常被称为超参数
这一步是将模型类实例化了一个模型对象，并没有将模型应用到数据上。

step3：将数据整理成特征矩阵X和目标数组y
之前的x,y都是numpy数组，y不用处理，但是特征矩阵X是一个 [n_samples,n_features]形式二维数组或者矩阵，需要用dataframe或者numpy数组矩阵化。
数组或序列转成dataframe比较好操作，当n_features=1时，除了可以选择转成dataframe,还可以转成矩阵，参考：数组的变形

import pandas as pd
import numpy as np
#X=pd.DataFrame(x)
X=x[:,np.newaxis]
#X=x.reshape(y.shape[0],1)
#X

step4：训练模型，用模型拟合数据fit()

model.fit(X,y)
>>>LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

fit() 命令会在模型内部进行大量运算，运算结果将存储在模型属性中
可以理解成model在这一步进行了“成长”，拥有了“自己”的属性

model.coef_   #斜率
>>>array([1.9776566])
model.intercept_   #截距
>>>-0.9033107255311164

step5：预测新数据的标签 predict()
模型训练出来之后，有监督机器学习的主要任务就变成了对不属于训练集的新数据进行
预测。

#新数据,矩阵化
xfit = np.linspace(-1, 11)#num=50均匀分布数组
Xfit=xfit[:,np.newaxis]
#输入到模型中，输出拟合结果
yfit=model.predict(Xfit)
#可视化
plt.scatter(x,y)#y原数据
plt.plot(xfit,yfit)#拟合数据

3. 有监督学习示例： 鸢尾花数据分类

这里使用高斯朴素贝叶斯，这个方法假设每个特征中属于每一类的观测值都符合高斯分布。
因为高斯朴素贝叶斯方法速度很快，而且不需要选择超参数，所以通常很适合作为初步分类手段。

train_test_split()将数组或矩阵随机分割成训练集和测试集(详见5.3.1.2)

#准备数据
from sklearn.model_selection import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(X_iris,y_iris,random_state=1)

高斯朴素贝叶斯方法速度很快，而且不需要选择超参数#模型拟合数据

#使用模型预测标签
from sklearn.naive_bayes import  GaussianNB  #选择模型类
model=GaussianNB()                           #初始化模型
model.fit(Xtrain,ytrain)                     #模型拟合数据
y_model=model.predict(Xtest)                 #预测新数据

accuracy_score 工具:分类准确率分数

#验证模型结果的准确率
from sklearn.metrics import accuracy_score
accuracy_score(ytest,y_model)
>>>0.9736842105263158

4. 无监督学习示例： 鸢尾花数据降维

鸢尾花数据集由四个维度构成，即每个样本都有四个维度
降维的任务是要找到一个可以保留数据本质特征的低维矩阵来表示高维数据。
降维通常用于辅助数据可视化的工作

将使用主成分分析（principal component analysis， PCA）方法，这是一种快速线性降维技术。
我们将用模型返回两个主成分，也就是用二维数据表示鸢尾花的四维数据

from sklearn.decomposition import PCA   #选择模型类
model=PCA(n_components=2)				#初始化模型，选择超参数（主成分个数=2）
model.fit(X_iris)						#拟合数据，这里不用y变量
X_2D=model.transform(X_iris)			#降维（根据之前设定的主成分个数）

训练好的model通过transform()方法将数据降低纬度，降维后的矩阵就是按照设定后，只有两个特征

将降维好的数据分别添加带原表新列中，使用Seaborn 的 lmplot()方法画回归图

iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False)

如图所示，如果没有’species’列验证，就是图中没有颜色区分，该图形状上也能大致区分出三种类别的标签

5. 无监督学习示例： 鸢尾花数据聚类

聚类算法是要对没有任何标签的数据集进行分组,这里使用高斯混合模型Gaussian mixture model， GMM）。GMM 模型试图将数据构造成若干服从高斯分布的概率密度函数簇。

from sklearn.mixture import GaussianMixture#选择模型类
model=GaussianMixture(n_components=3,covariance_type='full')#设置超参数，初始化模型
model.fit(X_iris)#拟合数据，不需要y变量
y_gm=model.predict(X_iris)#确定簇标签

y_gm是一个数据类型是整形的数组，0,1,2开始，分别代表一个标签
将该标签添加到原表中便于画图

sns.lmplot("PCA1", "PCA2", data=iris, hue='species',col='cluster', fit_reg=False)

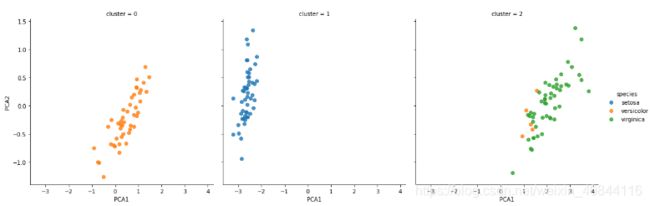
如图所示，模型已经将数据分成三类，在三个子图中，实际数据类别以’species’列用颜色区分，如图所示模型分类和实际分类已经大致重合

三、应用：手写数字探索

光学字符识别问题：手写数字识别。简单点说，这个问题包括图像中字符的定位和识别两部分。

1. 加载并可视化手写数字

step1:获取数据,来自sklearn自带数据集

from sklearn.datasets import load_digits
digits = load_digits()

---

---

延伸补充：
load_digits()数据集是手写数字数据集
digits的类型类似字典

type(digits)
>>>sklearn.utils.Bunch
digits.keys()
>>>dict_keys(['data', 'target', 'target_names', 'images', 'DESCR'])

每一个key对应不同维度的数组，每个key存储着不同的信息，digits.images存储着每张图像素信息

digits.images.shape
>>>(1797, 8, 8)

digits.images就是一个3维数组，有1797个8*8的矩阵（1797个8*8像素的图片）

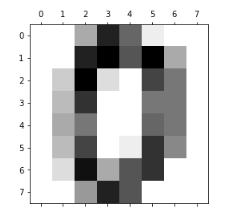
digits.images[0]

矩阵可视化工具matshow()画图，配色选择二进制（黑白），矩阵的数字大小就能表示颜色的深浅

plt.matshow(digits.images[0],cmap='binary')

这样就可以看出，图像是如何用数据表示的。

除了digits.images，digits其它key也存着相关的数据：
digits.target是一维数组，存储着每张图片对应的真实数字，这样它就是目标数组y；
digits.data是二维数组，可以看做将digits.images每张图的8*8二维矩阵降维成一维数组，这样digits.data就是一个二维特征矩阵X，两者关系可以这样表示：digits.images=digits.data.reshape(-1,8,8)

digits.data.shape
>>>(1797, 64)
digits.data[0]

---

---

step2：选取100张图，可视化绘制子图

import matplotlib.pyplot as plt
#设置画布和坐标
fig, axes = plt.subplots(10, 10, figsize=(8, 8),subplot_kw={
     'xticks':[], 'yticks':[]},gridspec_kw=dict(hspace=0.1, wspace=0.1))
#设置子图内容
for i, ax in enumerate(axes.flat):
    ax.imshow(digits.images[i], cmap='binary', interpolation='nearest')
    ax.text(0.05, 0.05, str(digits.target[i]),transform=ax.transAxes, color='green')

plt.subplots():

• subplot_kw-传入设置子图的关键字参数，这里是将刻度清空
• gridspec_kw-传入子图网格的关键字参数，这是是设置子图间横纵间隔为图的0.1

ax.imshow()

• cmap-图像的配色方案，这里是设置成二进制
• interpolation-插值，在图像上的反映就是边缘羽化程度

ax.text(）

• transform-坐标变换对象为子图坐标系
  

2. 无监督学习： 降维

[n_samples, n_features] 二维特征矩阵X和目标数组y已知如下

X = digits.data
X.shape
>>>(1797, 64)
y = digits.target
>>>(1797,)

有1797个样本和64个特征
对64为参数控件的样本进行可视化十分困难，因此需要借助无监督学习方法-降维-流形学习算法中的 Isomap对数据降成二维

from sklearn.manifold import Isomap#选择模型类
isomodel=Isomap(n_components=2)#设置超参数，初始化模型
isomodel.fit(X)#训练模型，拟合数据
data_projected_2D=isomodel.transform(X)#降低维度

data_projected_2D.shape
>>>(1797, 2)

这样数据就投影到二维，可视化这两个特征维度

plt.scatter(data_projected_2D[:, 0], data_projected_2D[:, 1], c=digits.target,edgecolor='none', alpha=0.5,cmap=plt.cm.get_cmap('Spectral', 10))
plt.colorbar(label='digit label', ticks=range(10))
plt.clim(-0.5, 9.5)#色阶范围

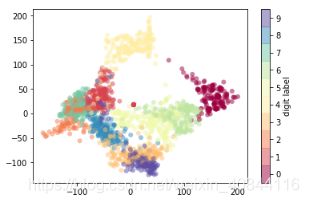
不同的颜色代表不同的数字，两种颜色的点团离得越远越不重合，说明他们特征越不相似

3. 数字分类

使用高斯朴素贝叶斯模型来分类
首先将数据分成训练集和测试集

from sklearn.model_selection import train_test_split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, random_state=0)

使用模型预测标签

from sklearn.naive_bayes import  GaussianNB  #选择模型类
model=GaussianNB()                           #初始化模型
model.fit(Xtrain,ytrain)                     #模型拟合数据
y_model=model.predict(Xtest)                 #预测新数据

验证模型结果的准确率

from sklearn.metrics import accuracy_score
accuracy_score(ytest,y_model)
>>>0.8333333333333334

这样的结果显示，使用高斯朴素贝叶斯模型，数字识别率就可以达到 80% 以上，但是无法知道该模型哪里做的不好，解决办法是用混淆矩阵(confusion matrix）

from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, y_model)#计算混淆矩阵

画出热图

import seaborn as sns
sns.heatmap(mat, square=True, annot=True, cbar=False,cmap='binary')#热图
plt.xlabel('predicted value')
plt.ylabel('true value')

如果是完美的识别，应该全部的predicted value=true value，图像上就应该是只有对角线的数据不等于0，识别有误差就会体现在非对角线格子里的非0数，例如true value=2，或被认作1或者8比较多

另一种显示模型特征的直观方式就是将样本画出来，左下角放预测值（之前放的是实际值），错误的值用红色字体标注

#设置画布和坐标
fig, axes = plt.subplots(10, 10, figsize=(8, 8),subplot_kw={
     'xticks':[], 'yticks':[]},gridspec_kw=dict(hspace=0.1, wspace=0.1))
#预测值的三维矩阵
test_images=Xtest.reshape(-1,8,8)#(升高一个维度(450, 64)-->(450, 8, 8))，-1是原矩阵的最外层维度
#画图
for i, ax in enumerate(axes.flat):
    ax.imshow(test_images[i], cmap='binary', interpolation='nearest')
    ax.text(0.05, 0.05, str(y_model[i]),transform=ax.transAxes,color='green' if (ytest[i] == y_model[i]) else 'red')

从测试集中仍旧取100个图片观察

如果需要替身专区额率，需要更加复杂色算法，例如支持向量机、随机森林等其他算法

5.3 超参数与模型验证

在有监督机器学习模型基本步骤中，前两步“模型选择和超参数选择”可能是有效使用各种机器学习工具和技术最重要的阶段。我们需要胰脏能方式来验证选中的模型和超参数是否可以很好地拟合数据。

一、 什么是模型验证

模型验证就是在选择模型和超参数之后，通过对训练数据进行学习，对比模型对已知数据的预测值与实际值的差异。

1.错误的模型验证方法

从sklearn自带数据集中加载数据

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target

k 近邻分类器，超参数为 n_neighbors=1（k=1），新数据的标签与其最接近的训练数据的标签相同

from sklearn.neighbors import KNeighborsClassifier
model=KNeighborsClassifier(n_neighbors=1)
model.fit(X,y)
y_model=model.predict(X)

预测数据

from sklearn.metrics import accuracy_score
accuracy_score(y,y_model)
>>>1.0

准确率是100%，因为训练模型用的是X，预测数据也是X。。
最近邻模型是一种与距离相关的评估器，只会简单地存储训练数据，然后把新数据与存储的已知数据进行对比来预测标签。
相当于训练的时候，告诉模型张三是A类，预测的时候有一个一模一样的张三跑进来，模型看了看离他最近或者说重叠的那个原张三（k=1只看一个人），自然100%判断他是A类。

2.模型验证正确方法： 留出集train_test_split()

先从训练模型的数据中留出一部分，然后用这部分留出来的数据来检验模型性能。

from sklearn.model_selection import train_test_split
X_train, X_predict, y_train, y_predict = train_test_split(X, y, random_state=0,train_size=0.5)

注意：

• 新的模块sklearn.model_selection，将以前的sklearn.cross_validation, sklearn.grid_search 和 sklearn.learning_curve模块组合到一起
• train_test_split()方法可以设置test_size和train_size,当两者都未指定时，test_size默认样本比例是0.25,当其中一个指定时，另一个就是其补集

model.fit(X_train,y_train)
>>>KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')

y2_model=model.predict(X_predict)
accuracy_score(y_predict,y2_model)
>>>0.9066666666666666

这里的训练集和测试集是完全无接触的

3.交叉检验

留出集进行模型验证有一个缺点，就使模型失去了一部分训练机会。
交叉检验就是做一组拟合，让数据的每个子集既是训练集，又是验证集。
1）两个子集轮流

from sklearn.model_selection import train_test_split
X_train, X_predict, y_train, y_predict = train_test_split(X, y, random_state=0,train_size=0.5)

from sklearn.neighbors import KNeighborsClassifier
model=KNeighborsClassifier(n_neighbors=1)

y_model_tp=model.fit(X_train,y_train).predict(X_predict)
y_model_pt=model.fit(X_predict,y_predict).predict(X_train)

from sklearn.metrics import accuracy_score
accuracy_score(y_predict,y_model_tp),accuracy_score(y_train,y_model_pt)
>>>(0.9066666666666666, 0.96)

3）多个子集轮流
cross_val_score简单实现

from sklearn.cross_validation import cross_val_score
cross_val_score(model,X,y,cv=5)
>>>array([0.96666667, 0.96666667, 0.93333333, 0.93333333, 1.        ])

3）LOO（leave-one-out，只留一个）交叉检验
我们每次只剩一个样本做测试，其他样本全用于训练

from sklearn.cross_validation import cross_val_score
from sklearn.cross_validation import LeaveOneOut
scores = cross_val_score(model, X, y, cv=LeaveOneOut(len(X)))
scores
>>>
>array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 0., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

一共len(X)轮，每轮只需要验证那个省下来的样本，要么是100%,要么是0
计算该结果的平均值

scores.mean()
>>>0.96

二.选择最优模型

1.偏差与方差的均衡

“最优模型”的问题基本可以看成是找出偏差与方差平衡点的问题。
高偏差-欠拟合-模型没有足够的灵活性来适应数据的所有特征-模型在验证集的训练集表现类似
高方差-过拟合-模型过于灵活，在适应数据所有特征的同时，也适应了随机误差-模型在验证机的表现远远不如在训练集的表现
得分：R²判定系数，1表示模型与数据完全吻合，0表示模型不必简单取均值好，为负表示模型性能很差。
验证曲线：如果可以调整模型的复杂度，训练得分和验证得分的变化趋势
不同模型复杂度的调整方法大不相同。

2.Scikit-Learn验证曲线

多项式回归模型
多项式，例如y = ax³+ bx² + cx + d

• 创建数据

import numpy as np
def make_data(N, err=1.0, rseed=1):
    # 随机轴样数据
    rng = np.random.RandomState(rseed)
    X = rng.rand(N, 1) ** 2
    y = 10 - 1. / (X.ravel() + 0.1)
    if err > 0:
        y += err * rng.randn(N)
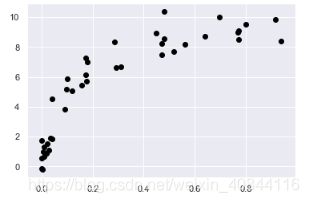
    return X, y
X, y = make_data(40)

---

np.raval()：将多维数组降为一维

X.shape
>>>(40, 1)
X.ravel().shape
>>>(40,)

[:None]：将增加一个维度，维度长度是1

X_test.shape
>>>(500,)
X_test[:,None].shape
>>>(500, 1)

---

• 绘图查看

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set() # 设置图形样式
plt.scatter(X.ravel(), y, color='black')

• 多项式回归模型

from sklearn.preprocessing import PolynomialFeatures#多项式特征
from sklearn.linear_model import LinearRegression#线型回归模型
from sklearn.pipeline import make_pipeline#管道命令

def PolynomialRegression(degree=2,**kwargs):#自定义的多项式回归模型
    return make_pipeline(PolynomialFeatures(degree),LinearRegression(**kwargs))

• 拟合数据

#均匀分割的二维单列数组
X_test=np.linspace(-0.1,1.1,500)[:,None]

#3个不同等级下的y_test
for degree in [1, 3, 5]:
	#4步：选择模型-设置超参数-拟合数据训练模型-预测数据
    y_test = PolynomialRegression(degree).fit(X, y).predict(X_test)
    #绘图
    plt.plot(X_test.ravel(), y_test, label='degree={0}'.format(degree))

#之前创造的数据
plt.scatter(X.ravel(), y, color='black')

plt.xlim(-0.1, 1.0)#x周刻度范围
plt.ylim(-2, 12)#y轴刻度范围
plt.legend(loc='best')#以'best'位置展示图例

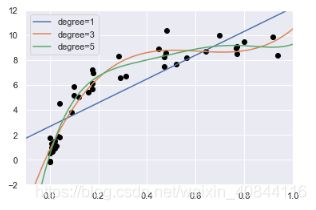从改图可以看到，不同的degree的拟合程度不一样，但是具体哪个更好不能直观感受，需要用得分（训练得分和验证得分）量化

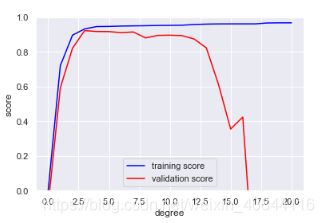
• 绘制验证曲线

from sklearn.learning_curve import validation_curve
degree=np.arange(0,21)
train_score, val_score = validation_curve(PolynomialRegression(), X, y,'polynomialfeatures__degree',degree, cv=7)#cv交叉验证

21个degree，每个degree下每次交叉验证7次
取每次验证的中位数作为每个degree的得分

#取中位数
train_score_m=np.median(train_score,1)
train_score_m=np.median(val_score,1)

#绘图
plt.plot(degree, train_score_m, color='blue', label='training score')
plt.plot(degree, val_score_m, color='red', label='validation score')

plt.legend(loc='best')#设置图例
plt.ylim(0,1)#y坐标刻度
plt.xlabel('degree')
plt.ylabel('score')

如图所示，degree=3时偏差和方差均衡性最好

三、学习曲线

1.训练集大小和模型效果

上一节用多项式模型系数来控制模型复杂度以改变模型效果，另一个重要因数是训练集的数据量

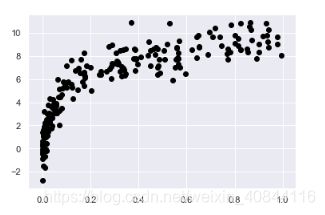
• 使用更多的训练数据

X2,y2=make_data(200)
plt.scatter(X2.ravel(), y2, color='black')

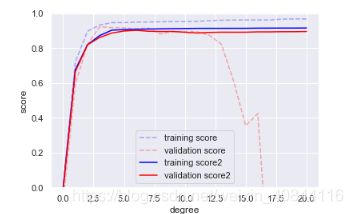
• 绘制新的验证曲线

train_score, val_score = validation_curve(PolynomialRegression(), X, y,'polynomialfeatures__degree',degree, cv=7)#cv交叉验证
train_score2, val_score2 = validation_curve(PolynomialRegression(), X2, y2,'polynomialfeatures__degree',degree, cv=7)#cv交叉验证

plt.plot(degree, np.median(train_score, 1), color='blue', label='training score',alpha=0.3,linestyle='dashed')
plt.plot(degree, np.median(val_score, 1), color='red', label='validation score',alpha=0.3,linestyle='dashed')

plt.plot(degree, np.median(train_score2, 1), color='blue', label='training score2')
plt.plot(degree, np.median(val_score2, 1), color='red', label='validation score2')


plt.legend(loc='lower center')
plt.ylim(0, 1)
plt.xlabel('degree')
plt.ylabel('score')

如图所示，之前的小训练集，degree取到3就比较合适了，后来的大数据训练集体取更大的degree都支持，验证分和训练分都比较接近。
两个影响模型效果的因素：模型复杂度和训练数据集的规模。
学习曲线：反映训练集规模的训练得分 / 验证得分曲线
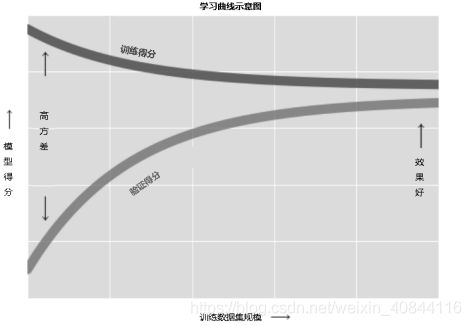学习曲线最重要的特征是，随着训练样本数量的增加，分数会收敛到定值。因此，一旦你的数据多到使模型得分已经收敛， 那么增加更多的训练样本也无济于事！ 改善模型性能的唯一方法就是换模型（通常也是换成更复杂的模型）

2.Scikit-Learn学习曲线

learning_curve函数

from sklearn.model_selection import learning_curve
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

#次数为2和次数为9 的多项式
for i, degree in enumerate([2, 9]):
    N, train_lc, val_lc = learning_curve(PolynomialRegression(degree),X, y, cv=7,train_sizes=np.linspace(0.3, 1, 25))#4步骤
    ax[i].plot(N, np.mean(train_lc, 1), color='blue', label='training score')#训练集的学习曲线
    ax[i].plot(N, np.mean(val_lc, 1), color='red', label='validation score')#验证集的学习曲线
    ax[i].hlines(np.mean([train_lc[-1], val_lc[-1]]), N[0], N[-1], color='gray',linestyle='dashed')#水平分割线
    
    ax[i].set_ylim(0, 1)#y轴刻度
    ax[i].set_xlim(N[0], N[-1])#轴刻度
    ax[i].set_xlabel('training size')
    ax[i].set_ylabel('score')
    ax[i].set_title('degree = {0}'.format(degree), size=14)
    ax[i].legend(loc='best')

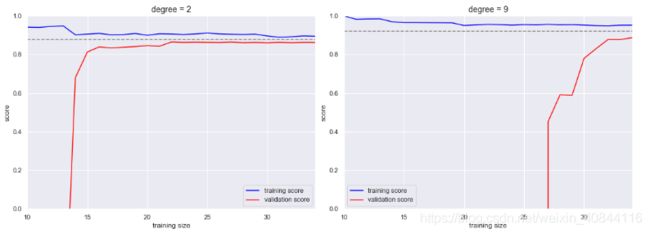
如左图所示：随着training size的增大，训练得分和验证得分都趋于接近，但是较简单的二次多项式模型在training size位于15的时候两者收敛到已经接近重合，再怎么增大training size也不能显著改善拟合效果。
如右图所示：采用复杂度更高的模型之后，虽然学习曲线的收敛得分提高了（对比虚线所在位置），但是模型的方差也变大了（对比训练得分与验证得分的差异即可看出）。如果我们为复杂度更高的模型继续增加训练数据，那么学习曲线最终也会收敛。

四、验证实践： 网格搜索

有了偏差与方差的均衡直观的认识，它们与模型的复杂度（验证曲线）和训练集的大小（学习曲线）有关。在实际工作中，模型通常会有多个得分转折点，因此验证曲线和学习曲线的图形会从二维曲线变成多维曲面。
这种高维可视化很难展现，因此从图中找出验证得分的最大值也不是一件简单的事。Scikit-Learn 在model_selection （grid_search）提供了一个自动化工具解决这个问题–GridSearchCV 元评估器

from sklearn.model_selection import GridSearchCV

#多项式次数搜索范围，是否拟合截距，是否需要标准化处理
param_grid = {
      'polynomialfeatures__degree': np.arange(21),
               'linearregression__fit_intercept': [True, False],
               'linearregression__normalize': [True, False]}

#初始化评估器
grid = GridSearchCV(PolynomialRegression(), param_grid, cv=7)

#拟合数据，训练评估器
grid.fit(X, y)

#查看评估器属性-最优参数
grid.best_params_

>>>
{
     'linearregression__fit_intercept': False,
 'linearregression__normalize': True,
 'polynomialfeatures__degree': 4}

这样评估器就给出一个答案：该多项式回归模型最优解是需要拟合截距，不需要标准化数据，最优的次数是4

使用这个评估器给我的模型，去拟合验证数据，并画图

X_test = np.linspace(-0.1, 1.1, 500)[:, None]#验证集

model = grid.best_estimator_#评估器的模型
y_test = model.fit(X, y).predict(X_test)#预测验证集

plt.scatter(X.ravel(), y)
lim = plt.axis()
plt.plot(X_test.ravel(), y_test);
plt.axis(lim)

5.4 特征工程sklearn.feature_extraction

之前的示例都假设已经拥有一个干净的[n_samples,n_features]特征矩阵，但现实工作中，数据很少会这么干净。因此本节介绍及其学习实践中更重要的步骤之一特征工程：找到与问题有关的任何信息，把他们转换成特征矩阵的数值。
本节将介绍特征工程的一些常见示例：表示分类数据的特征、表示文本的特征和表示图像的特征。另外，还会介绍提高模型复杂度的衍生特征和处理缺失数据的填充方法。这个过程通常被称为向量化，因为它把任意格式的数据转换成具有良好特性的向量形式。

一、分类特征

一种常见的非数值数据类型是分类数据，可以有两种编码

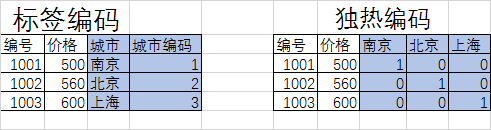
但是，Scikit-Learn 这个程序包的所有模块都有一个基本假设，那就是数值特征可以反映代数量（123具有代数意义），所以常用的解决方式就是独热编码：它可以有效增加额外的列，让 0 和 1 出现在对应的列分别表示每个分类值有或无。

data = [
{
     'price': 850000, 'rooms': 4, 'neighborhood': 'Queen Anne'},
{
     'price': 700000, 'rooms': 3, 'neighborhood': 'Fremont'},
{
     'price': 650000, 'rooms': 3, 'neighborhood': 'Wallingford'},
{
     'price': 600000, 'rooms': 2, 'neighborhood': 'Fremont'}
]

数据是字典列表时，ScikitLearn 的 DictVectorizer 类

from sklearn.feature_extraction import DictVectorizer
vec=DictVectorizer(sparse=False,dtype=int)#初始化
vec.fit_transform(data)#转换
>>>array([[     0,      1,      0, 850000,      4],
       [     1,      0,      0, 700000,      3],
       [     0,      0,      1, 650000,      3],
       [     1,      0,      0, 600000,      2]], dtype=int32)

查看特征名

vec.get_feature_names()#获取特征名
>>>['neighborhood=Fremont',
 'neighborhood=Queen Anne',
 'neighborhood=Wallingford',
 'price',
 'rooms']

注意：pandas中类似功能分类工具get_dummies()

二、文本特征

将文本转换成一组数值

sample = ['problem of evil',
          'evil queen',
          'horizon problem']

使用工具CountVectorizer

from sklearn.feature_extraction.text import CountVectorizer
vec=CountVectorizer()#初始化
X=vec.fit_transform(sample)#转换
X
>>>
<3x5 sparse matrix of type 'numpy.int64'>'
	with 7 stored elements in Compressed Sparse Row format>

得到一个系数矩阵，转换成dataframe

import pandas as pd
pd.DataFrame(X.toarray(),columns=vec.get_feature_names())

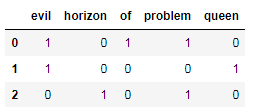
原始的单词统计会让一些常用词聚集太高的权重，在分
类算法中这样并不合理。解决这个问题的方法就是通过 TF–IDF,通过单词在文档中出现的频率来衡量其权重.

 from sklearn.feature_extraction.text import TfidfVectorizer
vec = TfidfVectorizer()
X = vec.fit_transform(sample)
pd.DataFrame(X.toarray(), columns=vec.get_feature_names())

三、图像特征

http://scikit-image.org

四、衍生特征

还有一种有用的特征是输入特征经过数学变换衍生出来的新特征。
例如将一个线性回归转换成多项式回归时，并不是通过改变模型来实现，而是通过改变输入数据。这种处理方式有时被称为基函数回归
定义数据

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1, 2, 3, 4, 5])
y = np.array([4, 2, 1, 3, 7])

使用简单线性回归，模拟效果很差

from sklearn.linear_model import LinearRegression
X = x[:, np.newaxis]
model = LinearRegression().fit(X, y)
yfit = model.predict(X)
plt.scatter(x, y)
plt.plot(x, yfit)

原始的数据拟合效果不好，那就需要更复杂的模型，将原数据多增加几个特征项来提升模型复杂度，衍生特征矩阵如下
第 1 列表示 x，第 2 列表示 x²，第 3 列表示 x³。

#多项式特征
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3, include_bias=False)#指定次数为3
X2 = poly.fit_transform(X)#转化成一个二维矩阵，新增维度的长度为3
print(X2)

这样获得了拟合效果更好的模型

 model = LinearRegression().fit(X2, y)
yfit = model.predict(X2)
plt.scatter(x, y)
plt.plot(x, yfit)

这种不通过改变模型，而是通过变换输入来改善模型效果的理念，正是许多更强大的机器学习方法的基础。

五、缺失值填充Imputer

from numpy import nan
X = np.array([[ nan, 0, 3 ],
              [ 3, 7, 9 ],
              [ 3, 5, 2 ],
              [ 4, nan, 6 ],
              [ 8, 8, 1 ]])

使用Imputer快速填充空值

from sklearn.preprocessing import Imputer
imp=Imputer(strategy='mean')
X2=imp.fit_transform(X)
X2
>>>
array([[4.5, 0. , 3. ],
     [3. , 7. , 9. ],
     [3. , 5. , 2. ],
     [4. , 5. , 6. ],
     [8. , 8. , 1. ]])

六、管道特征

管道特征可以将多个操作串起来

from sklearn.pipeline import make_pipeline
model = make_pipeline(Imputer(strategy='mean'),
					  PolynomialFeatures(degree=2),
					  LinearRegression())

这里包含3个步骤：
(1) 用均值填充缺失值。
(2) 将衍生特征转换为二次方。
(3) 拟合线性回归模型。
组合起来的管道就如同一个标准的 Scikit-Learn 对象，可以对任何输入数据进行所有步骤的处理