Market Risk Modeling

Market Risk Modeling

Market Risk

• interest-rate risks
• equity risks
• exchange rate risks
• commodity risks

Traditional risk mesurement tools

1. Gap analysis

   Ideas of interest-rate risk exposure

   $$\Delta NII=(GAP)\Delta r$$

   $\Delta NII$ 为净利率收入变化，$\Delta r$ 为利率变化

   对时间线的选择比较敏感

2. Duration analysis

   久期分析，测量利率风险

   麦考利久期 $D={\sum }_{i=1}^n[i\times PVC{F}_i]/{\sum }_{i=1}^{n}PVC{F}_i$ ，$PVC{F}_i$ 是第 $i$ 期的折现现金流。久期给出了债卷价格相对其收益变化的敏感度的近似指标:

   %Change in bond price = $-D\times \Delta y/(1+y)$

   久期越大，收益变化对债卷价格影响越大。久期比较容易计算，相对于Gap Analysis，它审视了整个资产或负债的变化，而不是只关心净收入。但是久期也只针对于利率风险。

3. Scenario Approach

   ​ 场景分析方法主要是构造不同的场景，并分析在这些场景下的所得和所失。场景的影响因素就包括诸如股票价格、利率和汇率等，同时研究资产和负债的现金流和折现值，从而得到风险敞口。

   场景方法并不容易实施，构造一个正确的场景也非常困难，我们需要覆盖最可能的情况且考虑变量之间的相关性。

4. 投资组合理论

   ​ 投资组合理论认为投资者在配资投资组合时会基于资产的期望收益和收益标准差，组合收益的标准差就是风险的度量。显然，投资者会在同等风险上追求更高的收益，且权衡风险和收益。

   ​ 在这种理论框架下，在投资组合中的某个资产的风险不仅仅和其本身有关，还和整个组合的相关性有关；或者说一个资产对整个组合的风险贡献度依赖于资产与组合协方差除以组合收益的方差(或称为贝塔)。

   ​ 投资组合理论提供了一个可以处理多风险和风险之间的交互作用，它被基金经理，投资管理者广泛使用。但事实上，其参数诸如协方差，期望收益等并不容易估算，它需要大量数据。

5. 衍生品风险度量(Derivatives Risk Measures)

   ​ 我们可以通过以下参数来估算衍生品头寸风险:

   • $\Delta$ ：代表底层资产价格的小变化导致的衍生品价格变化

   • $\gamma$ ：底层资产价格的小变化导致的 $\Delta$ 的变化 (二阶导数)

   • $\rho$ ：利率变化导致的衍生品价格变化

   • Vega : $\partial V/\partial \sigma$ , 波动率的变化导致的衍生品价格变化

   • $\theta$ ： 时间的推移导致衍生品价格的变化

     使用这些度量指标，我们必须知道它们必须服从动态对冲策略，只针对于风险因子的小变化，需要经常检查。当市场有大的变化是，这些指标往往不能再说明问题。

VaR （Value at Risk)

• 在险价值(VaR)的出处

  ​ VaR来自于JP Morgan的RiskMetrics系统，设计为可以度量风险跨越不同的交易头寸，跨越整个机构，而且可把多个风险聚集为一个单一的风险度量。该系统采用了VaR，即在下一个交易日的最大可能损失。VaR是基于标准的投资组合理论的，会估算不同交易工具的标准差和相关系数，虽然看上去比较直接，但是实际上使其称为系统化方法还是有大量的工作要做的，例如测度惯例选择、构造数据集、统计假设、估算波动率和相关性的步骤等。

  ​ 随后，很多机构都开始开发各自的VaR系统，有通过收益和损失直方图来估算的，也有采用蒙特卡洛模拟的；后来VaR被扩展到信用风险、流动性风险和现金流风险。

• VaR的优点

  • 提供通用的、跨越不同头寸和风险因子的风险度量工具
  • 考虑了风险因子之间的相关性

• 关于VaR的指责

  • 可验证性及其统计假设

    对于社会体系中的智能体而言，他们会学习如何对所处的环境做出反应，致使市场中的很多过程是非平稳且具备动态依赖关系。这会使VaR在有些情况下呈现错误的结果。一个例子是长期资本管理公司(Long Term Capital Management)发现在1998年的秋季和夏季，损失是正常收益损失的14个标准差。

  • 估算方法不明确

    经验告诉我们多种多样的VaR的估算方法给出了不同的结果，这说明VaR带来了实现方法风险。

  • VaR会带来向下偏差

  • VaR会带来高度下行相关性

  • VaR并不是最佳的尾部风险度量

    VaR不具备一致性属性，因此ETL(Expected Tail Loss)进入了这个舞台。

• What is VaR

  

  给定一个期间，在95%的置信水平下，亏损不会超过1.645.

  

  给定一个期间，在99%的置信水平下，亏损不会超过2.326

VaR与置信水平.

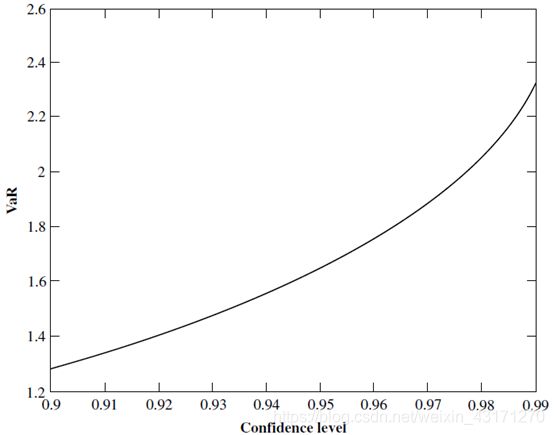
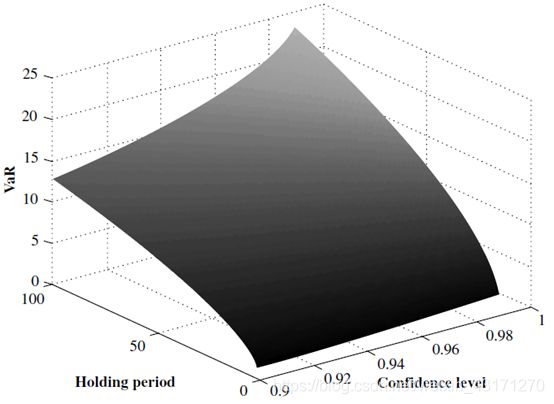
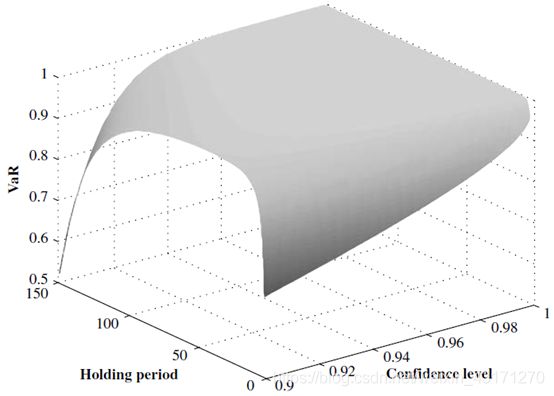
VaR与持有期间

VaR平面

• VaR参数
  • Holding Period
  • Confidence Interval

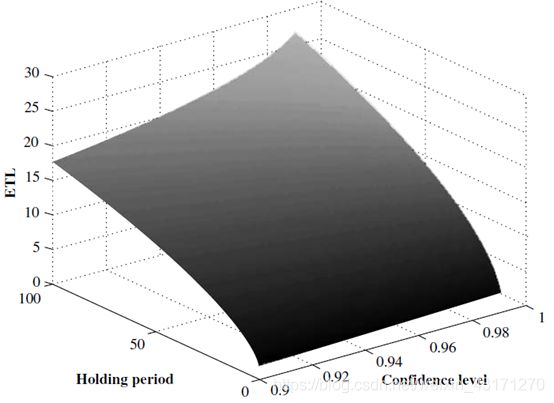
Expected Tail Loss (ETL)

• Coherent Risk Measures

  如果 $X$ , $Y$ 是两个风险头寸的价值，$\rho$ 代表风险度量，

  $$\rho (X)+\rho (Y)\le \rho (X+Y)$$ , sub-additivity

  $$\rho (tX)=t\rho (X)$$ , homogeneity

  $$\rho (X)\ge \rho (Y),ifX\le Y$$ , monotonicity

  $$\rho (X+n)=\rho (X)-n$$ , risk-free condition

  满足这四个条件的风险度量称为连贯风险度量。前三个条件保证 $\rho$ 为凸函数，最后一个条件说明当某头寸加上一个确定的无风险资产会减少其风险。

• What is ETL

  ETL还有其他名字，例如Expected Shortfall, Conditional VaR(CVaR)等。

  $$ETL=E[L|L>VaR]$$

  L 代表损失，ETL就是如果损失大于 VaR 的时候，损失的期望价值。

  

  
  

  Basic Issues in Measureing Market Risk

• 数据问题

  • Profit/Loss Data

    $$P/L_t=P_t+D_t-P_{t-1}$$, $D_t$ 为期间支付

    Present Value $(P/L_t)=(P_t+D_t)/(1+d)-P_{t-1}$

    Forward Value$P/L_t)=P_t+D_t-(1+d)P_{t-1}$

    其中， $d$ 为折现率。

  • Loss/Profit Data

    $$L/P_t=-P/L_t$$

  • Arithmetric Returns Data

    $$r_t=(P_t+D_t-P_{t-1})/P_{t-1}$$

  • Geometric Returns Data

    $$R_t=log[(P_t+D_t)/P_{t-1}]=log(1+r_t)$$

• 如何估算VaR

  • Historical Simulation

    Ordered L/P observations

  

  • Parametric VaR

    明确定义观测值的统计分布

    1. 正态分布：

    $$VaR=-{\alpha }_{cl}{\sigma }_{P/L}-{\mu }_{P/L}$$

    2. Normally Distributed Arithmetic Returns

    $$VaR=-({\mu }_r+{\alpha }_{cl}{\sigma }_r)P_{t-1}$$

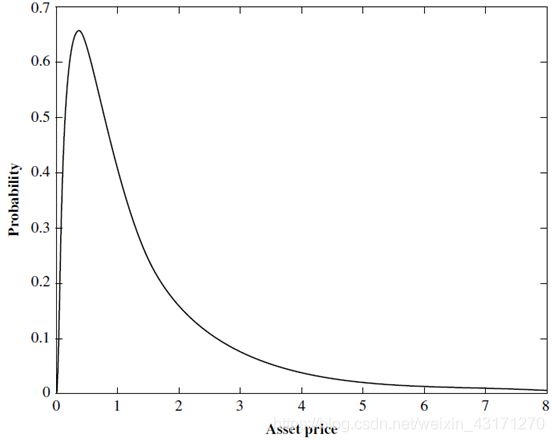
    3. Lognormal VaR

    $$VaR=P_{t-1}-exp[{\mu }_R+{\alpha }_{cl}{\sigma }_R+log{P}_{t-1}]$$

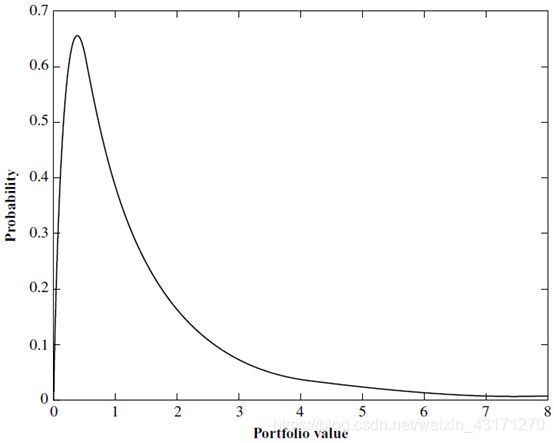
    log normal asset price

  

  Lognormal VaR

  

• 如何估算ETL

  ETL实际上是概率权重尾部损失的平均值，或者超过VaR的损失。

  正常的VaR和ETL

  

  非参数估算方法(VaR,ETL)

  ​ 事实上，非参数法在估算VaR和ETL上更为普遍。这种方法并不对收益分布进行任何统计假设，它们主要依靠数据说话，但是它们共同依赖的假设是历史数据能近似表示未来。

  • 历史模拟(Historical Simulation)

  • 估算VaR/ETL曲线和曲面

  • 估算置信区间

    标准错误 $se(x)=\sqrt{p(1-p)/(n{f}^2)}$, $f$ 为概率密度函数值；$p$ 为累积密度函数值

    1）Order Statistic Approach

    2）Bootstrap Approach

  • 加权历史模拟(Weighted Historical Simulation)

    • Age-Weighted
    • Volatility-Weighted

  • Filtered Historical Simulation (FHS)

    传统的方法并不能适应条件变化波动率，而这些波动率比较自然的模型是GARCH，但是GARCH模型需要我们定义收益过程(return process)，这一点并不适合于无参模型。FHS方法结合HS的优势和GARCH对条件波动率建模的灵活能力。

    假如我们想用FHS来估算一个单资产的投资组合在一天的VaR:

    1）第一步，用一个GARCH模型拟合观测数据，我们选择AGARCH(Asymmetric GARCH):

    $$r_t=\mu +{ϵ}_t$$

    $${\sigma }_t^2=\omega +\alpha ({ϵ}_{t-1+\gamma })+\beta {\sigma }_{t-1}^2$$

    2）第二步，使用这个模型在采样期间中预测每一天的波动率，而这些波动率可以被分成实现的收益产生一个标准化的成iid(independent identically distribution)的收益集合.

    3）第三步，对这个集合进行bootstrapping采样

    4）最后，用这个新得到的收益集合来估算VaR。

    这种方法通过采用多变量GARCH模型可以适用于多资产的组合，也可以用来估算ETL。

  PCA to estimate VaR and ETL

  ​ 主成分分析法提供了一种对数据中存在的风险因子的简单表示，PCA应用于VaR和ETL的典型应用是针对于固收类投资组合。固收类产品在跨越利率期限结构时会有波动，在这种情况下，会呈现许多高度相关的风险因子，高维和共线性会使协方差矩阵难以估算，经验表明前三个主成分一般会覆盖95%的波动性。

  ​ 因子分析(Factor Analysis)着重于解释相关性，它在解释很多变量的相关性时非常有用。

  ​ 这些方法配合顺序统计量(Order Statistics)和bootstrap方法可以帮助我们估算VaR和ETL的置信区间。

  Parametric VaR and ETL

  • Normal

  • The Student t-distribution

    $$VaR(hp,cl)=-{\alpha }_{cl,v}\sqrt{hp}\sqrt{(v-2)/v}{\sigma }_{P/L}-hp{\mu }_{P/L}$$ , $hp$ 为holding period，$v$ 为自由度

  • Lognormal Distribution

    

  
  $$VaR=P_{t-1}-exp[hp{\mu }_R+{\alpha }_{cl}\sqrt{hp}{\sigma }_R+log{P}_{t-1}]$$

  • Extreme Value Distribution

    ​ Fisher–Tippett theorem 告诉我们如果 $X$ 有合适的’well-behaved’的分布函数 $F(X)$ ，那么 $X$ 的极值的分布函数会渐渐收敛于广义极值分布函数(GEV, Generalized Extreme Value):

    ​ If $\xi \ne 0$, $H_{\xi ,a,b}=exp[-(1+\xi (x-a)/b{)}^{-1/\xi }]$

    ​ else, $H_{\xi ,a,b}=exp[-exp(-(x-a)/b)]$

    $$\xi >0$$ 时，为Gumbel分布，$VaR=a-(b/\xi )[1-(-log(cl{)}^{-\xi }]$

    $$\xi =0$$ 时，为Frechet分布，$VaR=a-blog(log(1/cl))$

    

    ​ Grumbel VaR Surface

    ​ 我们可以应用EVT到超过阈值的超额损失的分布，称为广义帕累托分布(Generalized Pareto Distribution):

    ​ 如果 $X$ 的分布函数为 $F(X)$ , $u$ 时 $X$ 的阈值，定义 $X$ 超过 $u$ 的分布为

    $$F_u(X)=Pr\{X-u\le y|X>u\}$$ ,

    此分布函数收敛于广义帕累托分布：

    If $\xi \ne 0$ , $G_{\xi ,\beta }(x)=1-(1+x\xi /\beta {)}^{-1/\xi }$

    else , $G_{\xi ,\beta }(x)=1-exp(-x/\beta )$

    这里，$\beta >0$ 为尺度参数，$\xi$ 为形状参数，我们比较感兴趣的是 $\xi >0$ 的情况，意味着收入分布具备厚尾，

    $$VaR=u+(\beta /\xi )\{[(n/N_u)(1-cl){]}^{-\xi }-1\}$$

    $$ETL=[VaR+(\beta -\xi u)]/(1-\xi )$$

    其中，$\xi <1$, $n$ 为样本数量，$N_u$ 为超额值的数量。

  • Multivariate Normal Variance-Covariance

    前面所讨论的都是关于单一资产，多个资产的投资组合常用多元正态分布来建模，

    $$VaR(hp,cl)=-[{\alpha }_{cl}\sqrt{hp}\sqrt{w\Sigma w^T}+hpw\mu ]P$$

    $$ETL(hp,cl)=[\sqrt{hp}\sqrt{w\Sigma w^T}\varphi (-{\alpha }_{cl})/F({\alpha }_{cl})-hpw\mu ]P$$

  基于模拟技术的VaR/ETL估算

  ​ 首先需要强调，一般只在直接的估算方法不可用的情况下，才会使用模拟技术来估算VaR/ETL，例如组合包含多种期权。最自然的模拟方法是模拟中的模拟，我们模拟期权的底层资产的各种情况，模拟所有这些情况下的离散点的期权价值，也可以模拟底层变量，但是计算复杂度非常高。因此，我们需要在精确率和速度上做权衡。

  ​

  • 期权VaR和ETL

    举例来说，假如我们想要估算一个美式put option的VaR和ETL，运用模拟技术需要嵌入一个期权定价模型伴随股票价格的模拟路径。最简单的模型是二叉树模型，采用的参数如下：

    $$S(0)=X=1$$ ，$r=\mu =0$ ，$\sigma =0.25$ ，maturity = 1 year ，$cl=0.95$ ，hp = 1 day

    $$N=20$$ 步，$M=1000$ trials

    得到 $VaR=0.021$ ，置信区间为$[0.019,0.022]$

    $$ETL=0.026$$ ，置信区间为$[0.025,0.026]$

    我们可以通过优化来缩减计算时间：

    • 控制变化
    • 重要性采样
    • 分层采样
    • 动量匹配

  • 模拟主成分

    ​ 对一个固收类投资组合，我们首先选择一系列主要的零息利率 $[r_1,r_2,\cdots ,r_n]$ ，每一个都有不同的到期时间。对每一个利率用几何布朗运动建模，$d{r}_i/r_i={\mu }_i(t)dt+{\sigma }_{i}d{z}_i(t)$ ，$z_i(t)\sim N(0,\sqrt{t})$ ，$z_i(t)$ 会呈现非常高的相关性。我们通常会发现即期利率曲线的前三个主成分可以解释95%以上的波动。第一个主成分可以解释为平移因子(shift factor)；第二个主成分可以解释为坡度因子(slope factor)；第三个主成分为曲率因子。

    ​ 我们让 $C=[{\rho }_{i.j}]$ 为其相关矩阵，第 $j$ 个特征向量为 ${\beta }_j=[{\beta }_{1,j},{\beta }_{2,j},\cdots ,{\beta }_{n,j}]$ ，通过特征向量定义，我们有

    $$C{\beta }_j={\lambda }_j{\beta }_j$$ , $j=1,2,\cdots ,n$ ，${\lambda }_j$ 为第 $j$ 个特征值。

    规范化 $\beta$ 使得 $|{\beta }_j{|}^2={\sum }_{i=1}^n{\beta }_{i,j}^2={\lambda }_j$ , 并且使得 ${\lambda }_j$ 从大到小排序，可以把 $d{z}_i$ 写成

    $$d{z}_i=\sum _{j=1}^n{\beta }_{i,j}d{w}_j\approx {\beta }_{i,1}d{w}_1+{\beta }_{i,2}d{w}_2+{\beta }_{i,3}d{w}_3$$ ，$i=1,2,\cdots ,n$

    对于 $k\ne j$ ，$E[w_k\cdot w_j]=0$ ；$d{w}_j=\sqrt{dt}$ ,

    可以得到 $d{r}_i/r\approx {\mu }_i(t)dt+{\sigma }_i{\beta }_{i,1}d{w}_1+{\sigma }_i{\beta }_{i,2}d{w}_2+{\sigma }_i{\beta }_{i,3}d{w}_3$

  • 场景模拟

    我们可以通过场景模拟方法在PCA的基础上进一步缩减计算量。三个主成分 $d{w}_1,d{w}_2,d{w}_3$ 中的每一个都可以允许有限状态中的一个状态，我们可以从多项式分布中抽取其状态。一个主成分如果可以取 $m+1$ 个状态，那么状态 $i$ 的概率为：

    $$P(i)=2^{-m}\frac{m!}{i!(m-i)!}$$ ，$i=0,1,\cdots ,m$

    假如共有5个状态，概率分别为

    $$\frac{1}{16},\frac{1}{4},\frac{3}{8},\frac{1}{4},\frac{1}{16}$$ 中间状态概率显然高于两边。

    这样，在主成分的考虑中，中间状态可能是属于没有变化；其邻近状态时中度上升或下降；最边上的状态也许是极度上升和下降。鉴于第一主成分比第二主成分要重要很多，且第二主成分比第三主成分重要，第一主成分的状态需要比第二的多，而第二的比第三的多。一个常用的分配是7,5,3，概率为

    $$P(component1=i)\times P(component2=j)\times P(component3=k)$$

    $$=[2^{-m_1}\frac{m_1!}{i!(m_1-i)!}]\times [2^{-m_2}\frac{m_2!}{j!(m_2-j)!}]\times [2^{-m_3}\frac{m_3!}{k!(m_3-k)!}]$$

    然后，我们可以从这个概率分布中随机抽取场景，每个场景将会给出一个即期利率曲线和投资组合的收益损失。

  • 固收类VaR和ETL

    固收类产品属于对利率比较敏感的投资工具，包括债券、浮动利率票据、结构性票据和利率置换等利率衍生品。好消息是模拟技术比较适合于固收产品，在采用模拟技术来估算固收产品的VaR和ETL时，需要考虑两个比较关键的因素：利率的随机过程和期限结构。

    • 利率的随机过程

      与股票价格的随机过程不同，利率通常呈现出均值反转，最流行的利率随机过程是Cox–Ingersoll–Ross (CIR) 过程:

      $$dr=k(\mu -r)dt+\sigma \sqrt{dt}\sqrt{r}dz$$ ，$\mu$ 是长期利率均值，$\sigma$ 是利率年化波动率，$k$ 是利率反转到均值的速度，$dz$ 是一个标准正态随机变量。这个模型捕捉了利率的三个经验特征：stochastic, positive, mean-reverting。

    • 期限结构

      利率的期限结构一般是比较棘手的，因为大多数固收头寸都包含多个远期会到期的支付，所以固收的估值需要我们考虑即期期限结构的多个不同时间点。

      从估算VaR的角度上看，这意味着我们需要在持有到期时的预期期限结构的信息。VaR值依赖收益损失，而收益损失(P/L)依赖在持有期间的价格变化，价格依赖到期的即期期限结构，所以我们需要一个预期的未来期限结构。

  • 动态投资组合策略下估算VaR和ETL

  • 模拟方法估算信用相关风险

  • 模拟方法估算保险风险

  • 模拟方法估算养老金风险

  Mapping positions to risk factor

  ​ 很多情况下，我们需要从一个投资组合中区别各个头寸和风险因子，简单来说就是我们会经常把n个头寸映射到m个风险因子且通常是基准风险因子。主要过程分为三步：

  1. 构造一系列基准或核心投资工具或因子，收集其波动率和相关性数据。

  2. 为每一个所持有的投资工具产生合成替代品，组成在核心工具的头寸。

  3. 对合成替代品估算VaR和ETL.

  • 选择核心工具

    通常的做法是选择代表持有投资工具的宽泛类型，例如主要货币市场、权益类、现金类等。众所周知的RiskMetrics采用了以下核心工具：

    1. 权益类：对每一种核心货币使用等量的权益指数类
    2. 固收类：有限制的多个给定的到期时间的现金流的联合
    3. 外汇：外汇头寸以确定数目的核心货币的相近量来代表，外汇远期以相等的固收类头寸来表示。
    4. 大宗商品：以一定量的所选择的交易的标准远期合同来代表。

  • 选择核心因子

    另一种方法是选择核心因子而不是投资工具，因子的确定可以通过PCA量化方法。如前所言，通常PCA在降维方面非常有效，几个因子就可以解释大部分波动性。

  • 头寸映射和VaR估算

    我们现在考虑如何映射和估算VaR到特定类型的头寸。

    1）基本构成要素

    • 基本外汇头寸

      $$Va{R}^{FX}=-{\alpha }_{cl}{\sigma }_{E}xE$$

      这里，$x$是头寸价值，$E$ 为汇率，${\sigma }_E$ 为汇率标准差（认为汇率成正态分布）

    • 基本权益头寸

      令市场收益为 $R_m$ ,公司股票收益为 $R_A$ ,$\beta$ 收益为 ${\beta }_A$ , $\alpha$ 收益为 ${\alpha }_A$ ,

      有 $R_A={\alpha }_A+{\beta }_A{R}_m+{ϵ}_A$,

      收益方差为 ${\sigma }_A^2={\beta }_A^2{\sigma }_m^2+{\sigma }_{ϵ}^2$ ,

      假设收益为正态分布，$Va{R}_A=-{\alpha }_{cl}{\sigma }_A{x}_A=-{\alpha }_{cl}{x}_A\sqrt{{\beta }_A^2{\sigma }_m^2+{\sigma }_E^2}$

    • 零息债卷

      ​ 我们的任务是把无违约风险的零息债卷映射到参考投资工具上，例如月零息债券、3月零息债券等。我们会有这些特定到期时间债卷的波动率和相关性，但不包含其他到期时间的，所以我们没有我们所持有的特定到期时间零息债券的波动率和相关性数据。例如参考零息债券为30天和90天，我们所持有的债券是80天，我们该如何估算其VaR值呢？事实上，只能通过30天和90天的某种组合来估算。

      ​ 从RiskMetrics的建议上来看，映射后的头寸应该与原头寸有相同的价值和波动性，现金流应具备相同的符号。

      ​ 假设我们有一个6年的流入现金流，最近的参考到期时间工具为5年和7年，那么

      $$I_6^{mapped}=\omega I_5+(1-\omega )I_7$$

      $${\sigma }_6^2={\omega }^2{\sigma }_5^2+(1-\omega {)}^2{\sigma }_7^2+2\omega (1-\omega ){\rho }_{5,7}{\sigma }_5{\sigma }_7$$

      问题就转化为如何选择 $\omega$ , 其他项可知的情况下，我们可以解出

      $$\omega =[-b\pm \sqrt{b^2-4ac}]/2a$$

      $$a={\sigma }_5^2+{\sigma }_7^2-2{\rho }_{5,7}{\sigma }_5{\sigma }_7$$

      $$b=2{\rho }_{5,7}{\sigma }_5{\sigma }_7-2{\sigma }_7^2$$

      $$c={\sigma }_7^2-{\sigma }_6^2$$

    • 基本远期/期货

      假如我们有 $x$ 个价值为 $F$ 的远期或期货合同，

      $$VaR\approx -{\alpha }_{cl}{\sigma }_{F}xF$$

      如上面方法类似，四个月合同可以映射为不同参考到期时间的组合，

      $$I_4^{mapped}=\omega I_3+(1-\omega )I_6$$

  • 其他复杂的头寸

    • 带息债券
    • Forward Rate Agreements
    • Floating-rate instruments
    • Vanilla interest-rate swaps
    • Structural notes
    • FX forwords
    • Commodity, equity and FX swaps

Delta-Gamma and Related Approximations

​ 我们已经看到了采用线性方法把头寸映射到风险因子上，本小结讨论非线性方法。

​ 在处理期权和固收类时，这种非线性关系非常普遍。

• Delta-Normal 方法

  ​ 想象我们有股票看涨期权价值为 $c$, 价值依赖于很多底层因子，例如底层股票的价格、行权价格、价格波动率等。在Delta-Normal模型中，我们忽略除底层股票价格之外的其他因子，对期权价格变化采用一阶泰勒近似，

  $$\Delta c\approx \delta \Delta S$$， $\Delta c=c-\bar{c}$ , $\Delta S=S-\bar{S}$

  其中，$\delta$ 是期权的delta，带上划线的是该变量的当前值。

  当处理非常短的Holding Period时，

  $$Va{R}^{option}\approx \delta Va{R}^S\approx -\delta {\alpha }_{xl}\sigma S$$ , $\sigma$ 是 $S$ 的波动率

• Delta-Gamma方法

  ​ Delta-Gamma方法采用的是二阶泰勒近似，

  $$\Delta c\approx \delta \Delta S+(\gamma /2)(\Delta S{)}^2$$

• Delta-Gamma normal approach

  ​ 这种方法是把额外的风险项 $(\Delta S{)}^2$ 看成是一个独立的正态分布变量，

  $$\Delta c\approx \delta \Delta S+(\gamma /2)\Delta U$$

  把期权看成为两个正态风险因子的线性组合，其波动率为

  $${\sigma }_p=\sqrt{{\delta }^2{\sigma }^2+(\gamma /2{)}^2{\sigma }_U^2}=\sqrt{{\delta }^2{\sigma }^2+(1/4){\gamma }^2{\sigma }^4}$$

  $$Va{R}^{option}=-{\alpha }_{cl}{\sigma }_{p}S=-{\alpha }_{cl}\sigma S\sqrt{{\delta }^2+(1/4){\gamma }^2{\sigma }^2}$$

  ​ Delta-Gamma正态性方法通过把问题引回到线性正态领域而实现了可追溯性。但是这种方法存在一个逻辑问题，就是 $\Delta S$ 和 $(\Delta S{)}^2$ 不可能都是正态分布，如果 $\Delta S$ 是正态的，$(\Delta S{)}^2$ 应该是卡方分布。

• Wilson’s Delta-Gamma approach

Incremental and Component Risks

​ 这一节主要讨论加性风险和风险分解。当改变投资组合时，风险如何变化；如何分解组合风险？

• 增量风险(Incremental risks)

  当一些因子变化的时候，风险也会随之改变。例如说，我们想要知道但在组合中增加一个头寸时，VaR如何变化，这称为IVaR.

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3GDbraB7-1573309733306)(C:\Users\Martin\Documents\IVaR.PNG)]

  1. The Before and After Approach

  $$IVaR=VaR(p+a)-VaR(p)$$

  2. Garman’s ‘delVaR’ approach (Marginal VaRs)

  设投资组合 $p$ 有 $n$ 个映射头寸$[w_1,w_2,\cdots ,w_3]$ ，改变后的头寸大小为 $[w_1+\Delta w_1,\cdots ,w_n+\Delta w_n]$ ,采用一阶泰勒展开，

  $$VaR(p+a)\approx Var(p)+\sum _{i=1}^n\frac{\partial VaR}{\partial w_i}d{w}_i$$

  最后一项即为 $IVaR$ ，$d{w}_i\approx \Delta w_i$

  $$IVaR(a)\approx ▽VaR(p)dw$$

  当P/L为正态分布，且均值向量为 $\mu$ , 协方差矩阵为 $\Sigma$ 时，

  $$▽VaR(p)=-\mu +\frac{\Sigma w{\alpha }_{cl}}{[w^T\Sigma w{]}^{1/2}}$$

• 成分风险(component risks)

  对一定的整体风险而言，我们希望对风险进行分解，从而知道其风险成分都有什么。风险成分需要满足两个主要特性：Incrementality 和 Additivity。做风险分解时，首先我们需要选择分解的维度，例如投资工具、资产类别等。投资组合的VaR是一个线性齐次函数：$VaR=\sum_{i=1}^nw_i\frac{\partial VaR}{\partial w_i}=\bigtriangledown VaR§w $ ，我们定义工具 $i$ 的成分VaR，$CVa{R}_i=w_i\frac{\partial VaR}{\partial w_i}$ ，$VaR={\sum }_{i=1}^{n}CVa{R}_i$ .

  如果P/L为正态，$CVa{R}_i\approx {\omega }_i{\beta }_{i}VaR(p)$ ，这里 ${\omega }_i$ 为工具 $i$ 在整个组合中的比重，认为非常小；${\beta }_i$ 是工具 $i$ 在组合中的贝塔系数 ${\sigma }_{i,p}/{\sigma }_p^2$ ，${\sigma }_{i,p}$ 是工具 $i$ 与组合 $p$ 的收益协方差。

估算流动性风险

​ 本节讨论流动性问题和它是如何影响风险度量的，主要包含以下内容：

• 市场流动性和不流动性，以及其关联成本和风险。
• 在流动性和不流动性下估算VaR(LVaR, liquidity-adjust VaR)和ETL(LETL, liquidity-adjust ETL)。
• 度量在险流动性(LaR, Liquidity at Risk)
• 度量危机相关流动性风险(crisis-related liquidity risk)

1）流动性和流动性风险

​ 流动性是市场的功能，是执行交易或改变头寸，同时保持无成本，无风险，且具备便利性的能力。流动性依赖于市场中交易者的数量、交易频率、交易大小；交易时间和交易成本等多种因素。不同的交易工具具有不同的流动性成本和风险。

​ 第一个关心的问题使流动性问题如何影响VaR和ETL的估算，首先需要集中在流动性成本和流动性风险，因为它们与度量市场风险非常相关。流动性成本的主因是买卖价差(bid-ask spread)

2）交易成本估算法

$$TC=[1+PS/MS{]}^{{\lambda }_1}(AL\times spread/2)exp(-{\lambda }_{2}hp)$$

$$TC$$ 是交易成本，$PS$ 是头寸大小，$MS$ 是市场大小，$AL$ 是在持有期 $hp$ 结束时流动量，$spread$ 是买卖价差，${\lambda }_1$ 近似于交易成本的弹性，${\lambda }_2$ 近似于延迟率。

$$LVaR=VaR+TC$$ ,

可得 $LVaR=\frac{VaR+kPS}{1+k}$ ，$k=[1+PS/MS{]}^{{\lambda }_1}(spread/2)exp(-{\lambda }_{2}hp)$

$$\frac{LVaR}{VaR}=\frac{1+kPS/VaR}{1+k}$$

3）The Exogenous Spread Approach

​ 如果我们的头寸相对于市场非常小，我们可以认为流动性风险和我们的交易是无关的。假设价差具备均值 ${\mu }_{spread}$ ，标准差为 ${\sigma }_{spread}$ ，那么在 95% 的置信水平下，有

$$LVaR=[1+({\mu }_{spread}+1.645{\sigma }_{spread})/2]VaR$$

4）The Market Price Response Approach

​ 集中考虑交易对市场价格的影响。

5）Derivatives Pricing Approaches

​ 这种方法比较适合于流动性调整下的衍生品定价。

​ 我们定义流动性变量 $L$ 为底层资产价格 $S$ 对交易量 $N$ 的偏导的倒数，$L=1/(\partial S/\partial N)$ ，认为 $S$ 遵循以下过程：$dS=\mu dt+\sigma d{x}_t+\frac{1}{L}dN$ ，最后一项反映了顶层资产交易的影响。

​ 如果我们用Black-Shore等式建模，我们可以导出流动性调整后的等式，然后采用蒙特卡洛模拟来估算VaR和ETL.

6）The Liquidity Discount Approach

​ 流动性折损法有更为宽泛的应用且更为灵活，但它的要求也更多。考虑一个交易者，当他面临流动性优化问题时，他需要在一定的期间内流动其头寸，且最大化功效和寻找最好的方法。从三个方面来调整VaR：优化持有期、增加平均流动折损、增加流动时间波动和折损因子波动。

​ 流动性折损被表示称为一个比例因子 $c(s)$ ，$s$ 为交易量，

$$LVaR=-\mu hp-{\mu }_{logc(s)}-{\alpha }_{cl}\sigma \sqrt{hp}+2{\sigma }_{logc(s)}$$

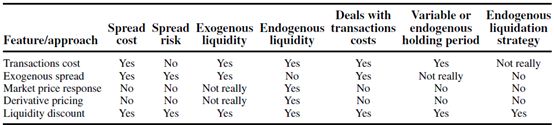
7）Summary and Comparison

估算在险流动性(LaR)

​ LaR有时也称为在险现金流(cash flow at risk)，为在一定期间内和在给定的置信区间最可能的流出现金流，它与流动性相关损失所带来的风险不同。LaR对很多因子都很敏感，包括：

• 借贷
• 保证金
• 附带义务
• 期权执行时触发的非预期现金流
• 风险管理策略变化

估算危机中的流动性

​ 我们现在考虑在危机情况下的流动性。在危机发生的时候，很多金融资产都会迅速贬值，出现重大损失和高买卖价差。

​ 假如我们持有一个单一的衍生品工具头寸，其P/L是一个delta-gamma近似，

$$\Pi =\delta dS+0.5\gamma (dS{)}^2$$ ，$dS$ 是股票价格的变化，最大损失出现的条件是 $dS=-\gamma /\delta$

得到 $L^{max}=-{\Pi }^{min}={\delta }^2/(2\gamma )$ ，最坏情况下的现金流出为 $m{\delta }^2/(2\gamma )$ ，$m$ 是保证金和附带责任。

​ 实际上，上述方法还是过于简单了，还应该考虑信用事件与市场风险因子的交互影响。

回测市场风险

​ 在我们确信我们的模型之前，我们需要验证其准确性；模型验证的关键问题是回测，回测是一种量化应用，通常采用统计方法来检验模型的风险估算是否与模型的假设是一致的。回测是风险度量过程的关键步骤，我们依赖其给出模型存在问题的指示。

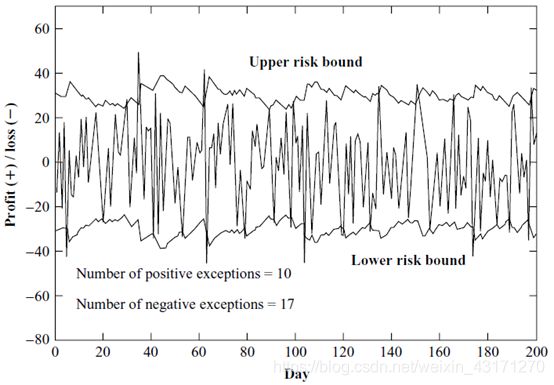
​ A backtesting chart

​ 上图是一个假设组合的日P/L序列，在5%到95%的置信水平下，预期有10个正向意外点和10个负向意外点，我们实际观察到了10个正向意外点和17个负向意外点。

• STATISTICAL BACKTESTS BASED ON THE FREQUENCY OF TAIL LOSSES

  所有统计检验的基本思想都是先选择显著性水平，然后假设原假设为真的情况下估算概率。

  1）The Basic Frequency-of-tail-losses (or Kupiec) Test

  这大概是最为广泛使用的尾部损失频率检验法，其主要思想是检验观察到的尾部损失频率(超过VaR的损失频率)与模型预测的频率是否一致。原假设为"The model is good"，尾部损失的数量 $x$ 服从二项式分布，

  $$Prob(x|n.p)=(\genfrac{}{}{0ex}{}{n}{i})p^i(1-p{)}^{n-i}$$ ，$n$ 为P/L的观测值的数量，$p$ 为尾部损失的预测频率，等于1-VaR的置信水平。

  2）The Time-to-first-tail-loss Test

  如果尾部损失的概率为 $p$ ，在期间 $T$ 内观测到第一次尾部损失的概率为 $p(1-p{)}^{T-1}$ ，截至到期间 $T$ 观测到第一次尾部损失的概率为 $1-(1-p{)}^T$ ，服从几何分布

  
  3）A Tail-Loss Confidence-interval Test

  这种方法是用来估算尾部损失的次数的置信区间，基于可用样本，它检查尾部损失的次数的期望值是否在样本中。

  4）The Conditional Backtesting (Christoffersen) Approach

  这种方法的主要思想是分离特别的假设，对分离后的假设分别做检验。

• STATISTICAL BACKTESTS BASED ON THE SIZES OF TAIL LOSSES

  前面的统计检验法主要考虑尾部风险发生的次数，但实际上损失的多少也是非常有用的信息。这一点对模型的完备性非常重要。

  1）The Basic Sizes-of-tail-losses Test

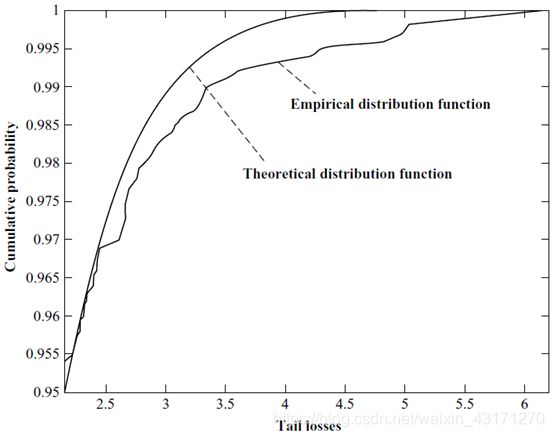
  首先估算VaR，然后对P/L数据值取负数从而使损失为正，只保留损失高于VaR的数据；这样得到了尾部损失观测值的经验分布。接下来我们用模型来预测此分布，然后比较两个分布的差，通常采用K-S检验。

  

  2）The Crnkovic–Drachman Backtest Procedure

  这种方法的关键是通过比较P/L的经验分布和预测分布的差异来评价模型，跨越其整个值域。每一个P/L观测值可以被分类成预测分布的分位数，如果模型是良好的，所分类的P/L观测值应该呈现均匀分布且是独立的。这种推理导出了两种检验：

  • 均匀分布检验
  • 标准独立检验(BDS test)

  3）The Berkowitz Approach

  CD方法告诉我们分类的P/L观测值应该服从 $iidU(0,1)$ ，我们可以在原假设下将其转化为正态分布：

  ​ 如果 $x_t\sim iidU(0,1)$ , 那么 $z_t={\Phi }^{-1}(x)$ 为 $iidN(0,1)$

  在正态分布下，我们可以使用更多的统计方法来进行检验。

• FORECAST EVALUATION APPROACHES TO BACKTESTING

  这一类方法允许我们对模型进行分级，但是并不提供任何关于模型完备性的统计指示。在分级中，它也允许我们考虑任何其他的特殊因素，例如我们会更加关心高额损失，因此希望给高额损失更大的权重。

  预测评估过程有四个要素、一个输出和对每一个模型的最终评分。

  四个要素为：

  1. $n$ 个成对观测值的集合(每一段期间的P/L和其关联的预测VaR)

  2. 损失函数：给每一个观测一个分数用来衡量其对比于VaR预测的观测损失。

     如果 $L_t$ 为在期间 $t$ 的损失或者盈利，损失函数为

     if $L_t>Va{R}_t$ ，$C_t=f(L_t,Va{R}_t)$

     else, $C_t=g(L_t,Va{R}_t)$

  3. 基准：一个良好模型的期望分数

  4. 评分函数：$QPS=(2/n){\sum }_{t=1}^n(C_t-p{)}^2$， $QPSin[0,2]$

  1）The Frequency-of-tail-losses (Lopez I) Approach

  Binominal Loss Function

  ​ if $L_t>Va{R}_t$ ，$C_t=1$

  ​ else, $C_t=0$

  ​ 基准 $p=E(C_t)$

  2）The Size-adjusted Frequency (Lopez II) Approach

  if $L_t>Va{R}_t$ ，$C_t=1+（L_t-Va{R}_t{)}^2$

  else, $C_t=0$

  基准估算通过蒙特卡洛模拟

  3）The Blanco-Ihle Approach

  ​ 基于前面方法中金额的平方项并没有很好的解释，

  ​ if $L_t>Va{R}_t$ ，$C_t=(L_t-Va{R}_t)/Va{R}_t$

  ​ else, $C_t=0$

  ​ 基准为 $\frac{ETL-VaR}{VaR}$

  4）An Alternative Sizes-of-tail-losses Approach

  ​ if $L_t>Va{R}_t$ ，$C_t=L_t$

  ​ else, $C_t=0$

  ​ 二次评分函数：$QS=(2/n){\sum }_{t=1}^n(C_t-ET{L}_t{)}^2$

  ​ 基准为ETL

• ASSESSING THE ACCURACY OF BACKTEST RESULTS

  标准的统计回测方法非常依赖于一个估算的概率值，毕竟其真实概率无从得知。所以，我们需要知道所估算概率值的精确度。

• BACKTESTING WITH ALTERNATIVE CONFIDENCE LEVELS, POSITIONS AND DATA

  

压力测试

​ 压力测试是用来判定投资组合对于假设事件的脆弱程度的标准步骤。长久以来，金融机构一直在使用压力测试，特别是在判定其利率风险敞口。压力测试比较适合于在危机情况下量化我们可能的损失，当危机出现时，正常的市场关系被打破，而VaR和ETL都带有误导性。

​ 压力测试可以确定我们的脆弱程度在不同的危机场景下，

• 正常相关关系被打破

• 突然的流动性下降

• 集中风险

• 宏观经济风险

  压力测试主要有两类方式，

1. 场景分析

模拟场景来评价模型。

2. 机械化压力测试

评价一系列统计可能性下的模型表现

模型风险

​ 金融模型是规范框架，可以使我们确定输出的价值，例如资产价格、对冲比率、VaR等。模型主要有三类：基础的、描述性的、和统计模型。

​ 模型是对真实世界高度简化抽象的结构，我们不应该期望模型可以给出完美的结果。模型必定会存在一定程度的错误，我们可以把这种错误的风险称为模型风险。需要注意的是并不是所有模型的输出错误都是模型风险。

​ 金融模型的最主要的输出就是价格，例如期权定价模型中的期权价格，Greek hedge ratio, options delta/gamma，或者风险度量中的VaR和ETL。无论任何模型都会有价格上的某种错误，事实上模型风险总会归于价格风险。

• SOURCES OF MODEL RISK

  1）Incorrect Model Specification

  Stochastic processes might be misspecified

  Missing risk factors

  Misspecified relationships

  Transactions costs and liquidity factors

  2）Incorrect Model Application

  当一个良好的模型被错误应用时也会产生模型风险。

  3）Implementation Risk

  模型的实现方式也会产生模型风险

  4）Other Sources of Model Risk

  Incorrect Calibration

  Programming Problems

  Data Problems

• COMBATING MODEL RISK

  模型风险并不能被完全消除，但是可以在一定程度上缩减。

  1）Some Guidelines for Risk Practitioners

  Be aware of model risk

  Identify, evaluate and check key assumptions

  Test models against known problems

  Choose the simplest reasonable model

  Backtest and stress test the model

  Estimate model risk quantitatively

  Don’t ignore small problems

  Plot results and use non-parametric statistics

  Re-evaluate models periodically

  2）Some Guidelines for Managers

  Pay attention to warning signals
  Ensure that their risk control systems are working

  3）Institutional Methods to Combat Model Risk

  Procedures to Vet, Check and Review Models

  Independent Risk Oversight