深度学习：基于python第6章 与学习相关的技巧

第6章 与学习相关的技巧

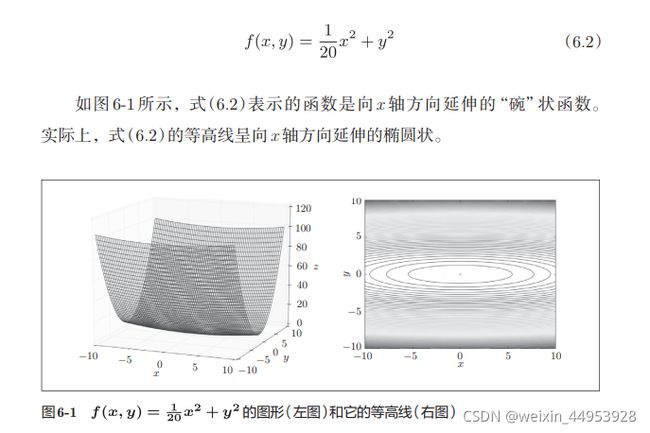
本章将介绍神经网络的学习中的一些重要观点，主题涉及寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法等。

为了 应对过拟合，本章还将介绍权值衰减、Dropout等正则化方法，并进行实现。

6.1 参数的更新

神经网络的学习的目的是找到使损失函数的值尽可能小的参数。

随机梯度下降法（stochastic gradient descent）， 简称 SGD

6.1.2　SGD

我们将SGD实现为一个Python类（为方便 后面使用，我们将其实现为一个名为SGD的类）

class SGD:
     def __init__(self, lr=0.01):
     	self.lr = lr3
        
     def update(self, params, grads):
         for key in params.keys():
        	 params[key] -= self.lr * grads[key]

参数params和grads（与之前的神经网络 的实现一样）是字典型变量，按params[‘W1’]、grads[‘W1’]的形式，分别保 存了权重参数和它们的梯度。

使用这个SGD类，可以按如下方式进行神经网络的参数的更新（下面的 代码是不能实际运行的伪代码）

network = TwoLayerNet(...)
optimizer = SGD()

for i in range(10000):
     ...
     x_batch, t_batch = get_mini_batch(...)    # mini-batch
     grads = network.gradient(x_batch, t_batch)
     params = network.params
     optimizer.update(params, grads)
     ...

变量名optimizer表示“进行最优化的人”的意思。参数的更新由optimizer负责完成。

6.1.3　SGD的缺点

SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索 的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的SGD更聪 明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。

6.1.4　Momentum

class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {
     }
            for key, val in params.items():   #items():遍历字典中所有的key 以及value                             
                self.v[key] = np.zeros_like(val) #生成和val一样形状，值全为0的
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] #刚开始0-m=负数，然后负数减负数
            params[key] += self.v[key]

初始化时，v中什么都不保存，但当第 一次调用update()时，v会以字典型变量的形式保存与参数结构相同的数据。

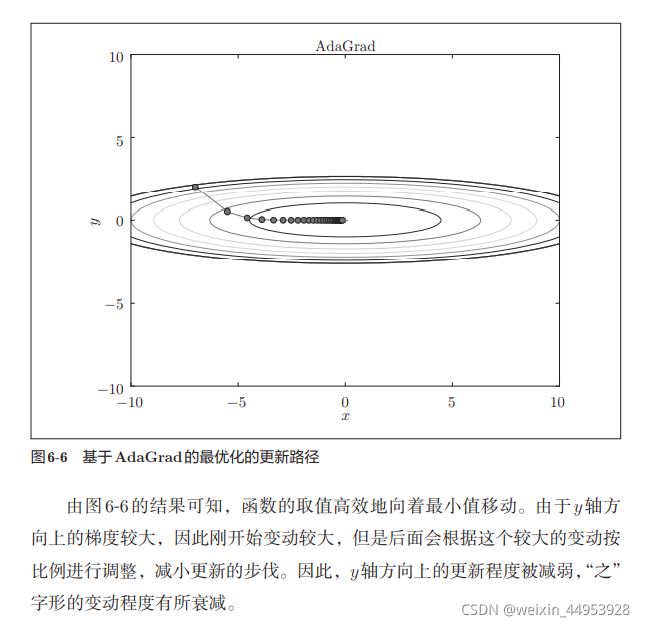
6.1.5　AdaGrad

在神经网络的学习中，学习率（数学式中记为η）的值很重要。学习率过小， 会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能 正确进行。

有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多” 学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用

class AdaGrad:

    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {
     }
            for key, val in params.items():     #items():遍历字典中所有的key 以及value   
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

这里需要注意的是，最后一行加上了微小值1e-7。这是为了防止当 self.h[key]中有0时，将0用作除数的情况。

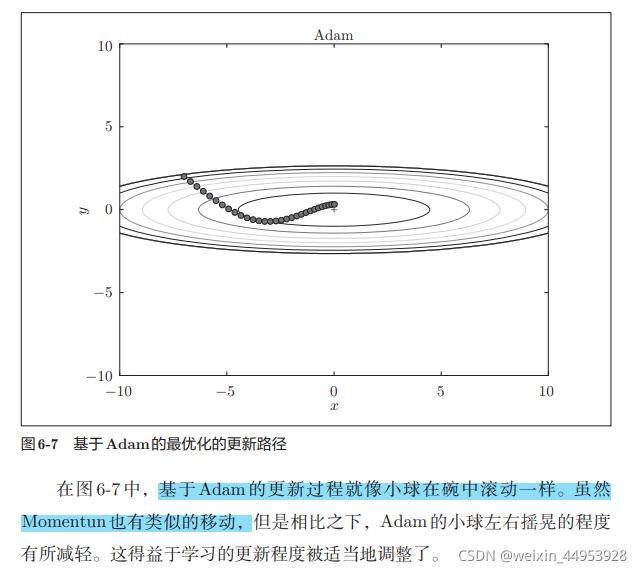
6.1.6　Adam

Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参 数的每个元素适当地调整更新步伐。如果将这两个方法融合在一起会怎么样 这就是Adam[8]方法的基本思路.

class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):  #beta1=0.9, beta2=0.999 是同 momentum=0.9一样
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {
     }, {
     }
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

6.1.7　使用哪种更新方法呢

学习了4种更新参数的方法

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
from common.optimizer import *


def f(x, y):
    return x**2 / 20.0 + y**2


def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {
     }
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {
     }
grads['x'], grads['y'] = 0, 0


optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
    

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)
    
    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
    
plt.show()

6.1.8　基于MNIST数据集的更新方法的比较

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
optimizers = {
     }
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {
     }
train_loss = {
     }
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.绘制图形==========
markers = {
     "SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()